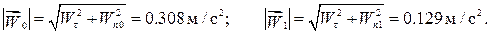Подобным образом можно определить положение точки, ее скорость и ускорение в заданный момент времени при любых других заданных кинематических уравнениях движения точки в декартовой системе координат.

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 10.2; 10.12; 10.14; 12.22; 12.23.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-16.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2

1.2. Естественный способ задания движения точки

Пример 1.4

Точка движется по окружности радиуса 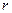. Начало и направление отсчета дуговой координаты указаны на Рис. 1.4. Закон изменения дуговой координаты имеет вид:

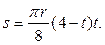
Определить траекторию точки при 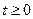, а также положение, скорость и ускорение точки в конце первой и пятой секунд движения.

Чтобы определить траекторию точки, проведем анализ ее движения. Вычислим проекцию скорости на касательную и касательное ускорение:

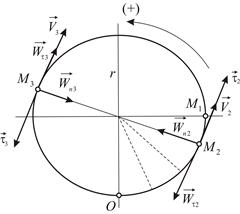Рис. 1.4

Как видно, касательное ускорение точки не зависит от времени, т.е. движение точки равнопеременное. В начальный момент времени

при

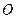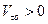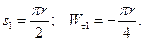Следовательно, точка начинает движение из начала отсчета в положительном направлении, поскольку, . Напомним, что единичный вектор касательной всегда направлен в сторону возрастания дуговой координаты. Точка может поменять направление движения на противоположное только после остановки. При В этот момент времени Следовательно, к моменту времени 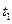точка прошла в положительном направлении четверть длины окружности и находится в положении .

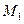Возникает вопрос о направлении дальнейшего движения точки. Поскольку скорость обратилась в нуль, о направлении движения можно судить по направлению касательной составляющей ускорения. Касательное ускорение в точке остановки отрицательно и, следовательно, точка начнет движение в отрицательном направлении отсчета. Других точек остановок нет. Поэтому точка не будет больше менять направление движения. Со временем она будет описывать окружность, проходя ее в отрицательном направлении, по ходу часовой стрелки.

Для заданного момента времени получаем:

для заданного момента времени получаем:

Полученные результаты изображены на чертеже. Заметим, что, прежде всего, необходимо изобразить единичный вектор касательной 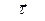в данной точке, с направлением которого необходимо согласовывать направления векторов 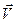и .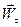

Траекторией точки в интервале времени 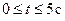является дуга 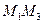нижней части окружности.

Пример 1.5

Даны законы движения точки в координатной форме:

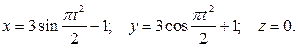
Определить траекторию точки при 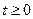и закон движения точки по траектории.

Исключая время из законов движения, получаем:

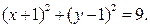
Из уравнений движения следуют ограничения на область значений координат в интервале времени :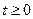

Таким образом, траекторией точки является вся окружность радиуса 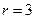с центром в точке 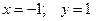(Рис. 1.5).

Начало отсчета дуговой координаты совместим с начальным положением точки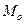

при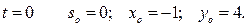

Положительное направление отсчета дуговой координаты 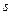совместим с направлением, в котором точка начинает движение. Вычислим проекции скорости на координатные оси

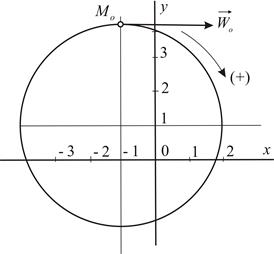Рис.1.5

Как видно, при 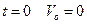, так что для определения направления движения необходимо вычислить ускорение точки

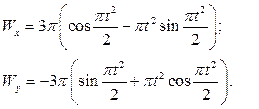
В начальный момент, т.е. при 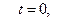получаем: 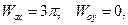так что точка начинает обход окружности по ходу часовой стрелки. В этом направлении и будем откладывать положительные дуговые координаты.

Определим модуль скорости

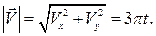
Как видно, скорость точки не обращается в нуль ни при каких значениях времени . Поэтому полагаем

Найдём закон изменения дуговой координаты:

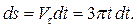
Интегрируя последнее равенство, получаем:

Пример 1.6

Поезд движется равно замедленно по дуге окружности радиуса 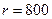м и проходит путь м, имея начальную скорость км/час и конечную км/час. Определить полное ускорение поезда в начале и конце дуги, а также время 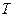движения поезда по этой дуге.

По условию движение равнопеременное. Законы равнопеременного движения имеют вид:

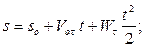
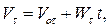
Запишем эти соотношения для момента времени 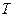, учитывая что :

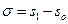Решая полученную систему уравнений, находим

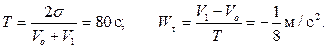
Найдем нормальное ускорение в начальной и конечной точках:

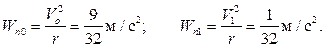
Для вычисления модуля ускорения воспользуемся тем обстоятельством, что касательная и нормальная составляющие ускорения взаимно перпендикулярны: