Механические свойства твердых тел и их показатели

Механическими свойствамитвердого тела называются его специфические признаки, проявляющиеся при механических процессах и обусловленные природой и внутренним строением тела.

Все твердые тела в зависимости от диапазона нагружения и внешних условий в большей или меньшей степени проявляют свойства:

· упругости – способности тела накапливать исчезающую при разгрузке деформацию;

· пластичности – способности тела накапливать не исчезающую при разгрузке деформацию;

· вязкости – способности тела накапливать деформацию во времени при постоянном напряжении;

Упругость и пластичность относятся к мгновенным свойствам тела, а вязкость – к его временным свойствам.

Обычно для изучения всех этих свойств и определения состояния тел на грани разрушения проводят простые опыты: осевое растяжение, сжатие, изгиб, сдвиг (срез или кручение) цилиндрических или призматических образцов в соответствии с методиками и определенными стандартами.

По данным этих опытов строятся деформационные кривые, устанавливающие связь между соответствующими компонентами напряжений 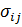, деформаций 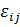, скоростей деформации 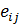и времени

Кроме того, определяют параметры предельного состояния, характеризующие разрушение материала. Все это служит основной выбора определяющих математических моделей деформирования и разрушения твердых тел.

Пример

На примере кратковременного растяжения (сжатия) цилиндрического образца легко проследить характерные мгновенные свойства твердых тел. На рис. 6.1 показан общий вид деформационной кривой напряжение-деформация ( ).

Эта кривая разбита на следующие характерные участки:

- ОА – участок упругих деформаций, где материал подчиняется линейному закону Гука:

где 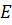- модуль упругости (модуль Юнга);

Рисунок 6.1 – Общий вид деформационной кривой

- АВ –участок пластического течения (или текучести), характеризуемый нарастанием деформации при неизменном напряжении , которое называется пределом упругости или пределом текучести;

- ВС – участок упрочнения, где нелинейная зависимость между напряжением и деформацией представлена в виде:

,

где - модуль пластичности;

- CD – участок разрушения, напряжение называется пределом прочности;

- LM – участок разгрузки или повторной нагрузки.

Если точка L расположена выше точки A, то при полной разгрузке исчезает накопленная упругая деформация и сохраняется деформация пластическая .

При повторном нагружении образца его диаграмма мало отличается от кривой MLC, т.е. материал в результате первоначального нагружения выше как бы приобретает дополнительные упругие свойства и повышает предел упругости . Это явление называется упрочнением.

Для определения модуля пластичности используют следующий степенной закон:

,

где и 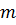– константы материала при испытаниях в заданных условиях.

При осевом нагружении цилиндрического образца изменяется и его поперечный размер, определяемый деформацией .

Величина 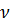, равная отношению абсолютных значений поперечной деформации к продольной в упругой области при осевом нагружении образца, называется коэффициентом Пуассона.

Способность твердых тел сжиматься или расширяться устанавливается диаграммой всестороннее давление – объемная деформация ( ):

где - модуль объемного сжатия (расширения) в зависимости от вида нагружения.

Определение модуля эквивалентно определению коэффициента Пуассона 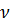, так как они связаны зависимостью

Для реальных тел коэффициент Пуассона не может превосходить значения 0,5, т.е. .

Если для какого-либо тела можно принять 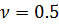, то такое идеальное тело принято называть несжимаемым, так как .

Деформационная кривая может иметь разнообразный вид в зависимости от свойств материала и внешних условий. По этой кривой находят не только основные механические параметры тела, но и устанавливают определяющее его свойство – меру пластичности.