Материальная (индивидуальная, полная) производная по времени

Материальная или индивидуальная производная по времениот величины описывает, как меняется со временем величина в индивидуальной точке среды. Обычно в механике сплошных сред индивидуальная производная функции обозначается

Как вычисляется индивидуальная производная по , если задана по способу Лагранжа, то есть ? Так как для индивидуальной точки , , то очевидно, индивидуальная производная есть просто частная производная по времени :

(2.7)

Здесь символом обозначен набор .

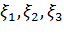Какие надо проводить измерения, чтобы найти индивидуальную производную по ? Надо иметь прибор, который следит за индивидуальной частицей, например, движется вместе с ней и измеряет в этой частице (рисунки 2.1 и 2.2). Для измерения величины индивидуальной производной в данной точке А в момент времени в той частице, которая находится в этот момент в точке А, затем в близкий момент измерить в той же самой индивидуальной частице (которая в этот момент находится уже не в точке А, а в точке В!) и разность полученных значений разделить на :

(2.8)

Рисунок 2.2 ­– Измерение значения индивидуальной производной в материальной точке

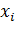Как вычисляется индивидуальная производная по , если задана по способу Эйлера, то есть ? Вычислим сначала частную производную по при постоянных , то есть величину . Что она описывает? Она описывает изменение со временем в фиксированной точке пространства; поэтому называется локальной производной по времени. Если среда движется, то в рассматриваемой точке пространства в разные моменты времени находятся разные индивидуальные точки среды. Приближенное значение в точке А измеряется так (рис. 2.3):

(2.9)

Рисунок 2.3 – Измерение значения локальной производной в точке А в момент времени

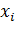Поэтому для индивидуальной точки является сложной функцией времени: зависит от , и , а 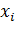зависят от и 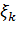, и индивидуальная производная вычисляется как производная сложной функции

Далее, производные по времени от координат 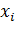при постоянных есть компоненты скорости частицы

.

(2.10)

Поэтому выражение для индивидуальной производной при эйлеровом описании таково

(2.11)

В последнем выражении использовано следующее соглашение о суммировании (правило Эйнштейна): если в одночлене какой-то индекс повторяется дважды, то по этому индексу производится суммирование от 1 до 3, а знак суммы не пишется, то есть

(2.12)

Отметим, что обозначение индекса суммирования при этом не существенно,

(2.13)

Линии тока и траектории

Понятие линий тока используется при эйлеровом описании движения среды, в основном при описании движения жидкостей и газов.

Линия тока - это линия, которая определяется для фиксированного момента времени и обладает тем свойством, что в каждой ее точке направление касательной совпадает с направлением вектора скорости среды. Отметим, что в рассматриваемый момент времени в разных точках линии тока находятся разные частицы.

Понятие траектории связано с лагранжевым подходом к описанию движения.

Траектория – это путь индивидуальной частицы; в каждой точке траектории направление касательной к траектории совпадает с направлением вектора скорости. Но здесь имеется в виду скорости одной и той же частицы в разные моменты времени, в то время как, говоря о линии тока, мы рассматриваем скорости разных частиц в один и тот же момент времени.

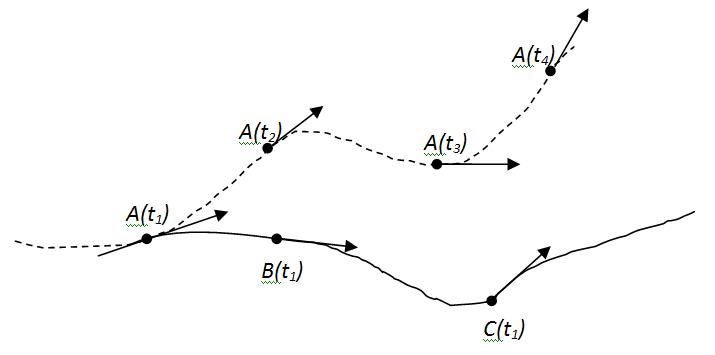
Рисунок 2.5 – Сплошная линия – линия тока в момент времени 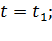пунктир – траектория точки А