Приложения – статистические таблицы

Приложение 1. Значения интеграла Лапласа

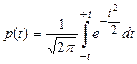
t	Сотые доли
0,00	0,0000	0,0080	0,0160	0,0239	0,0319	0,0399	0,0478	0,0558	0,0638	0,0717
0,10	0,0797	0,0876	0,0955	0,1034	0,1113	0,1192	0,1271	0,1350	0,1428	0,1507
0,20	0,1585	0,1663	0,1741	0,1819	0,1897	0,1974	0,2051	0,2128	0,2205	0,2282
0,30	0,2358	0,2434	0,2510	0,2586	0,2661	0,2737	0,2812	0,2886	0,2961	0,3035
0,40	0,3108	0,3182	0,3255	0,3328	0,3401	0,3473	0,3545	0,3616	0,3688	0,3759
0,50	0,3829	0,3899	0,3969	0,4039	0,4108	0,4177	0,4245	0,4313	0,4381	0,4448
0,60	0,4515	0,4581	0,4647	0,4713	0,4778	0,4843	0,4907	0,4971	0,5035	0,5098
0,70	0,5161	0,5223	0,5285	0,5346	0,5407	0,5467	0,5527	0,5587	0,5646	0,5705
0,80	0,5763	0,5821	0,5878	0,5935	0,5991	0,6047	0,6102	0,6157	0,6211	0,6265
0,90	0,6319	0,6372	0,6424	0,6476	0,6528	0,6579	0,6629	0,6680	0,6729	0,6778
1,00	0,6827	0,6875	0,6923	0,6970	0,7017	0,7063	0,7109	0,7154	0,7199	0,7243
1,10	0,7287	0,7330	0,7373	0,7415	0,7457	0,7499	0,7540	0,7580	0,7620	0,7660
1,20	0,7699	0,7737	0,7775	0,7813	0,7850	0,7887	0,7923	0,7959	0,7995	0,8029
1,30	0,8064	0,8098	0,8132	0,8165	0,8198	0,8230	0,8262	0,8293	0,8324	0,8355
1,40	0,8385	0,8415	0,8444	0,8473	0,8501	0,8529	0,8557	0,8584	0,8611	0,8638
1,50	0,8664	0,8690	0,8715	0,8740	0,8764	0,8789	0,8812	0,8836	0,8859	0,8882
1,60	0,8904	0,8926	0,8948	0,8969	0,8990	0,9011	0,9031	0,9051	0,9070	0,9090
1,70	0,9109	0,9127	0,9146	0,9164	0,9181	0,9199	0,9216	0,9233	0,9249	0,9265
1,80	0,9281	0,9297	0,9312	0,9328	0,9342	0,9357	0,9371	0,9385	0,9399	0,9412
1,90	0,9426	0,9439	0,9451	0,9464	0,9476	0,9488	0,9500	0,9512	0,9523	0,9534
2,00	0,9545	0,9556	0,9566	0,9576	0,9586	0,9596	0,9606	0,9615	0,9625	0,9634
2,10	0,9643	0,9651	0,9660	0,9668	0,9676	0,9684	0,9692	0,9700	0,9707	0,9715
2,20	0,9722	0,9729	0,9736	0,9743	0,9749	0,9756	0,9762	0,9768	0,9774	0,9780
2,30	0,9786	0,9791	0,9797	0,9802	0,9807	0,9812	0,9817	0,9822	0,9827	0,9832
2,40	0,9836	0,9840	0,9845	0,9849	0,9853	0,9857	0,9861	0,9865	0,9869	0,9872
2,50	0,9876	0,9879	0,9883	0,9886	0,9889	0,9892	0,9895	0,9898	0,9901	0,9904
2,60	0,9907	0,9909	0,9912	0,9915	0,9917	0,9920	0,9922	0,9924	0,9926	0,9929
2,70	0,9931	0,9933	0,9935	0,9937	0,9939	0,9940	0,9942	0,9944	0,9946	0,9947
2,80	0,9949	0,9950	0,9952	0,9953	0,9955	0,9956	0,9958	0,9959	0,9960	0,9961
2,90	0,9963	0,9964	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972
3,00	0,9973	0,9974	0,9975	0,9976	0,9976	0,9977	0,9978	0,9979	0,9979	0,9980
3,10	0,9981	0,9981	0,9982	0,9983	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986
3,20	0,9986	0,9987	0,9987	0,9988	0,9988	0,9988	0,9989	0,9989	0,9990	0,9990
3,30	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
3,40	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995	0,9995
3,50	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997	0,9997

Приложение 2. Значения t-критерия Стьюдента

при уровне значимости a: 0,10, 0,05, 0,01

Число степеней свободы ν	a	Число степеней свободы ν	a
0,1	0,05	0,01	0,1	0,05	0,01
	6,314	12,706	63,66		1,734	2,101	2,878
	2,92	4,3027	9,925		1,729	2,093	2,861
	2,353	3,1825	5,841		1,725	2,086	2,845
	2,132	2,7764	4,604		1,721	2,08	2,831
	2,015	2,5706	4,032		1,717	2,074	2,819
	1,943	2,4469	3,707		1,714	2,069	2,807
	1,895	2,3646	3,5		1,711	2,064	2,797
	1,86	2,306	3,355		1,708	2,06	2,787
	1,833	2,2622	3,25		1,706	2,056	2,779
	1,813	2,2281	3,169		1,703	2,052	2,771
	1,796	2,201	3,106		1,701	2,048	2,763
	1,782	2,1788	3,055		1,699	2,045	2,756
	1,771	2,1604	3,012		1,697	2,042	2,75
	1,761	2,1448	2,977		1,684	2,021	2,705
	1,753	2,1315	2,947		1,671		2,66
	1,746	2,1199,	2,921		1,658	1,98	2,617
	1,74	2,1098	2,898		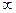1,645	1,96	2,576

Приложение 3. Значения χ²-критерия Пирсона

α ν	0,10	0,05	0,025	0,01	0,005
	2,7055	3,8415	5,0239	6,6349	7,8794
	4,6052	5,9915	7,3778	9,2103	10,5966
	6,2514	7,8147	9,3484	11,3449	12,8382
	7,7794	9,4877	11,1433	13,2767	14,8603
	9,2364	11,0705	12,8325	15,0863	16,7496
	10,6446	12,5916	14,4494	16,8119	18,5476
	12,0170	14,0671	16,0128	18,4753	20,2777
	13,3616	15,5073	17,5346	20,0902	21,9550
	14,6837	16,9190	19,0228	21,6660	23,5894
	15,9872	18,3070	20,4832	23,2093	25,1882
	17,2750	19,6751	21,9201	24,7250	26,7569
	18,5494	21,0261	23,3367	26,2170	28,2995
	19,8119	22,3620	24,7356	27,6883	29,8195
	21,0641	23,6848	26,1190	29,1412	31,3194
	22,3071	24,9958	27,4884	30,5779	32,8013
	23,5418	26,2962	28,8454	31,9999	34,2672
	24,7690	27,5871	30,1910	33,4087	35,7185
	25,9894	28,8693	31,5264	34,8053	37,1565
	27,2036	30,1435	32,8523	36,1909	38,5823
	28,4120	31,4104	34,1696	37,5662	39,9969
	29,6151	32,6706	35,4789	38,9322	41,4011
	30,8133	33,9244	36,7807	40,2894	42,7957
	32,0069	35,1725	38,0756	41,6384	44,1813
	33,1962	36,4150	39,3641	42,9798	45,5585
	34,3816	37,6525	40,6465	44,3141	46,9279
	35,5632	38,8851	41,9232	45,6417	48,2899
	36,7412	40,1133	43,1945	46,9629	49,6449
	37,9159	41,3371	44,4608	48,2782	50,9934
	39,0875	42,5570	45,7223	49,5879	52,3356
	40,2560	43,7730	46,9792	50,8922	53,6720

Приложение 4. Значения F-критерия Фишера

при уровне значимости a = 0,05

ν1 ν2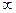
	161,5		215,7	224,6	230,2		238,9	243,9		254,3
	18,5		19,16	19,25	19,3	19,33	19,37	19,41	19,45	19,5
	10,13	9,55	9,28	9,12	9,01	8,94	8,84	8,74	8,64	8,53
	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,77	5,63
	6,61	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,53	4,36
	5,99	5,14	4,76	4,53	4,39	4,28	4,15		3,84	3,67
	5,59	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,41	3,23
	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,12	2,93
	5,12	4,26	3,86	3,63	3,48	3,37	3,23	3,07	2,9	2,71
	4,96	4,1	3,71	3,48	3,33	3,22	3,07	2,91	2,74	2,54
	4,84	3,98	3,59	3,36	3,2	3,09	2,95	2,79	2,61	2,4
	4,75	3,88	3,49	3,26	3,11		2,85	2,69	2,5	2,3
	4,67	3,8	3,41	3,18	3,02	2,92	2,77	2,6	2,42	2,21
	4,6	3,74	3,34	3,11	2,96	2,85	2,7	2,53	2,35	2,13
	4,54	3,68	3,29	3,06	2,9	2,79	2,64	2,48	2,29	2,07
	4,49	3,63	3,24	3,01	2,85	2,74	2,59	2,42	2,24	2,01
	4,45	3,59	3,2	2,96	2,81	2,7	2,55	2,38	2,19	1,96
	4,41	3,55	3,16	2,93	2,77	2,66	2,51	2,34	2,15	1,92
	4,38	3,52	3,13	2,9	2,74	2,63	2,48	2,31	2,11	1,88
	4,35	3,49	3,1	2,87	2,71	2,6	2,45	2,28	2,08	1,84
	4,32	3,47	3,07	2,84	2,68	2,57	2,42	2,25	2,05	1,81
	4,3	3,44	3,05	2,82	2,66	2,55	2,4	2,23	2,03	1,78
	4,28	3,42	3,03	2,8	2,64	2,53	2,38	2,2		1,76
	4,26	3,4	3,01	2,78	2,62	2,51	2,36	2,18	1,98	1,73
	4,24	3,38	2,99	2,76	2,6	2,49	2,34	2,16	1,96	1,71
	4,22	3,37	2,98	2,74	2,59	2,47	2,32	2,15	1,95	1,69
	4,21	3,35	2,96	2,73	2,57	2,46	2,3	2,13	1,93	1,67
	4,2	3,34	2,95	2,71	2,56	2,44	2,29	2,12	1,91	1,65
	4,18	3,33	2,93	2,7	2,54	2,43	2,28	2,1	1,9	1,64
	4,17	3,32	2,92	2,69	2,53	2,42	2,27	2,09	1,89	1,62
	4,12	3,26	2,87	2,64	2,48	2,37	2,22	2,04	1,83	1,57
	4,08	3,23	2,84	2,61	2,45	2,34	2,18		1,79	1,52
	4,06	3,21	2,81	2,58	2,42	2,31	2,15	1,97	1,76	1,48
	4,03	3,18	2,79	2,56	2,4	2,29	2,13	1,95	1,72	1,44
		3,15	2,76	2,52	2,37	2,25	2,1	1,92	1,7	1,39
	3,98	3,13	2,74	2,5	2,35	2,23	2,07	1,89	1,67	1,35
	3,96	3,11	2,72	2,49	2,33	2,21	2,06	1,88	1,65	1,31
	3,95	3,1	2,71	2,47	2,32	2,2	2,04	1,86	1,64	1,28
	3,94	3,09	2,7	2,46	2,3	2,19	2,03	1,85	1,63	1,26
	3,92	3,07	2,68	2,44	2,29	2,17	2,01	1,83	1,6	1,21
	3,9	3,06	2,66	2,43	2,27	2,16		1,82	1,59	1,18
	3,89	3,04	2,65	2,42	2,26	2,14	1,98	1,8	1,57	1,14
	3,87	3,03	2,64	2,41	2,25	2,13	1,97	1,79.	1,55	1,1
	3,86	3,02	2,63	2,4	2,24	2,12	1,96	1,78	1,54	1,07
	3,86	3,01	2,62	2,39	2,23	2,11	1,96	1,77	1,54	1,06
	3,85		2,61	2,38	2,22	2,1	1,95	1,76	1,53	1,03
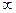	3,84	2,99	2,6	2,37	2,21	2,09	1,94	1,75	1,52

Приложение 5. Критические значения коэффициента автокорреляции

при уровне значимости α: 0,05 и 0,01

Объем выборки n	Положительные значения	Отрицательные значения
α = 0,05	α = 0,01	α = 0,05	α = 0,01
	0,253	0,297	-0,753	-0,798
	0,345	0,447	-0,708	-0,863
	0,370	0,510	-0,674	-0,799
	0,371	0,531	0,625	-0,764
	0,366	0,533	-0,593	-0,737
	0,360	0,525	-0,564	-0,705
	0,353	0,515	-0,539	-0,679
	0,348	0,505	-0,516	-0,655
	0,341	0,495	-0,497	-0,634
	0,335	0,485	-0,479	-0,615
	0,328	0,475	-0,462	-0,597
	0,299	0,432	-0,399	-0,524

Приложение 6. Значения критерия Колмогорова P(λ)

λ	P	λ	P
0,30		0,80	0,5441
0,35	0,9997	0,85	0,4653
0,40	0,9972	0,90	0,3927
0,45	0,9874	0,95	0,3275
0,50	0,9639	1,0	0,2700
0,55	0,9228	1,1	0,1777
0,60	0,8643	1,2	0,1122
0,65	0,7920	1,3	0,0681
0,70	0,7112	1,4	0,0397
0,75	0,6272	1,5	0,0222

[1] От лат. status – состояние, положение вещей; первоначально термин употреблялся в значении «политическое состояние»

[2] Эту деятельность на профессиональном уровне осуществляет государственная статистика – Федеральная служба государственной статистики (ФСГС) и система ее учреждений, организованных по административно-территориальному признаку, а также ведомственная статистика (на предприятиях, ведомствах, министерствах и т.д.). Информация ФСГС публикуется в специадльных печатных изданиях, а также в сети Интернет: www.gks.ru (или www.fsgs.ru)

[3] Термин «статистика» как параметр, как статистический критерий употребляется преимущественно в математической статистике, некоторые из них (χ², t и др.) рассмотрены в соответствующих темах данного курса лекций

[4] «There are three types of lies - lies, damn lies, and statistics» (Benjamin Disraeli, 1804 – 1881)

[5] « As a general rule, the most successful man in life is the man who has the best information »

[6] Аналогично общее количество школьных тетрадей измеряется в у.ш.т.(условные школьные тетради размером 12 листов), продукция кон­сервного производства измеряется в у.к.б. (условные консервные бан­ки емкостью 1/3 литра или 400 грамм); продукция моющих средств приво­дится к условной жирности 40%

[7] f – это начальная буква англ. слова frequency – частота

[8] В статистике, в отличие от математики, пределы суммирования не ставятся, а подразумеваются, так как абсолютные величины здесь не абстрактные, а смысловые (суммируются все величины совокупности – с первой по последнюю)

[9] Во многих учебниках по статистике встречается другое название индекса динамики – темп роста. Использование такого названия не совсем логично, так динамика может быть различна (не только рост, но и спад, а также стабильность), поэтому наиболее правильным является использование названия «индекс динамики» или «индекс изменения»

[10] Часто встречается и другое название темпа изменения – темп прироста, что не совсем логично (см. предыдущую сноску)

[11] Обычно (в т.ч. и в дальнейшем в данном пособии) в статистических формулах пределы суммирования не ставятся, а подразумеваются, т.е. подразумеваются именно такие пределы как формуле (11) – с 1-ой группы по N-ю (последнюю)

[12] Для взвешенной средней сумма взвешенных отклонений равна нулю – доказать самостоятельно

[13] Если приходится иметь дело с интервальным рядом распределения с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала, полученное значение называется плотностью ρ, то есть ρ = f/h

[14] Единицы совокупности, имеющие значение признака, равное границе интервала, включаются в тот интервал, где это точное значение впервые указывается

[15] От греч. «гистос» – ткань, строение

[16] От греч. слов «поли» и «гонос» – многоугольник

[17] При четном числе единиц совокупности за медиану принимают полусумму из двух центральных вариант

[18] Получите формулы и произведите их расчет (по аналогии с формулами для расчета квартилей) самостоятельно

[19] Максимально возможные значения показателей вариации: Л_max = ; ;;

[20] Например, цена продажи американского доллара в коммерческих банках Н.Новгорода 26 июля 2007 года варьировала от 25,45 до 26,00 при средней цене 25,595 руб., тогда по формуле (32) = (26,00–25,45)/25,595 = 0,021, или 2,1%. Такая малая вариация вызвана тем, что при значительном различии курса доллара немедленно произошел бы отлив покупателей из «дорогого» банка в более «дешевые». Напротив, цена килограмма говядины в разных регионах России варьирует очень сильно – на десятки процентов и более. Это объясняется разными затратами на доставку товара из региона-производителя в регион потребитель.

[21] Прочие виды распределений изучаются дисциплиной «Теория вероятностей»

[22] Простой расчет возможен при наличии Excel из пакета Microsoft Office, где имеется функция, вычисляющая плотность (или интеграл) функции нормального распределения =НОРМРАСП(А;Б;В;Г), где параметры: А – значение X; Б – средняя арифметическая ; В – среднее квадратическое отклонение σ; Г – «0» для вычисления плотности (или «1» для вычисления интеграла) распределения

[23] Иногда за счет округлений при расчетах (использование функции плотности распределения вместо интеграла) может быть нарушено равенство сумм эмпирических и теоретических частот, что и произошло в нашем примере про ВО (∑f=35, ∑m=33,832)

[24] Практически приемлемая вероятность в экономических исследованиях, означающая, что в 5 случаях из 100 может быть отвергнута правильная гипотеза

[25] Основное условие для использования критерия Колмогорова – достаточно большое число наблюдений (N > 50)

[26] Названо по имени французского математика Симеона Пуассона (1781 – 1840), еще называют законом распределения редких явлений; возникает, когда значения признака выражены дискретно и являются результатом какого-либо редко возникающего события среди наблюдаемых единиц, причем с увеличением значений признака вероятность наступления события падает

[27] Важно не путать понятие «структурный сдвиг», оцениваемый в теме 8, где он представляет не величину самого изменения структуры, а его влияние на результативный показатель

[28] Индекс не удовлетовряет свойству независимости от раскола совокупности

[29] Существуют и другие показатели, о которых можно прочитать в специальной литературе

[30] Приведены наиболее простые функции, более сложные виды, такие как логарифмическая, логистическая и др. описаны в специальной литературе, например – [2]

[31] При расчете параметров уравнения тренда на ЭВМ необходимость вести отсчет от середины ряда динамики отпадает. Например, для получения уравнения тренда в Microsoft Office Excel необходимо построить его график с помощью «Мастера диаграмм», после чего вызвать контекстное меню, нажав на правую кнопку мыши на построенном графике, и выбрать пункт «Добавить линию тренда», в появившемся окне выбрать подходящую математическую функцию и установить галочку «показывать уравнение на диаграмме»

[32] Понятие «уровень значимости» описано ранее на стр. 29

[33] Выравнивание по параболе рассмотрено в методических указаниях к теме на другом примере

[34] Используется при малом количестве уровней (n<30), в противном случае (n>30) вместо используют коэффициент доверия t нормального закона распределения (Приложение 1)

[35] Попробуйте проделать данное задание самостоятельно (в случае затруднений обратитесь к методическим указаниям по данной теме)

[36] Выполните это задание дома самостоятельно (подсказка: продифференцировав и приравняв нулю уравнение учтите, что и )

[37] Подобрать уравнение второй гармоники ряда Фурье по данным табл. 32 самостоятельно

[38] Проделайте данное задание самостоятельно

[39] Проявление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо

[40] Термин «стохастический» происходит от греч. «stochos» – мишень. Стреляя в мишень, даже хороший стрелок редко попадает в ее центр, выстрелы ложатся в некоторой близости от него. Другими словами стохастическая связь означает приблизительный характер значений признака

[41] Термин «корреляция» ввел в статистику английский биолог и статистик Ф. Гальтон в конце XIX в., под которым понималась «как бы связь», т.е. связь в форме, отличающейся от функциональной. Еще ранее этот термин применил француз Ж.Кювье в палеонтологии, где под законом корреляции частей животных он понимал возможность восстановить по найденным в раскопках частям облик всего животного

[42] Множественная корреляция изучается в курсе эконометрики на основе применения компьютерных программ (напр., специальная надстройка к Excel, SPSS и др.), в курсе статистики изучается только парная корреляция

[43] При измерении тесноты связи между рядами динамики это равнозначно отсутствию автокорреляции между уровнями ряда, т.е. прежде чем оценивать тесноту связи между рядами динамики, необходимо проверить каждый ряд на автокорреляцию – см. методические указания

[44] Проделать это самостоятельно

[45] Термин «регрессия» ввел в статистику Ф. Гальтон, который изучив большое число семей, установил, что в группе семей высокорослыми отцами сыновья в среднем ниже ростом, чем их отцы, а в группе семей с низкорослыми отцами сыновья в среднем выше отцов, т.е. отклонение роста от среднего в следующем поколении уменьшается – регрессирует

[46] Параметры a₀ и a₁ можно получить не только методом подстановки как приводится далее, но и методом определителей 2-го порядка (проделать данное задание самостоятельно)

[47] Сумма эмпирических (2864,09) и выравненных по прямой линии (2864,115) значений должна совпадать, но в нашем случае этого не происходит из-за округлений расчетов до 3-х знаков после запятой

[48] В числителе – сумма последнего столбца, а в знаменателе – сумма предпоследнего столбца таблицы 45

[49] Коэффициент автокорреляции можно рассчитывать либо между соседними уровнями, либо между уровнями, сдвинутыми на другое число единиц времени (временной лаг) m; приведенные формулы с временным лагом m=1 (между соседними уровнями) являются самыми распространенными

[50] Формула (156) является тождественной формуле (155)

[51] См. тему 5 «Ряды динамики», метод аналитического выравнивания

[52] Остаточные величины обычно обозначают ε_t, но для того, чтобы различать их для разных рядов динамики x и y, приняты обозначения d_x и d_y

[53] По значению коэффициент контингенции всегда меньше коэффициента ассоциации

[54] Такая очередность изменения факторов (то есть 1-ый – экстенсивный, а 2-ой – интенсивный) применяется по умолчанию тогда, когда ее затруднительно точно установить

[55] В случае построения многофакторных мультипликативных индексных моделей бывает сложно точно определить очередность влияния факторов на результативный показатель, поэтому можно рекомендовать ставить на 1-ое место индекс того фактора, который сильнее всего изменился, на 2-ое место – индекс того фактора, который изменился слабее первого, но сильнее остальных и так далее в порядке убывания изменений индексов

[56] Самостоятельно догадайтесь и придумайте пример, когда эффект Гершенкрона выполняться не будет (подсказка – «эффект картошки»)

[57] Если зафиксировать веса на уровне базисного периода f₀, то получим менее распространенную формулу индекса фиксированного состава: или .

[58] При фиксировании индексируемой величины на уровне отчетного периода x₀ получается менее распространенная формула индекса структурных сдвигов: или .

[59] В противном случае применяются формулы, приведенные в сносках к этим формулам. Для определения очередности влияния факторов рассчитываются и те, и другие формулы, а затем рассчитывается их средняя геометрическая величина (индексы Фишера). Сравнивая значения этих индексов Фишера, решается вопрос об очередности влияния факторов: какой из индексов показывает большее изменение, тот фактор и считают 1-ым.

[60] Выбор этой формулы вызван тем, что изменение структуры – это 1-ый фактор, и изменение самих цен – 2-ой (доказать это самостоятельно, воспользовавшись предыдущей сноской)

[61] В названии использованы начальные буквы фамилий трех статистиков, предложивших этот индекс: венгров Элтетэ и Кэвеша и поляка Шульца