Расчет прогнозируемых значений

В ряде случаев ставится задача получения численных значений аппроксимирующей функции для новых значений x_i в интервале прогнозирования. Эта задача решается с помощью маркера автозаполнения (квадратик в нижнем правом углу селектора таблицы) или посредством встроенных функций.

Прогнозирование с помощью маркера производится в следующей последовательности. Выделяются ячейки B3:B8 (с известными значениями y). Затем, с помощью маркера производится протягивание данных вниз по месяцам 7, 8, 9. Полученные в ячейках B9:B11 данные, служат для прогноза реализации продукции в ближайшие три месяца.

Прогнозирование также можно выполнить с помощью контекстного меню. Выделяются исходные данные (ячейки B3:B8). Затем производится заполнение с помощью маркера, но при нажатой правой кнопке мыши. В открывшемся меню следует выбрать или "Линейное приближение", или "Экспоненциальное приближение".

Прогнозирование можно выполнить и с помощью встроенных функций. Воспользуемся функцией ЛИНЕЙН (известные_значения_у, известные_значения_х, конст, статистика). В нашем случае известные_значения_у находятся в диа­пазоне В3:В8, а известные_значения_х – в диапазоне А3:А8. Два последних аргумента логические. Если конст – ИСТИНА или опущено, то свободный член b в регрессионном уравнении

y = mx + b

может быть любым, а если конст – ЛОЖЬ, то b принудительно полагается равным нулю. Если последний аргу­мент статистика – ЛОЖЬ или опущен, то вычисляются только коэффициенты т и b,а если ИСТИНА, то выдаются дополни­тельные статистические характеристики. Вместо слов ИСТИНА и ЛОЖЬ в функции можно вводить аргументы 1 и 0, что намного удобнее.

Так как функция возвращает сразу несколько значений, формулу с этой функцией надо вводить как табличную. Если нужно вывести полную статистику, то надо выделить блок ячеек из шести строк и двух столбцов. Выделим блок F3:G7, щелкнем по кнопке , в Мастере функций выберем в ка­тегории "Статистические" функцию ЛИНЕЙН. Первым аргу­ментом укажем блок В3:В8, вторым аргументом – блок А3:А8, в третьем и четвертом поле ввода проставим 1. Не щелкаем по кнопке "ОК", а нажимаем Ctrl+Shift+Enter (находясь в диалого­вом окне)! Получим следующую таблицу (рис. 2.85).

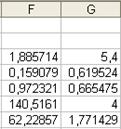
Рис. 2.85. Расчет линейной регрессии с помощью функции ЛИНЕЙН

В ячейку F3 записан коэффициент m, в G3 – коэффициент b. Под этими коэффициентами записаны стандартные отклоне­ния (т.е. среднеквадратичные отклонения, или корни квадрат­ные из дисперсий) для этих коэффициентов.

В ячейку F5 записан так называемый коэффициент детерми­нации R². Этот коэффициент лежит на отрезке [0; 1]. Считается, что чем ближе этот коэффициент к 1, тем лучше регрессионное уравнение описывает зависимость. Ниже мы убедимся, что к такой интерпретации надо относиться с осторожностью.

В ячейке G5 находится стандартная ошибка для оценки у. В ячейку F6 записано значение F-статистики, а в G6 – количест­во степеней свободы. Число степеней свободы нужно для расче­та критических значений F-статистики (этого вопроса мы ка­саться не будем).

В последней строке таблицы записаны регрессионная сумма квадратов (62,22857) и остаточная сумма квадратов (1,771429). Последнее число это сумма квадратов разностей e_i=y_i – f(x_i).

Можно и не вычислять коэффициенты регрессионного уравнения (если не требуется знать значения F-статистики), а воспользоваться одной из двух статистических функций ПРЕДСКАЗ и ТЕНДЕНЦИЯ, которые возвращают значения для новых значений x_i с применением линейной аппроксимации по методам линейного приближения (ПРЕДСКАЗ) и наименьших квадратов (ТЕНДЕНЦИЯ). Порядок применения этих функций аналогичен порядку применения функции ЛИНЕЙН.

Задания по построению уравнений регрессии

По наблюдаемым значениям величин х и у (х – не­деля, y – объем реализации) найти математическую модель, наи­лучшим образом описывающую изменение объемов реализации некоторого вида товара за последние несколько недель:

1.	x
	y

2.

x

y

3.

x

y

4.	x
	y

5.	x
	y

6.	x
	y

7.	x
	y

8.	x
	y

9.

x

y

10.	x
	y

11.	x
	y

12.	x
	y