Виды аппроксимирующих функций и их описание

С помощью MS Excel можно также проводить автоматический анализ тренда на основе диаграмм. Для того чтобы правильно выбрать линию тренда на диаграмме, следует хорошо разбирать­ся в теоретических основах прогнозирования. Линию тренда можно добавить к ряду данных в том случае, если они представ­ляют собой диаграмму с областями, график, гистограмму, линей­чатую или точечную диаграмму.

В MS Excel предлагается выбрать одну из пяти типов аппрокси­мирующих линий или вычисление линии, показывающей сколь­зящее среднее. Скользящее среднее сглаживает флуктуации ряда данных, помещая отдельную точку данных на линии тренда на основании среднего для указанного числа первичных точек данных. Указанный выбор осуществляется на вкладке Тип диалогового окна Линия тренда(рис. 2.80), которое открывается по команде Диаграмма/Добавить линию тренда.Описание типов выби­раемых линий приведено в табл. 2.26.

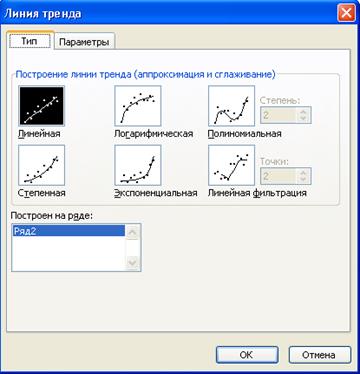
Рис. 2.80.Окно Линия тренда, вкладка Тип

Таблица 2.26.Описание типов линий тренда

Тип	Описание
1. Линейная	Аппроксимирующая прямая: у = ax + b , где а – тангенс угла наклона, b – точка пере­сечения прямой с осью Y
2. Логарифмическая	Логарифмическая аппроксимация: y=aln(x) + b , где а и b – константы, ln – натуральный лога­рифм
3.Полиномиальная	Полиномиальная аппроксимация: у = ax6 + а2х5 + а3х4 + а4х3+ a5x2 + а6х + b, где аi, ,и b – константы. Максимальная степень полинома – 6
4. Степенная	Степенная аппроксимация: y = axb ,где а и b – константы
5. Экспоненциальная	Экспоненциальная аппроксимация: y = aebx, где а и b – константы, е – основание нату­рального логарифма
6. Линейная фильтрация	Скользящее среднее. Каждая точка данных на линии тренда строится на основании среднего указанного числа точек данных (периодов). Чем больше число периодов, используемых для вы­числения скользящего среднего, тем более гладкой, но менее точной становится линия тренда

Необходимо учитывать также и настройки, которые можно сделать на вкладке Параметрыдиалогового окна Линия тренда (рис. 2.81):

· в области Название аппроксимирующей (сглаженной) кривой– задается название аппроксимирующей кривой;

· в области Прогноз– задается прогнозирование данных (впе­ред) или определяется история данных (назад) с помощью ли­нии тренда;

· флажок Пересечение кривой с осью Y в точке– устанавли­вается лишь в том случае, если эта точка известна;

· флажок Показывать уравнение на диаграмме–обеспечи­вает размещение на диаграмме уравнения аппроксимирующей функции с числовыми коэффициентами.

· флажок Поместить на диаграмму величину достоверности аппроксимации (R^2)–обеспечивает размещение на диаграмме квадрата коэффициента корреляции.

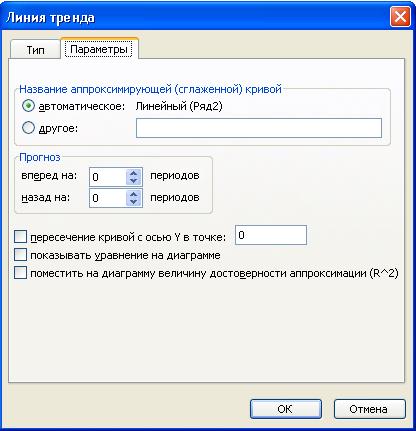
Рис. 2.81.Окно Линия тренда, вкладка Параметры

Примечание. Величина достоверности аппроксимации является одним из важ­нейших показателей, которые следует разместить на диаграмме. По этой величине (т. е. квадрату коэффициента корреляции) мож­но судить о правомерности использования того или иного уравне­ния регрессии. Если коэффициент лежит в диапазоне 0,9–1, то данную зависи­мость можно использовать для предсказания результата. Чем ближе к 1 коэффициент корреляции, тем более достоверна ис­пользуемая модель. Если коэффициент корреляции приближает­ся k-1, то это говорит об обратной зависимости между наблю­даемыми величинами.

Для добавления линии тренда к ряду данных диаграммы выполните следующие шаги:

1. Выделите диаграмму, для данных которой нужно добавить линию тренда.

2. Выберите команду Диаграмма/Добавить линию тренда.

3. В окне Линия тренда(см. рис. 2.80) отметьте ряд, для которо­го строится линия тренда, и выберите тип аппроксимации (вкладка Тип),а также установите параметры линии тренда (вкладка Параметры), нажмите кнопку ОК.

Примечание.Следует помнить, что при добавлении линии тренда к ряду дан­ных она с этим рядом связывается. Любые изменения значений точек ряда данных автоматически отражаются на линии тренда — происходит ее пересчет. Если ряд данных удаляется, то удаляет­ся также и линия тренда. Если тип диаграммы для ряда данных заменяется другим, кото­рый не входит в перечень допустимых (диаграмма с областями, график, гистограмма, линейчатая или точечная диаграмма), то ли­ния тренда удаляется.

Задание 15.1. Построение линий тренда и поиск подходящего

Уравнения регрессии

Имеются две наблюдаемые величины х и у, например, объемы потребления некоторого вида продукции за последние несколько месяцев (х – месяц, y – объем потребления). Необходимо найти математическую модель, наилучшим образом описывающую наблюдаемые значения.

Алгоритм поиска подхо­дящего уравнения регрессии.

1. Разместите на рабочем листе в виде таблицы наблюдаемые величины: х, у (как это сделано на рис. 2.82).

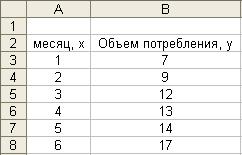
Рис. 2.82. Исходные данные

2. Постройте график функции у=f(x)по значениям этих величин (рис. 2.83).

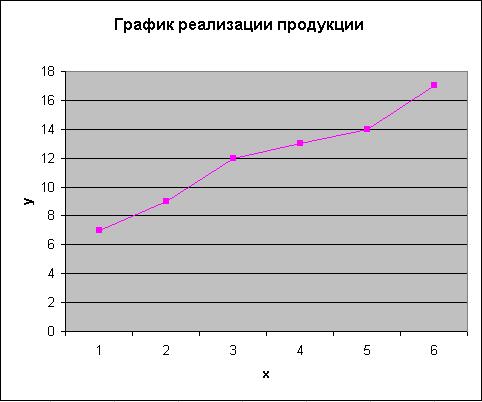
Рис. 2.83. График функции y=f(x)

3. Постройте несколько линий тренда для исходных значений. С этой целью выделите диаграмму с графиком и выполните коман­ду меню Диаграмма/Добавить линию тренда,либо воспользуйтесь соответствующей командой контекстного меню.

4. В окне Линия тренда отметьте ряд, для которого строится линия тренда, и откройте вкладку Тип. Для каждого типа аппроксимирующей кривой (линейной, степенной, логарифмической и полиномиальной) выбрав вкладку Параметры установите флажки в поляПоказывать уравнение на диаграммеиПоместить на диаграмму величину достоверности аппроксимации (R^2).После установки параметров линии тренда нажмите кнопкуОК.Построенные линии тренда приведены на рис. 2.84.

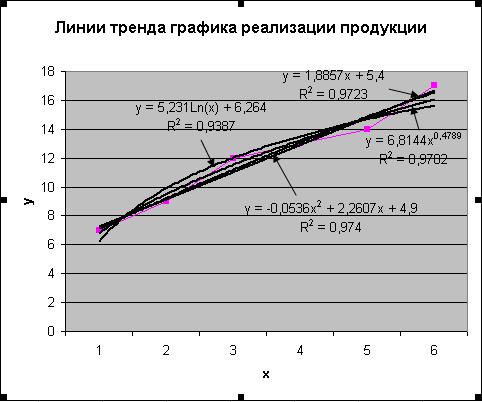
Рис. 2.84. Линии тренда для исходного графика y=f(x)

5. Задайте интервал прогнозирования и определите историю данных (т. е. продлить линии тренда за исходную область данных). Интервал прогнозирования устанавливается с помощью кнопок Вперед на: и Назад на:(с шагом в полпериода) в поле Прогноз диалогового окна Линия тренда либо с клавиатуры (с любой дробностью).

6. Делается вывод о выборе того или иного типа аппроксимации и выписать аппроксимирующее уравнение линии, выделив ко­эффициенты. Исходя из результатов расчета, для описания данных наблюдаемых величин наиболее достоверной представляется линейная модель

y = 1,8857x + 5,4; R² = 0,9723.

Замечание.Часто для аппроксимации произвольной выборки и разброса дан­ных подходит полиномиальное уравнение той или иной степени. Однако при прогнозировании уравнениями таких линий следует иметь в виду, что возможны большие ошибки в прогнозах и исто­рии данных. В таких случаях, если находится другая функция с близким коэффициентом корреляции, следует учесть ее уравнение регрессии.