Алгоритмы циклической структуры

Цикломназывают повторение одних и тех же действий (шагов).

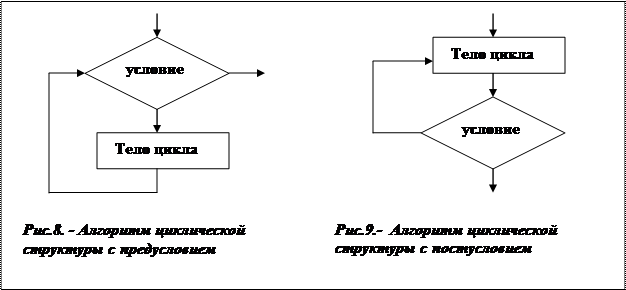
Последовательность действий, которые повторяются в цикле, называют телом цикла. Существует несколько типов алгоритмов циклической структуры. На рис. 8 изображен цикл с предусловием, а на рис. 9 – цикл с постусловием, которые называют условными циклическими алгоритмами. Нетрудно заметить, что эти циклы взаимозаменяемы и обладают некоторыми отличиями. В цикле с предусловием условие проверяется до тела цикла, в цикле с постусловием – после тела цикла. В цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с предусловием тело цикла может не выполниться ни разу. В цикле с предусловием проверяется условие продолжения цикла, в цикле с постусловием – условие выхода из цикла.

При написании условных циклических алгоритмов следует помнить следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла. Кроме того, существует так называемый безусловный циклический алгоритм, который удобно использовать, если известно, сколько раз необходимо выполнить тело цикла. Выполнение безусловного циклического алгоритма начинается с присвоения переменной iстартового значения i_n. Затем следует проверка, не превосходит ли переменная iконечное значение i_к. Если превосходит, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. В противном случае выполняется тело цикла, и переменная iменяет свое значение в соответствии с указанным шагом d_i. Далее, снова производится проверка значения переменной iи алгоритм повторяется. Понятно, что безусловный циклический алгоритм можно заменить любым условным.

Отметим, что переменную iназывают параметром цикла, так как это переменная, которая изменяется внутри цикла по определенному закону и влияет на его окончание. Рассмотрим использование алгоритмов циклической структуры на конкретных примерах.

Пример 1. Найти наибольший общий делитель (НОД) двух натуральных чисел (А, В).

Входные данные: А и В. Выходные данные: А – НОД.

Для решения поставленной задачи воспользуемся алгоритмом Евклида: будем уменьшать каждый раз большее из чисел на величину меньшего до тех пор, пока оба значения не станут равными, так, как показано в блок-схеме на рис. 11.

Пройдем алгоритм Евклида в соответствии с блок-схемой для поиска НОД чисел А=25 и В=15.

Исходные данные

Первый шаг	Второй шаг	Третий шаг	НОД(А,В)=5
А=25	А=10	А=10	А=5
В=15	В=15	В=5	В=5

В блок–схеме для решения поставленной задачи используется цикл с предусловием, то есть тело цикла повторяется до тех пор, пока А не равно В.

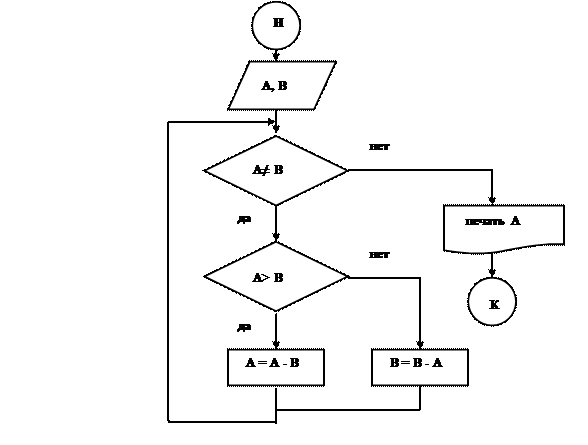
Рис.11. - Блок-схема вычисления наибольшего общего делителя двух чисел

Пример 2. Вводится последовательность чисел, 0 – конец последовательности. Определить, содержит ли последовательность хотя бы два равных соседних числа.

Например, в последовательности 7, 12, 25, 25, 6, 9, 9, 14, 0 – две пары равных соседних чисел: 25 и 9.

Входные данные: X₀ – текущий член последовательности, X₁ – следующий член последовательности.

Выходные данные:сообщение о наличии в последовательности двух равных соседних элементов. Усилим задачу подсчетом количества таких совпадающих пар.

Вспомогательные переменные: Fl – логическая переменная, сохраняет значение «истина», если в последовательности есть равные рядом стоящие члены и «ложь» - иначе. К –количество совпадающих пар. Первоначальное значение К = 0.Если находим совпадающую пару, количество совпадающих парКувеличивается на единицу: К = К + 1.

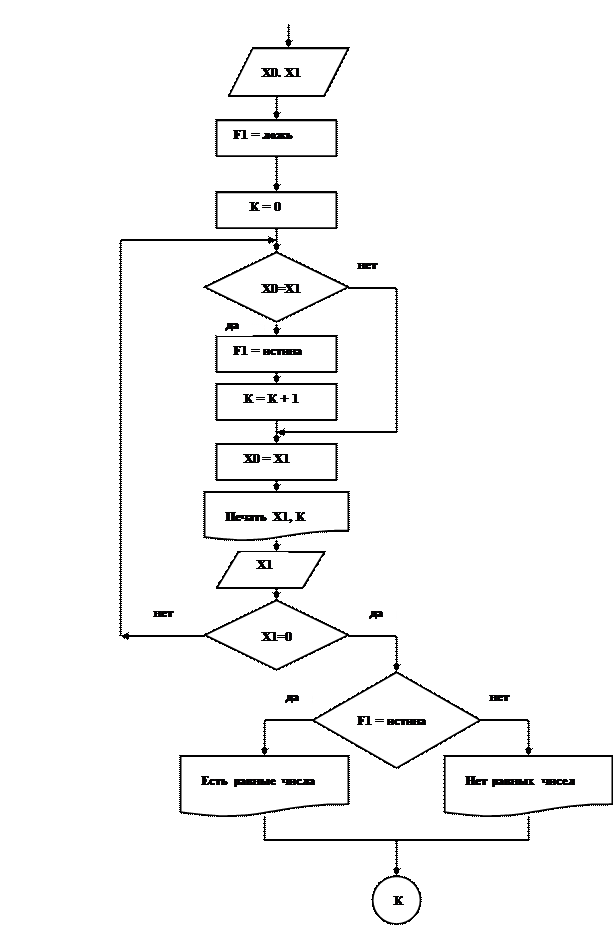
Рис.12. - Блок-схема нахождения совпадающих элементов

Блок–схема решения задачи приведена на рис. 12. Применение здесь цикла с постусловием обосновано тем, что необходимо вначале сравнить два элемента последовательности, а затем принять решение об окончании цикла. Обратите внимание на то, что выражение «Х0 = Х1»в логическом блоке (ромб) имеет смысл сравнения, т.е. выясняется, совпадают ли эти значения, а в блоке присваивания (прямоугольник) эта же запись имеет смысл присваивания, т.е. в ячейку с именем Х0записывается числоХ1.

В приведенных примерах условие задачи таково, что неизвестно, сколько раз повторится тело цикла. Такие циклы называют циклами с неизвестным числом повторений (вообще говоря, неизвестно, закончится ли цикл вообще). Цикл, количество повторений которого известно заранее или его можно определить по исходным данным, называют циклом с известным числом повторений.

Рассмотрим несколько примеров с использованием таких циклов.

Пример 3. Составить таблицу значений функции y = e^sin(x)cos(x)на отрезке [0;2]с шагом h= 0.1. Первый способ.

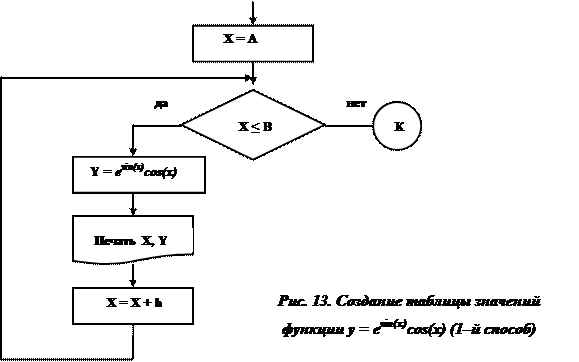Входные данные:начальное значение аргумента A = 0, конечное значение аргумента B = 2, шаг изменения аргумента – 0.1.

Выходные данные:множество значений аргумента X и соответствующее им множество значений функции Y.

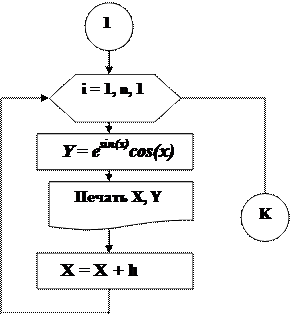
Пример 4. Составить таблицу значений функции y = e^sin(x)cos(x)на отрезке [0;2]с шагом h= 0.1. Второй способ.

Входные данные:начальное значение аргумента A = 0, конечное значение аргумента B = 2, шаг изменения аргумента – 0.1.

Выходные данные:множество значений аргумента X и соответствующее им множество значений функции Y.

Решение. Поскольку известно, как изменяется параметр цикла X и каковы его начальное и конечное значения, можно, предварительно определив количество повторений тела цикла n, воспользоваться безусловным циклическим оператором. Итак, если параметр цикла Х принимает значения в диапазоне от Х_n до Х_k, изменяясь с шагом h_х, то количество повторений тела цикла можно определить по формуле: 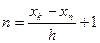, округлив результат деления до целого числа.

		Рис. 14. Создание таблицы значений функции y = esin(x)cos(x) (2–й способ)

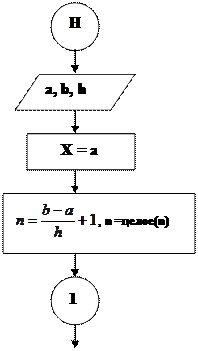Выполнение алгоритма: здесь i –переменная типа пересчета,которая принимает значения 1, 2, …..( с шагом h=1) ; для каждого значения iдля текущего значенияХвычисляется соответствующее значение функции Y, до тех пор, пока переменная пересчета iне примет значение, равное n.

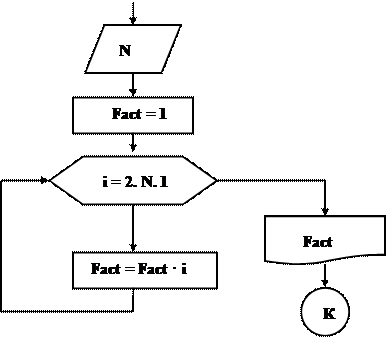
Пример 5. Вычислить факториал числаN (N!=1·2·3· …N).

Входные данные: N– целое число, факториал которого необходимо вычислить.

Выходные данные: Fact–значение факториала числа N, произведение чисел от 1 до N, целое число.

Промежуточные данные: i– целочисленная переменная, принимающая значения от 2 до N с шагом 1, параметр цикла. Блок-схема приведена на рис.15.

	Рис. 15. - Вычисление факториалачисла N

Итак, вводится число N. Переменной Fact,предназначенной для хранения значения произведения последовательности чисел, присваивается начальное значение, равное единице. Затем организуется цикл, параметром которого выступает переменная i. Если значение параметра цикла меньше или равно N, то выполняется оператор тела цикла, в котором из участка памяти с именем Factсчитывается предыдущее значение произведения, умножается на текущее значение параметра цикла, а результат снова помещается в участок памяти с именем Fact. Когда параметр i становится больше N,цикл заканчивается, и на печать выводится значение переменой Fact,которая была вычислена в теле цикла.

Пример 6.Вычислить aⁿ (n>0).

Входные данные: a– вещественное число, которое необходимо возвести в целую положительную степень n.

Выходные данные: p (вещественное число) –результат возведения вещественного числа a в целую положительную степень n.

Промежуточные данные: i– целочисленная переменная, принимающая значения от 1 до nс шагом 1, параметр цикла. Блок-схема приведена на рис.16.

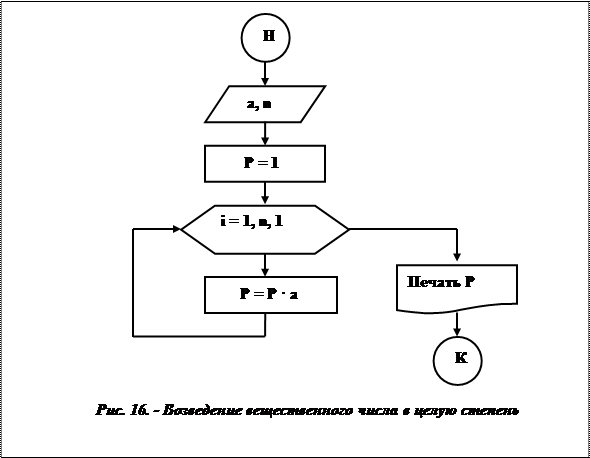Итак, известно, что для того, чтобы получить целую степень n числа a, нужно умножить его само на себя n раз. Результат этого умножения будет храниться в участке памяти с именем Р. При выполнении очередного цикла из этого участка предыдущее значение будет считываться, умножаться на основание степени a и снова записываться в участок памяти Р. Цикл выполняется nраз.

В следующей таблице отображен протокол выполнения алгоритма при возведении числа 2

в пятую степень: a=2, n=5. Подобные таблицы, заполненные вручную, используются для тестирования – проверки всех этапов работы программы.

i
P