Оценка погрешности измерений. Доверительные интервалы

Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов.

Симметричный интервал в границами Δх(Р) называется доверительным интервалом случайной погрешности с доверительной вероятностью Р, если площадь кривой распределения между абсциссами –Δх и +Δхсоставляет Р-ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах).

Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р×100% всех возможных значений случайной погрешности.

Доверительный интервал для нормального распределения находится по формуле:

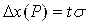
где коэффициент t зависит от доверительной вероятности Р.

Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью:

1s (Р=0,68);

2s (Р= 0,95);

3s (Р= 0,997);

4s (Р=0,999).

Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными.

Так, в анализах данных продаж недвижимости наиболее часто принимается доверительная вероятность 0,95, т.е. используя правило двух сигм 2s (Р= 0,95). Уровень значимости составляет 5% (1-0,95). Это означает, что точность анализа данных составляет 95%.

Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверительные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф.

При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле:

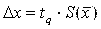
где tq– коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q-процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q= 1 – P; 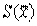– оценка среднего квадратического отклонения среднего арифметического.

Доверительный интервал для погрешности Dх(Р) позволяет построить доверительный интервал для истинного (действительного) значения измеряемой величины, оценкой которой является среднее арифметическое .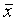

Истинное значение измеряемой величины находится с доверительной вероятностью Р внутри интервала:

.

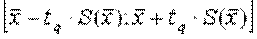Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами. Недостатком доверительных интервалов при оценке случайных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погрешностей, т.к. доверительный интервал суммы не равен сумме доверительных интервалов. Суммируются дисперсии независимых случайных величин: Då = åDi.

То есть, для возможности суммирования составляющие случайной погрешности должны быть представлены своими средними квадратическими отклонениями (СКО), а не предельными или доверительными погрешностями.

Наличие данных о погрешности в определении средних цен объектов недвижимости позволяет при сравнении двух выборок (например, по двум различным районам или за два месяца) использовать следующее правило: выборки считаются различающимися незначимо, если разность их средних меньше суммы половины погрешностей.

2) Аппроксимация. Динамические ряды. Статистическое прогнозирование.

Аппроксимация (метод приближения)- приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач. В экономике целью аппроксимации часто является укрупнение характеристик моделируемых экономических объектов.

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

Аппроксимация линейной функцией

Любая линейная функция может быть записана уравнением

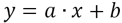
Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой. С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:

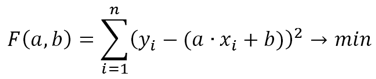
Линейная аппроксимация - линия регрессии - представлена на графике (рис.1). Черными кружками отмечены выборочные значения. Размер кружков соответствует их частотам.

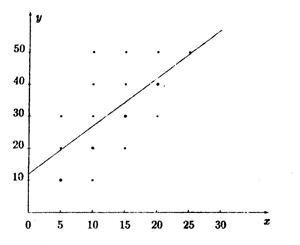
Рис. 1 Аппроксимация линейная

Аппроксимация интегральная (криволинейная корреляция)

Если линейная аппроксимация статистической зависимости между двумя величинами не отражает характер зависимости, используют модель криволинейной корреляции. Одной из распространенных является параболическая корреляция второго порядка, при которой уравнение регрессии Y на X имеет вид:

.

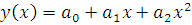На практике выборка совместного распределения случайных величин X и Y возникает как последовательность пар 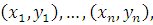перечисленных в порядке произведенных наблюдений, среди них могут быть и одинаковые. Для нахождения коэффициентов регрессии можно, но не обязательно группировать данные в корреляционную таблицу. Например, данные по увеличению стоимости и полученной прибылью от продаж для N – го количества выбранных объектов можно свести в таблицу.

Увеличение стоимости Х
Прибыль Y

Заметим, что устанавливаемое увеличение стоимости по смыслу является величиной неслучайной, принятой на основании анализа рынка и статистических обработок данных. Прибыль, определяемая количеством проданных объектов, напротив, величина случайная, среднее значение которой зависит от принятого увеличения стоимости.

Уравнение регрессии Y на X необходимо найти в виде:

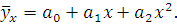
Решение уравнения даст возможность построить график.

На графике представлены значения полученных прибылей при различных увеличениях стоимости объектов и полученная по ним параболическая линия регрессии. Таким образом, на рис.2 представлен вид графика криволинейной корреляции.

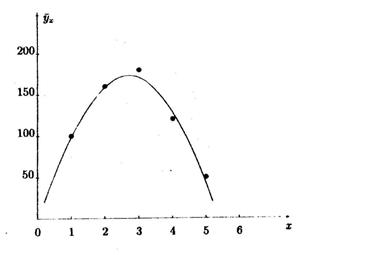
Рис.2. Аппроксимация интегральная

Динамический ряд — это ряд однородных статистических величин, показывающих изменение явления во времени. Динамический ряд может быть представлен абсолютными числами (изменение числа проданных объектов недвижимости за определенный период времени), средними величинами (средняя цена единицы измерения, например, квадратного метра жилья, в разрезе районов города, реализованных за год) и относительными показателями (изменение стоимости за несколько месяцев, обычно не более года). Числа, из которых состоит динамический ряд, называются уровнями ряда. Анализ динамического (временного) ряда сводится к вычислению следующих показателей: абсолютного прироста (или снижения); темпа роста (или снижения); темпа прироста; значения 1% прироста.

Абсолютный приростпредставляет собой разность между последующим и предыдущим уровнем.

Темп роста — это отношение последующего уровня к предыдущему, умноженное на 100%.

Темп приростаявляется отношением абсолютного прироста (снижения) к предыдущему уровню, умноженным на 100%.

Значение 1% прироста определяется отношением абсолютного прироста к темпу прироста.

Условия правильного построения динамических рядов

Основным условием правильного построения динамического ряда - это обеспечение сопоставимости уровней ряда (числовых значений изучаемого явления).

Сопоставимость уровней (показателей) ряда обеспечивается путем строгого соблюдения целого ряда правил построения динамического ряда:

· все показатели динамического ряда должны быть выражены в одних и тех же единицах измерения.

· все показатели динамического ряда рассчитываются по единой методике, одним и тем же способом.

· все показатели динамического ряда должны быть одинаковы по полноте охвата изучаемой совокупности. Это означает, что все показатели динамического ряда должны относиться к равным периодам времени (или за месяц, или за квартал, или за год и т.д.), к одной и той же территории.

Для правильного построения динамического ряда необходимо обеспечить полную достоверность всех показателей ряда, их научную обоснованность, так как любая небрежность, неточность может и корне исказить исследуемую закономерность (тенденцию).

На рисунках 3,4 приведены примеры вариантов построения динамического ряда.

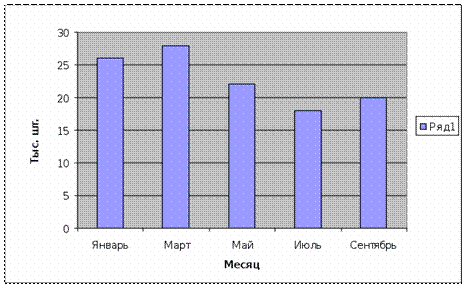
Рис.3 Динамический ряд

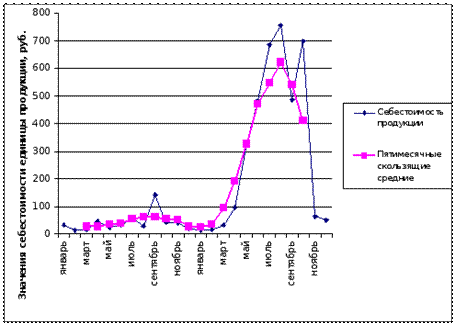
Рис.4. Динамический ряд