Методы анализа больших систем

Теория систем большей частью основывает свои практические методы на платформе математической статистики. Можно выделить три подхода к решению задач, в которых используются статистические данные [5].

Алгоритмический подход, при котором мы имеем статистические данные о некотором процессе и по причине слабой изученности процесса его основную характеристику (например, эффективность экономической системы) мы вынуждены сами строить “разумные” правила обработки данных, базируясь на своих собственных представлениях об интересующем нас показателе.

Аппроксимационный подход, когда у нас есть полное представление о связи данного показателя с имеющимися у нас данными, но неясна природа возникающих ошибок — отклонений от этих представлений.

Теоретико-вероятностный подход, когда требуется глубокое проникновение в суть процесса для выяснения связи показателя со статистическими данными.

В настоящее время все эти подходы достаточно строго обоснованы научно и “снабжены” апробированными методами практических действий.

Но существуют ситуации, когда нас интересует не один, а несколько показателей процесса и, кроме того, мы подозреваем наличие нескольких, влияющих на процесс, воздействий — факторов, которые являются не наблюдаемыми, скрытыми или латентными.

Наиболее интересным и полезным в плане понимания сущности факторного анализа — метода решения задач в этих ситуациях, является пример использования наблюдений при эксперименте, который ведет природа. Ни о каком планировании здесь не может идти речь — нам приходится довольствоваться пассивным экспериментом.

Удивительно, но и в этих “тяжелых” условиях теория систем предлагает методы выявления таких факторов, отсеивания слабо проявляющих себя, оценки значимости полученных зависимостей показателей работы системы от этих факторов.

Пусть мы провели по n наблюдений за каждым из kизмеряемых показателей эффективности некоторой системы и данные этих наблюдений представили в виде матрицы (таблица 1).

Таблица 1- Матрица исходных данных E[n·k]

E 11	E12	…	E1i	…	E1k
E 21	E22	…	E2i	…	E2k
…	…	…	…	…	…
E j1	Ej2	…	Eji	…	Ejk
…	…	…	…	…	…
E n1	En2	…	Eni	…	Enk

Пусть мы предполагаем, что на эффективность системы влияют и другие — ненаблюдаемые, но легко интерпретируемые (объяснимые по смыслу, причине и механизму влияния) величины — факторы.

Сразу же сообразим, что чем больше n и чем меньше число факторов m(а может их и нет вообще!),тем больше надежда оценить их влияние на интересующий нас показательE.

Столь же легко понять необходимость условияm < k, объяснимогона простом примере аналогии — если мы исследуем некоторые предметы с использованием всех 5 человеческих чувств, то наивно надеяться на обнаружение более пяти “новых”, легко объяснимых, но неизмеряемых признаков у таких предметов, даже если мы “испытаем” очень большое их количество.

Вернемся к исходной матрице наблюдений E[n·k] и отметим, что перед нами, по сути дела, совокупности по n наблюдений над каждой из k случайных величин E₁, E₂, … E _k. Именно эти величины “подозреваются” в связях друг с другом — или во взаимной коррелированности.

Из рассмотренного ранее метода оценок таких связей следует, что мерой разброса случайной величины E_iслужит ее дисперсия, определяемая суммой квадратов всех зарегистрированных значений этой величины S(E_ij)² и ее средним значением (суммирование ведется по столбцу).

Если мы применим замену переменных в исходной матрице наблюдений, т.е. вместо E_{i j} будем использовать случайные величины

X_ij = ,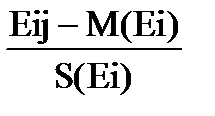

то мы преобразуем исходную матрицу в новую X[n·k](таблица 2)

Таблица 2- Матрица преобразованных данных Х[n·k]

X 11	X12	…	X1i	…	X1k
X 21	X22	…	X2i	…	X2k
…	…	…	…	…	…
X j1	Xj2	…	Xji	…	Xjk
…	…	…	…	…	…
X n1	Xn2	…	Xni	…	Xnk

Отметим, что все элементы новой матрицы X[n·k] окажутся безразмерными, нормированными величинами и, если некоторое значение X_ijсоставит, к примеру,+2, то это будет означать только одно - в строке j наблюдается отклонение от среднего по столбцу i на два среднеквадратичных отклонения (в большую сторону).

Выполнимтеперь следующие операции.

1) Просуммируем квадраты всех значений столбца 1 и разделим результат на (n - 1) — мы получим дисперсию (меру разброса) случайной величины X₁, т.е. D₁.Повторяя эту операцию, мы найдем таким же образом дисперсии всех наблюдаемых (но уже нормированных) величин.

2) Просуммируем произведения элементов соответствующих строк (от i=1 до i= n) для столбцов 1, 2 и также разделим на (n -1), то теперь мы получим коэффициент ковариации C₁₂случайных величин X₁ , X₂, который служит мерой их статистической связи.

3) Если мы повторим предыдущую процедуру для всех пар столбцов, то в результате получим еще одну, квадратную матрицу C[k·k], которую принято называть ковариационной (таблица 3).

Этаматрица имеет на главной диагонали дисперсии случайных величин X_i, а в качестве остальных элементов — ковариации этих величин (i =1…k).

Таблица 3 - Ковариационная матрица C[k·k]

D1	C12	C13	…	…	C1k
C21	D2	C23	…	…	C2k
…	…	…	…	…	…
Cj1	Cj2	…	Dj	…	Cjk
…	…	…	…	…	…
Ck1	Ck2	…	Cki	…	Dk

Если вспомнить, что связи случайных величин можно описывать не только ковариациями, но и коэффициентами корреляции, то в соответствие матрице табл.3 можно поставить матрицу парных коэффициентов корреляции или корреляционную матрицу (таблица 4), в которой на диагонали находятся 1, а недиагональными элементами являются коэффициенты парной корреляции.

Таблица 4- Корреляционная матрица R [k·k]

	R12	R13	…	…	R1k
R21		R23	…	…	R2k
…	…	…	…	…	…
Rj1	Rj2	…	Rji	…	Rjk
…	…	…	…	…	…
Rk1	Rk2	…	Rki	…

Так, если мы полагали наблюдаемые переменные E_i независящими друг от друга, то ожидалиувидеть матрицуR[k·k]диагональной, с единицамина главной диагонали и нулями в остальных местах. Если это не так, то наши догадки о наличии латентных факторов в какой-то мере получают подтверждение.

Но как убедиться в своей правоте, оценить достоверность нашей гипотезы — о наличии хотя бы одного латентного фактора, как оценить степень его влияния на основные (наблюдаемые) переменные? А если, тем более, таких факторов несколько — то как их проранжировать по степени влияния?

Ответы на такие практические вопросы призван давать факторный анализ. В его основе лежит все тот же “вездесущий” метод статистического моделирования (по образному выражению В.В. Налимова — модель вместо теории).

Дальнейший ход анализа при выяснении таких вопросов зависит от того, какой из матриц мы будем пользоваться. Если матрицей ковариаций C[k·k], то мы имеем дело с методом главных компонент, если же мы пользуемся только матрицей R[k·k],то мы используем метод факторного анализа в его “чистом” виде.

Остается разобраться в главном — что позволяют оба эти метода, в чем их различие и как ими пользоваться. Назначение обоих методов одно и то же — установить сам факт наличия латентных переменных (факторов), и если они обнаружены, то получить количественное описание их влияния на основные переменные E_i.

Компонентный анализ

Компонентный анализ является методом определения структурной зависимости между случайными переменными [5]. Идея метода заключается в замене сильно коррелированных переменных новыми переменными (главными компонентами), между которыми корреляция отсутствует. В результате его использования получается сжатое описание малого объема, несущее почти всю информацию, содержащуюся в исходных данных. Главные компоненты получаются из исходных переменных путем целенаправленного вращения, т.е. как линейные комбинации исходных переменных. Вращение производится таким образом, чтобы главные компоненты были ортогональны и имели максимальную дисперсию среди возможных линейных комбинаций исходных переменных. При этом переменные не коррелированны между собой и упорядочены по убыванию дисперсии (первая компонента имеет наибольшую дисперсию). Кроме того, общая дисперсия после преобразования остается без изменений.

Ход рассуждений при выполнении поиска главных компонент заключается в следующем. Мы предполагаем наличие некоррелированных переменных Z_j ( j=1…k), каждая из которых представляется нам комбинацией основных переменных (суммирование по i =1…k):

Z_j = S A_{j i} ·X _i

и, кроме того, обладает дисперсией, такой что

D(Z₁) ³ D(Z₂) ³ … ³ D(Z_k).

Поиск коэффициентов A_{j i}(их называют весом j-й компоненты в содержании i-й переменной) сводится к решению матричных уравнений и не представляет особой сложности при использовании компьютерных программ. Но суть метода весьма интересна и на ней стоит задержаться.

Как известно из векторной алгебры, диагональная матрица [2·2] может рассматриваться как описание 2-х точек (точнее — вектора) в двумерном пространстве, а такая же матрица размером [k·k]—как описание k точек k-мерного пространства.

Так вот, замена реальных, хотя и нормированных переменных X_i на точно такое же количество переменных Z _jозначает не что иное, как поворот kосей многомерного пространства.

“Перебирая” поочередно оси, мы находим вначале ту из них, где дисперсия вдоль оси наибольшая. Затемделаем пересчет дисперсий для оставшихсяk-1осей и снова находим “ось-чемпион” по дисперсии и т.д.

Образно говоря, мы заглядываем в куб (3-х мерное пространство) по очереди по трем осям и вначале ищем то направление, где видим наибольший “туман” (наибольшая дисперсия говорит о наибольшем влиянии чего-то постороннего); затем “усредняем” картинку по оставшимся двум осям и сравниваем разброс данных по каждой из них — находим “середнячка” и “аутсайдера”. Теперь остается решить систему уравнений — в нашем примере для 9 переменных, чтобы отыскать матрицу коэффициентов (весов) A[k·k].

Если коэффициенты A_{j i} найдены, то можно вернуться к основным переменным, поскольку доказано, что они однозначно выражаются в виде (суммирование по j=1…k)

X _i = S A_ji·Z _j .

Отыскание матрицы весов A[k·k]требует использования ковариационной матрицы и корреляционной матрицы.

Таким образом, метод главных компонент отличается прежде все тем, что дает всегда единственное решение задачи. Правда, трактовка этого решения своеобразна.

1) Мы решаем задачу о наличии ровно стольких факторов, сколько у нас наблюдаемых переменных, т.е. вопрос о нашем согласии на меньшее число латентных факторов невозможно поставить;

2) В результате решения, теоретически всегда единственного, а практически связанного с громадными вычислительными трудностями при разных физических размерностях основных величин, мы получим ответ примерно такого вида — фактор такой-то (например, привлекательность продавцов при анализе дневной выручки магазинов) занимает третье место по степени влияния на основные переменные.

Этот ответ обоснован — дисперсия этого фактора оказалась третьей по крупности среди всех прочих. Больше ничего получить в этом случае нельзя. Другое дело, что этот вывод оказался нам полезным или мы его игнорируем — это наше право решать, как использовать системный подход.

Пример. Имеются данные, описывающие зависимость результирующей переменной «y» от факторных переменных x₁ – x₃ (таблица 5).

Требуется выделить главные компоненты и построить уравнение регрессии на главных компонентах.

Перед тем как проводить компонентный анализ, проводится анализ независимости исходных признаков. Проверяется значимость матрицы парных корреляций с помощью критерия Уилкса.

Выдвигается гипотеза: Н₀: 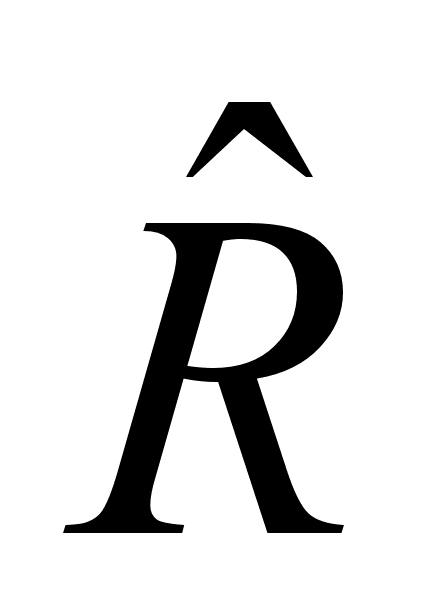незначима и альтернативная Н₁: 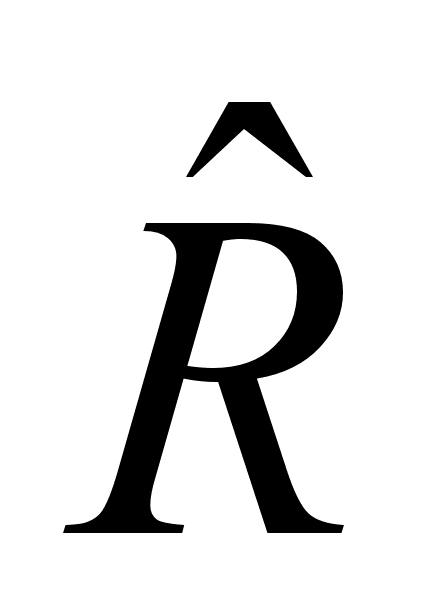значима.

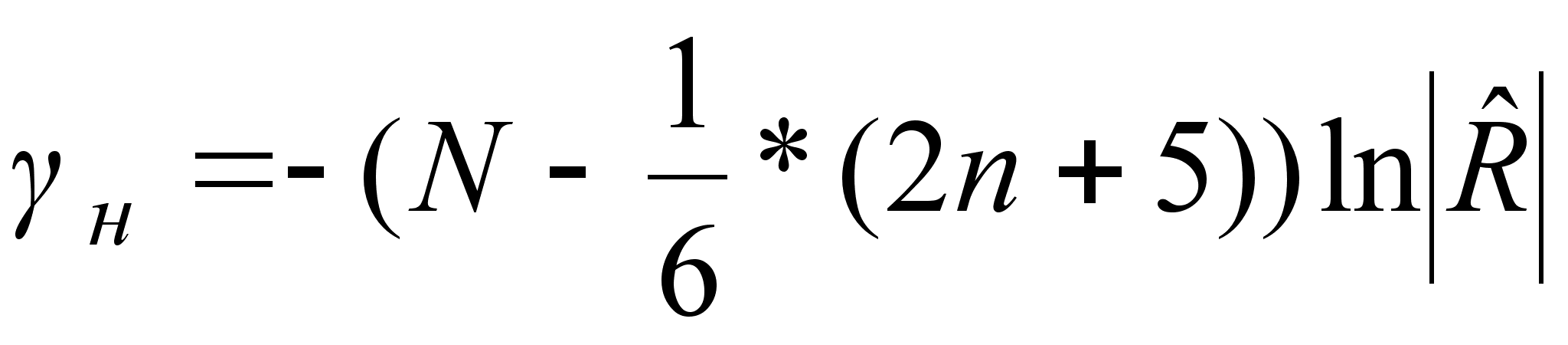
Рассчитывается статистика, которая распределена по закону 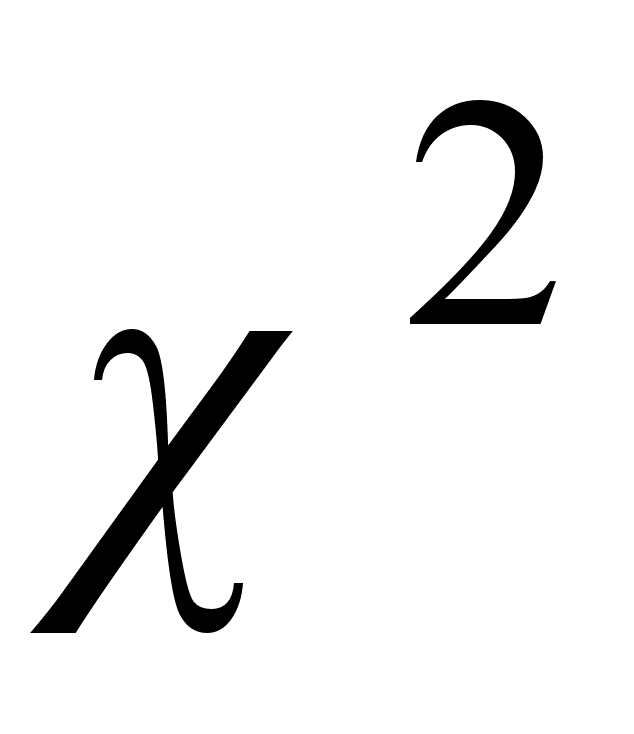с - с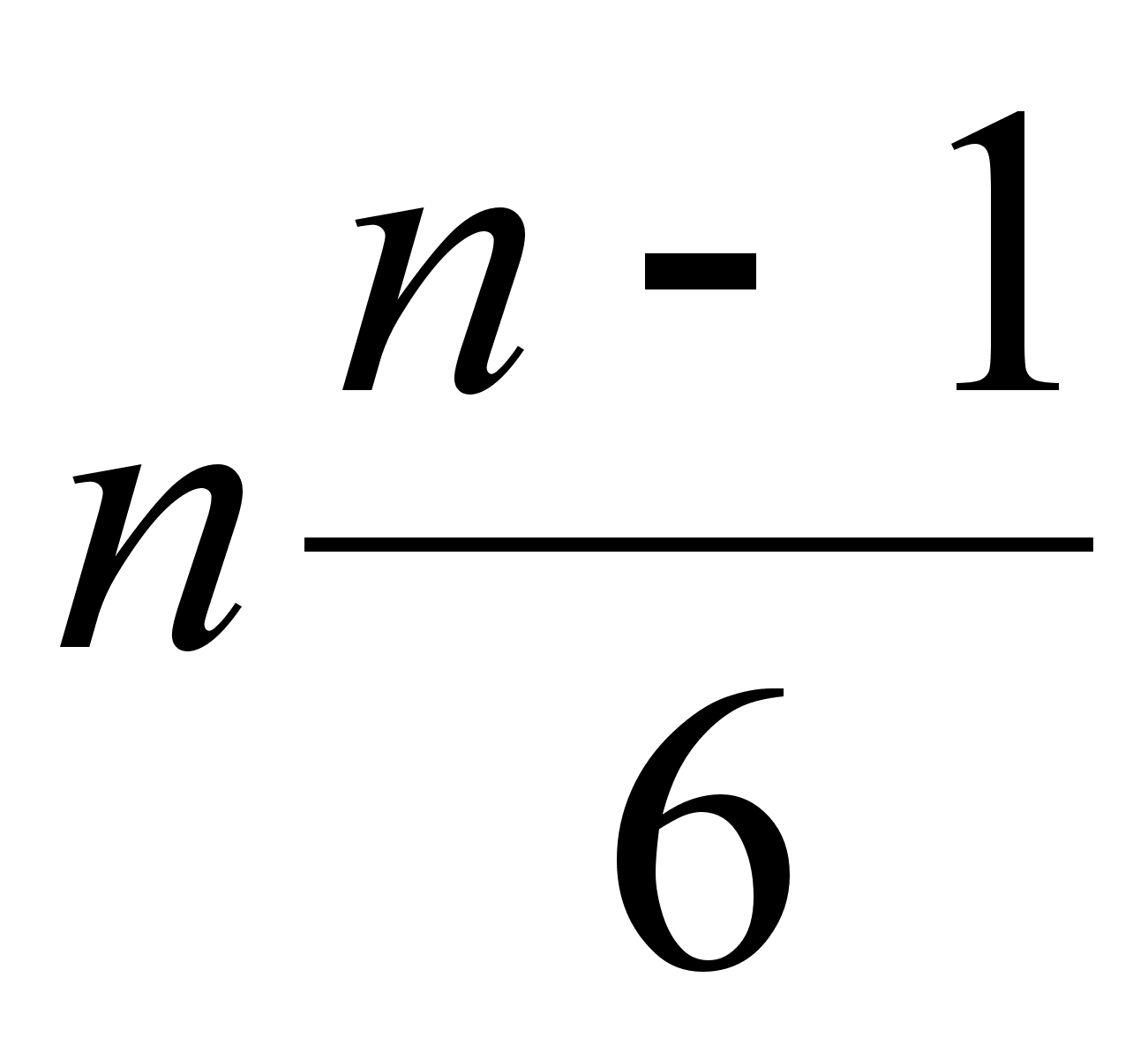тепенями свободы. Сравнивается расчетное значение с табличным значением 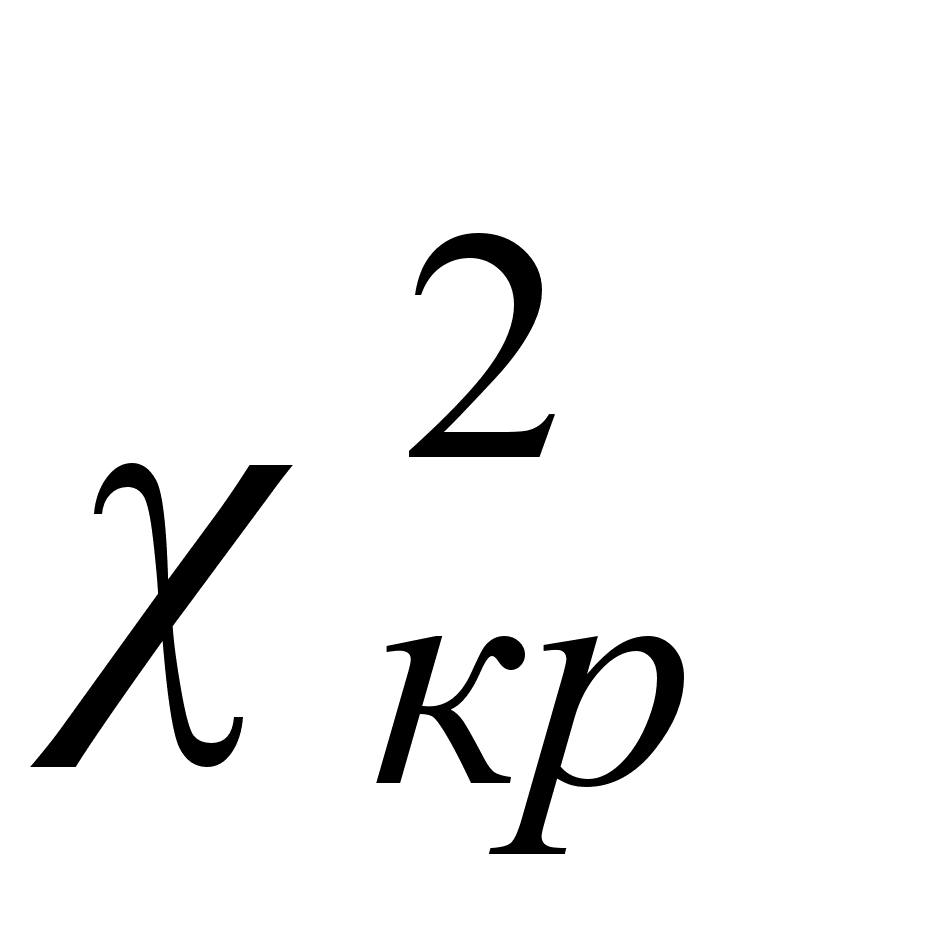для уровня значимости α = 0,05.

Таблица 5- Зависимость результирующей переменной

от факторных переменных

х1	х2	х3	у
1,1	1,1	1,2	26,2
1,4	1,5	1,1	25,9
1,7	1,8		32,5
1,7	1,7	1,8	31,7
1,8	1,9	1,8	31,7
1,8	1,8	1,9	33,6
1,9	1,8		34,2
	2,1	2,1	34,4
2,3	2,4	2,5	35,5
2,5	2,5	2,4	36,5

Если расчетное значения критерия будет больше табличного значения

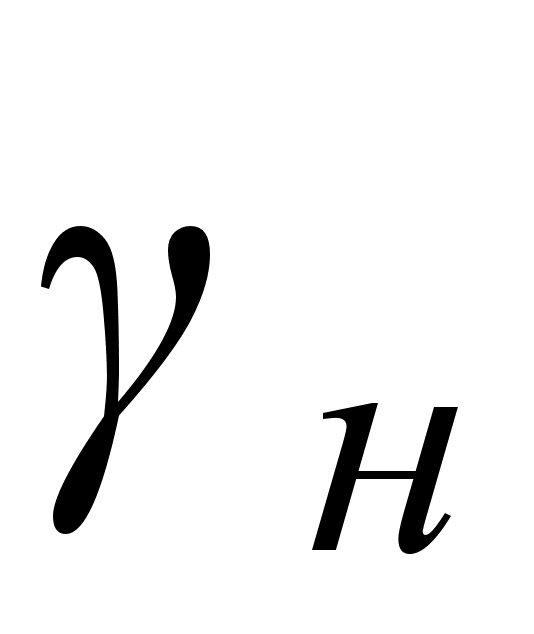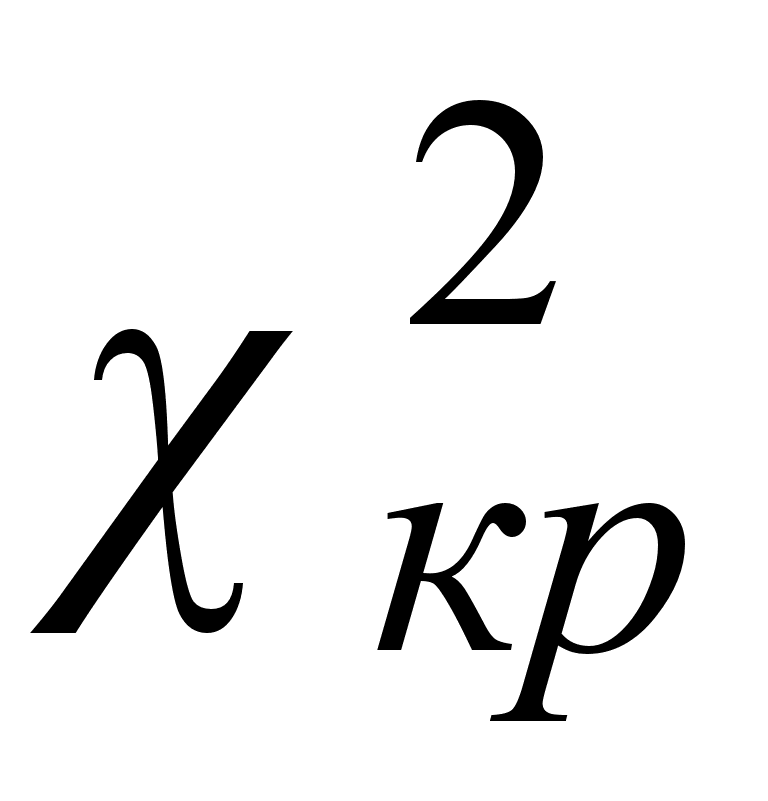> , то гипотеза Н₀ отвергается и принимается альтернативная Н₁: 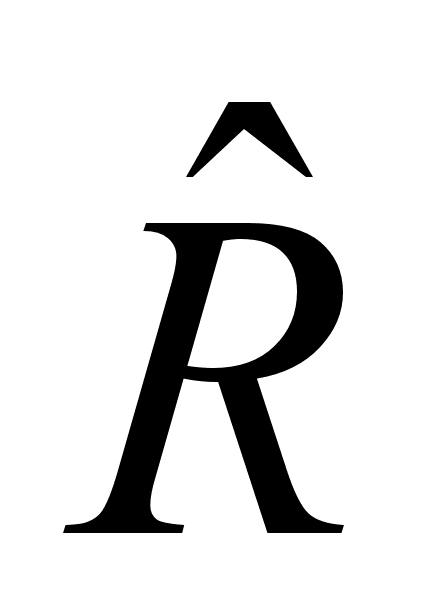значима, следовательно, имеет смысл проводить компонентный анализ.

Затем поверяется гипотеза о диагональности ковариационной матрицы.

Выдвигается нулевая гипотеза:

Н₀: соv 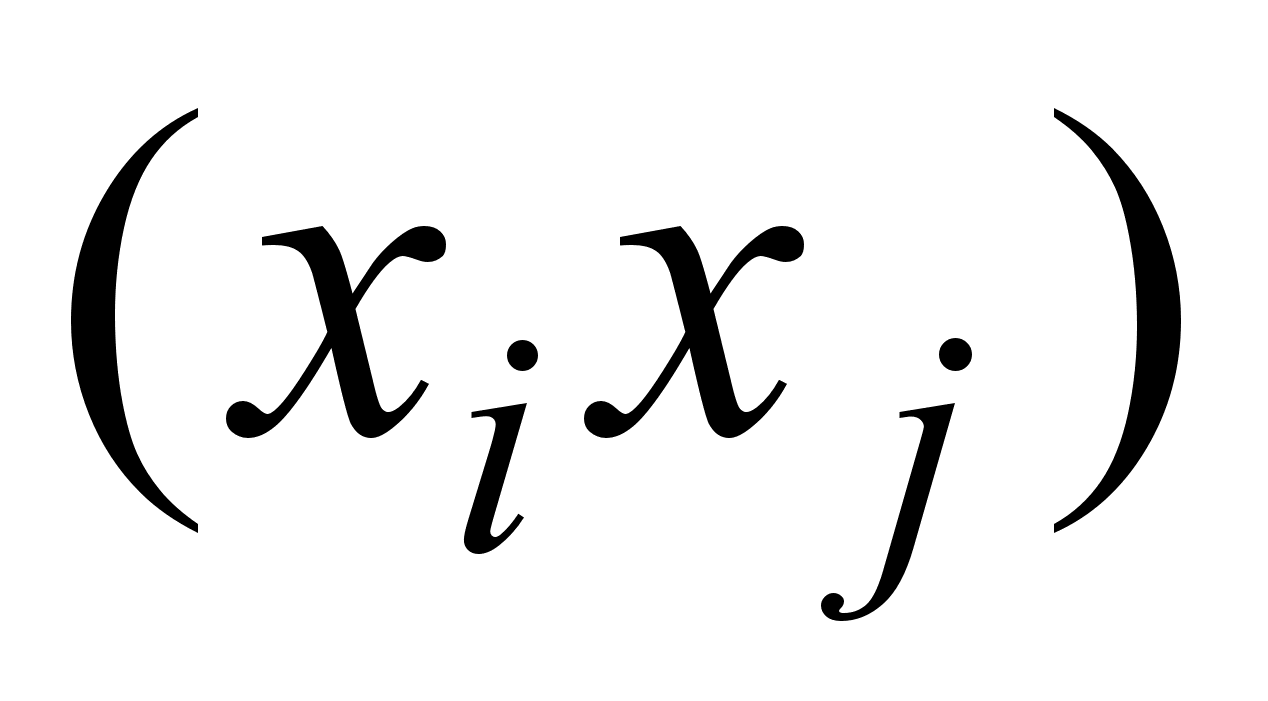=0, 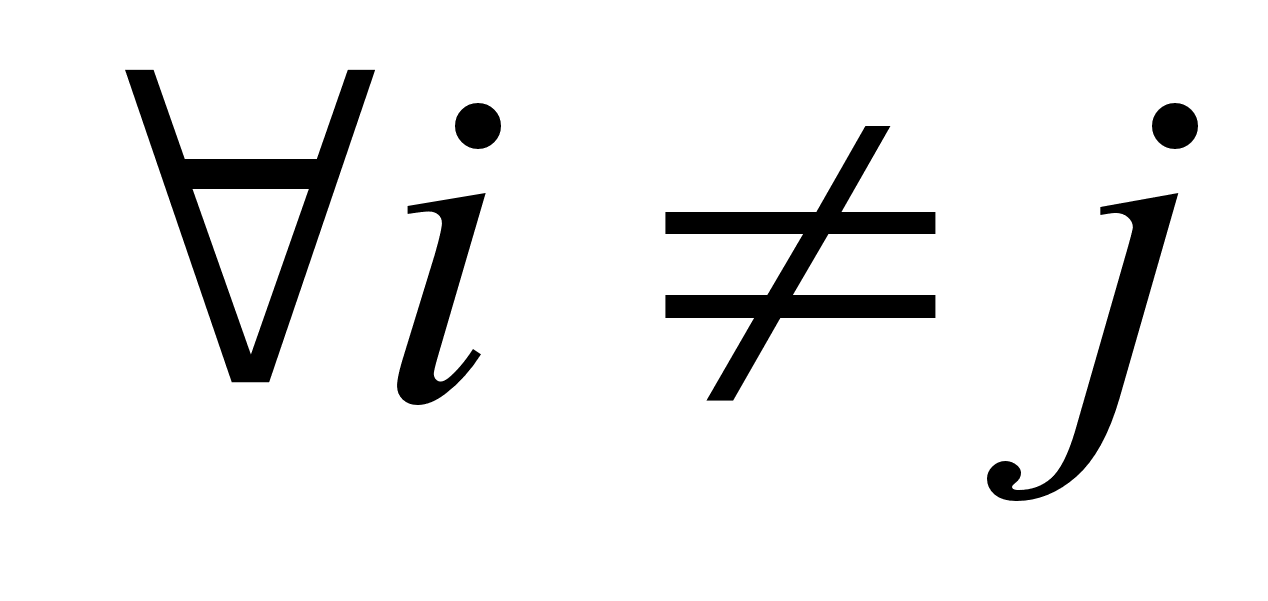и альтернативная Н₁: соv .

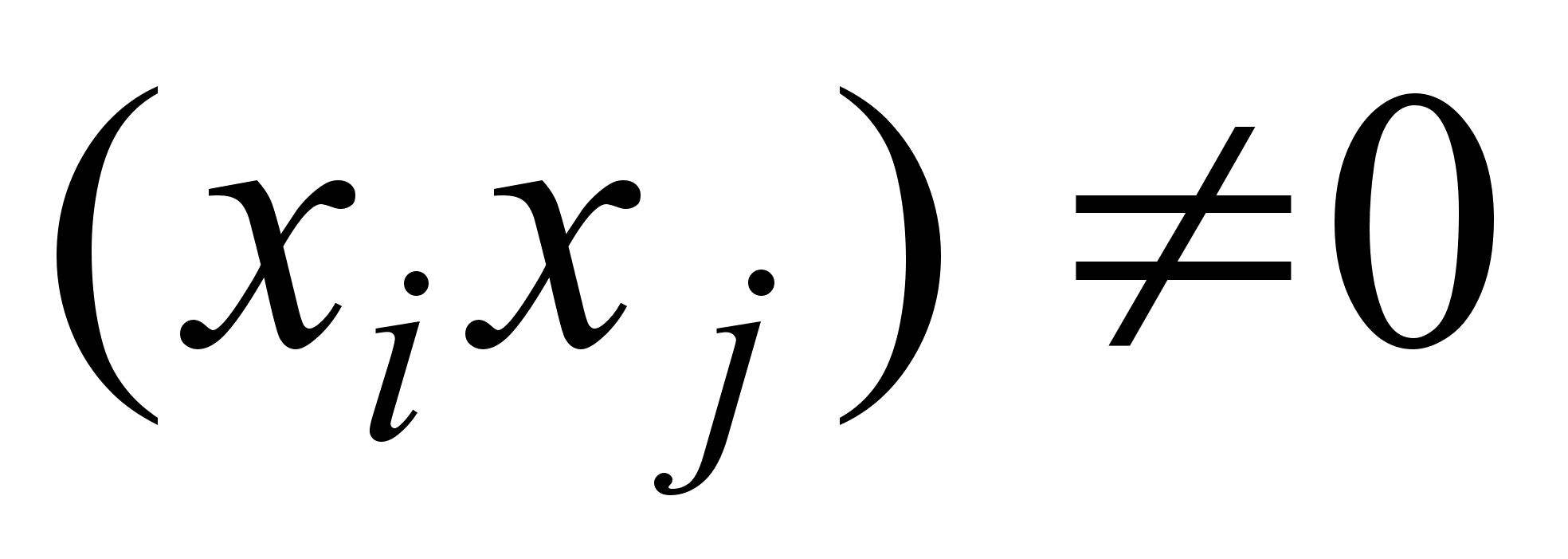Рассчитывается статистика 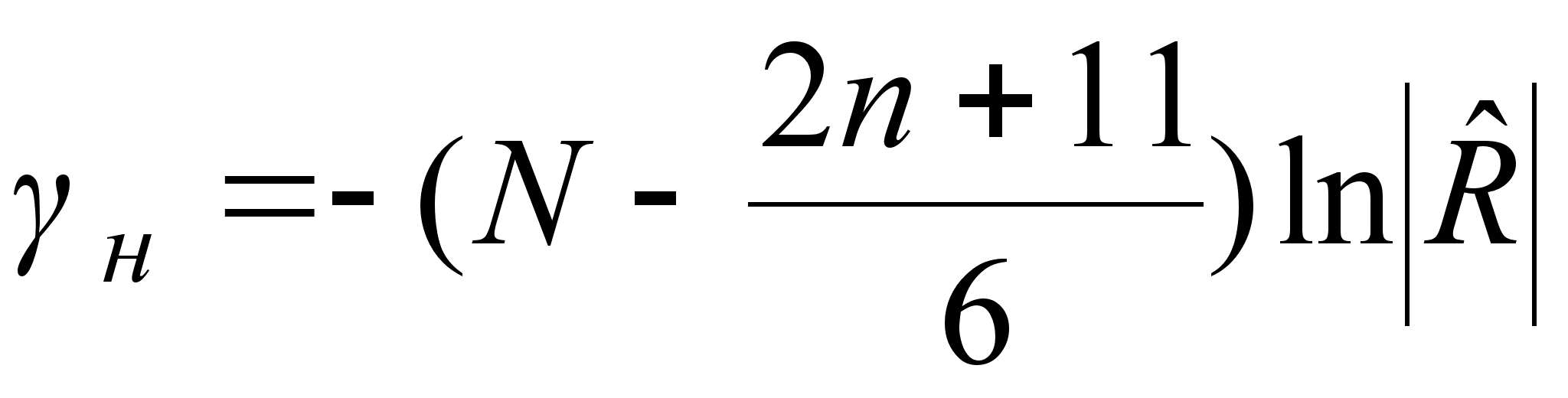, которая распределяется по закону 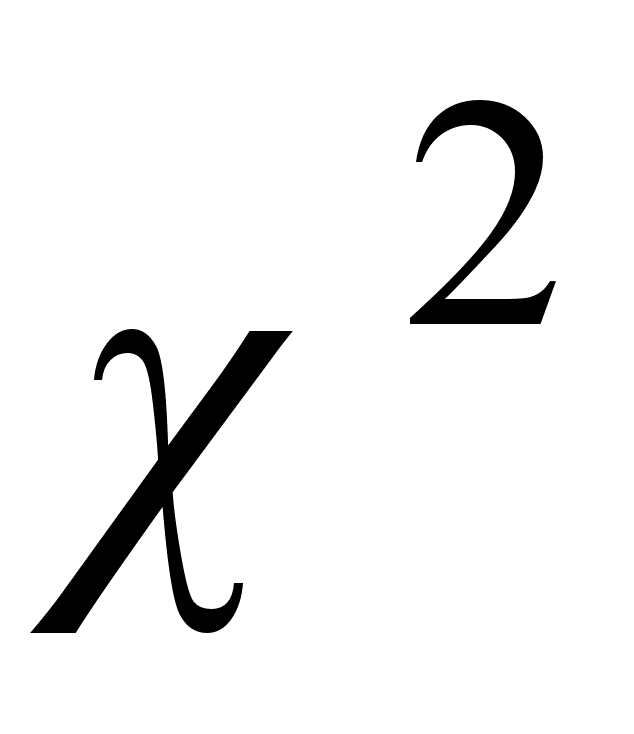с 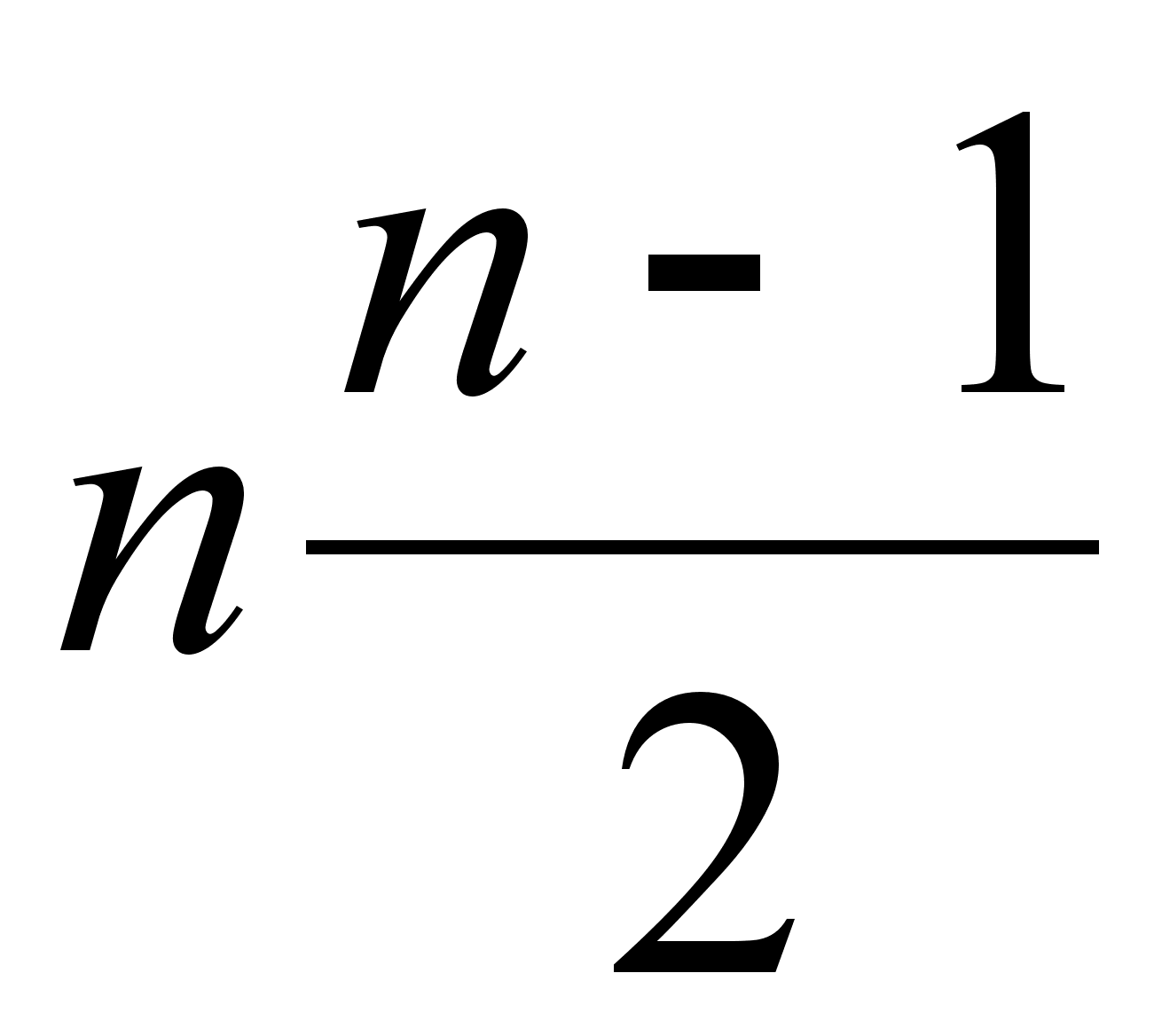степенями свободы.

Если расчетное значения критерия будет больше табличного значения

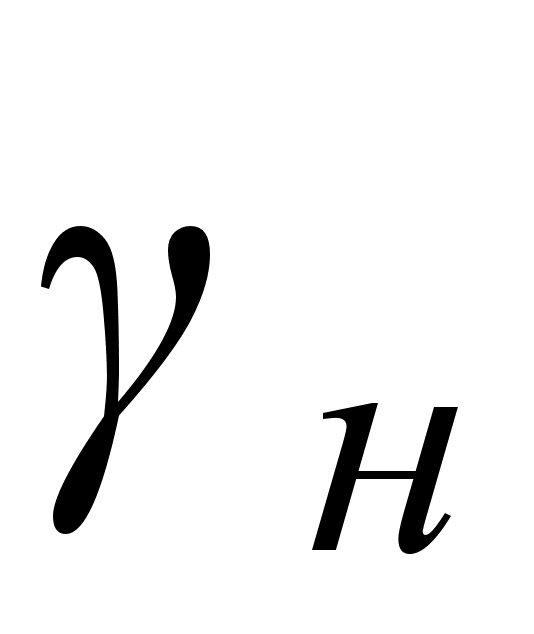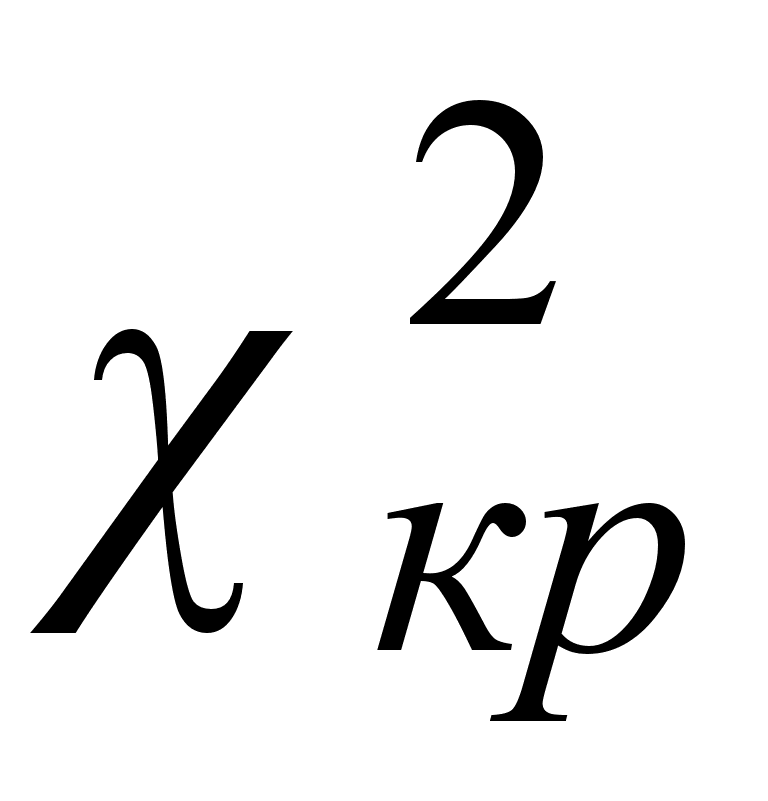> , то гипотеза Н₀ отвергается и принимается альтернативная Н₁: 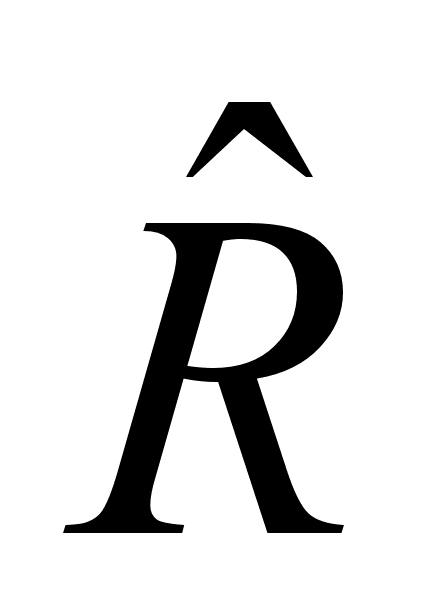значима, что подтверждает мультиколлениарность данных, следовательно имеет смысл проводить компонентный анализ.

Анализ данных (табл.5) выявил значимую коррелированность переменных x₁ – x₃, что подтверждает целесообразность проведения компонентного анализа.

Компонентный анализ проводим с использованием ППП Statgraphics Plus. Для получения данных компонентного анализа вызываем подменю Tabular optionsипомечаем окно Analysis Summaru. Результаты анализа приведены в таблице 6.

Principal Components Analysis -------------------------------------------------- Component Percent of Cumulative Number Eigenvalue Variance Percentage 1 2,888 96,26 96,26 2 0,0985 3,28 99,54 3 0,0137 0,45 100,00 --------------------------------------------------

Таблица 6- Главные компоненты

На уровне информативности 95% и выше выделяется одна главная компонента. Она имеет наибольшую дисперсию, равную 96,26%. Использование второй главной компоненты не приводит к существенному увеличению дисперсии (всего на 3,28%).

Программа рассчитывает значения главных компонент для всех опытных данных. Используя значения главных компонент строим регрессионное уравнение:

y = 32,22 + 2,00 z1.

Первая главная компонента z₁ адекватно описывает зависимую переменную y. Коэффициент детерминации равен R² = 89,34%, статистически значим при уровне значимости 0,05. Стандартная ошибка модели равна 1,25.

Факторный анализ

Факторный анализ служит для выявления и обоснования действия различных признаков и их комбинаций на исследуемый процесс путем снижения их размерности [5]. Такая задача решается, как правило, путем "сжатия" исходной информации и выделения из нее наиболее "существенной" информации. Объект описывается меньшим числом обобщенных признаков, называемых факторами.

При использовании методов факторного анализа решаются следующие задачи:

- отыскание скрытых, но объективно существующих закономерностей исследуемого процесса, определяемых воздействием внутренних и внешних причин;

- описание изучаемого процесса значительно меньшим числом факторов по сравнению с первоначально взятым количеством признаков;

- выявление первоначальных признаков, наиболее тесно связанных с основными факторами;

- прогнозирование процесса на основе уравнения регрессии, построенного по полученным факторам.

Несколько иначе осуществляется исследование латентных переменных в случае применения факторного анализа. Здесь каждая реальная переменная рассматривается также как линейная комбинация ряда факторов Fj , но в несколько необычной форме:

X _i = S B _ji · Fj + D _i.

причем суммирование ведется по j=1…m , т.е. по каждому фактору.

Здесь коэффициент B_ji принято называть нагрузкой на j-й фактор со стороны i-й переменной, а последнее слагаемое D _i рассматривать как помеху, случайное отклонение для X_i.Число факторов m вполне может быть меньше числа реальных переменных n и ситуации, когда мы хотим оценить влияние всего одного фактора (ту же вежливость продавцов), здесь вполне допустимы.

Обратим внимание на само понятие “латентный”, скрытый, непосредственно не измеримый фактор. Конечно же, нет прибора и нет эталона вежливости, образованности, выносливости и т.п. Но это не мешает нам самим “измерить” их — применив соответствующую шкалу для таких признаков, разработав тесты для оценки таких свойств по этой шкале и применив эти тесты к тем же продавцам.

Так в чем же тогда “ненаблюдаемость”? А в том, что в процессе эксперимента (обязательно) массового мы не можем непрерывно сравнивать все эти признаки с эталонами. Нам приходится брать предварительные, усредненные, полученные совсем не в “рабочих” условиях данные.

Можно отойти от экономики и обратиться к спорту. Кто будет спорить, что результат спортсмена при прыжках в высоту зависит от фактора — “сила толчковой ноги”. Да, это фактор можно измерить и в обычных физических единицах (ньютонах или бытовых килограммах), но когда?! Не во время же прыжка на соревнованиях!

А ведь именно в это, рабочее время фиксируются статистические данные, накапливается материал для исходной матрицы.

Несколько более сложно объяснить сущность самих процедур факторного анализа простыми, элементарными понятиями (по мнению некоторых специалистов в области факторного анализа — вообще невозможно). Поэтому постараемся разобраться в этом, используя достаточно сложный, но, к счастью, доведенный в практическом смысле до полного совершенства, аппарат векторной или матричной алгебры.

До того как станет понятной необходимость в таком аппарате, рассмотрим так называемую основную теорему факторного анализа. Суть ее основана на представлении модели факторного анализа в матричном виде:

X [k·1] = B [k·m] · F [m·1] + D [k·1]

и на последующем доказательстве истинности выражения

R [k·k] = B [k·m] · B^т[m·k],

для “идеального” случая, когда невязки Dпренебрежимо малы.

Здесь B^т[m·k]это та же матрица B [k·m], но преобразованная особым образом (транспонированная).

Трудность задачи отыскания матрицы нагрузок на факторы очевидна — еще в школьной алгебре указывается на бесчисленное множество решений системы уравнений, если число уравнений больше числа неизвестных. Грубый подсчет говорит, что нам понадобится найти k·m неизвестных элементов матрицы нагрузок, в то время как известно около k² / 2 коэффициентов корреляции. Некоторую “помощь” оказывает доказанное в теории факторного анализа соотношение между данным коэффициентом парной корреляции (например, R₁₂) и набором соответствующих нагрузок факторов:

R₁₂ = B₁₁ · B₂₁ + B₁₂ · B₂₂ + … + B_1m · B_2m .

Таким образом, нет ничего удивительного в том утверждении, что факторный анализ (а, значит, и системный анализ в современных условиях) — больше искусство, чем наука. Здесь менее важно владеть “навыками” и крайне важно понимать как мощность, так и ограниченные возможности этого метода.

Есть и еще одно обстоятельство, затрудняющее профессиональную подготовку в области факторного анализа — необходимость быть профессионалом в “технологическом” плане, в нашем случае в предметной области.

Но, с другой стороны, стать профессионалом высокого уровня вряд ли возможно, не имея хотя бы представлений о возможностях анализировать и эффективно управлять системами на базе решений, найденных с помощью факторного анализа.

Не следует обольщаться обещаниями популяризаторов факторного анализа, не следует верить мифам о его всемогущности и универсальности. Этот метод “на вершине” только по одному показателю — своей сложности, как по сущности, так и по сложности практической реализации даже при “повальном” использовании компьютерных программ.

Контрольные вопросы

1. Какие подходы Вы знаете к решению задач, в которых используются статистические данные?

2. Что показывает матрица ковариации и в каком анализе она используется?

3. Что показывает матрица корреляции и в каком анализе она используется?

4. В чем заключается идея метода компонентного анализа?

5. Когда имеет смысл проводить компонентный анализ?

6. Для чего служит факторный анализ?

7. В чем заключается идея метода факторного анализа?