Приложения векторного произведения в геометрии
1. Условие коллинеарности векторов.
Если 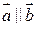 , то
, то 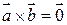 (и наоборот), т.е.
(и наоборот), т.е.
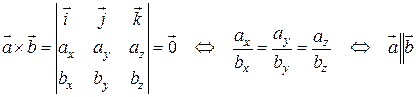 .
.
2. Нахождение площади параллелограмма и треугольника.
Согласно определению векторного произведения векторов 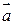 и
и 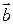
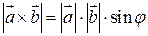 , т.е.
, т.е. 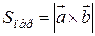 . И, значит,
. И, значит, 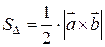 .
.
Пример 4.3. Даны векторы 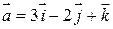 и
и 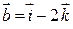 . Найти:
. Найти:
1) вектор 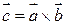 . Будут ли вектора
. Будут ли вектора 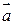 и
и 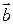 коллинеарными?
коллинеарными?
2) высоту параллелограмма, построенного на векторах 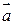 и
и 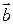 .
.
Решение. 1) Согласно формуле (4.3) находим вектор  :
:
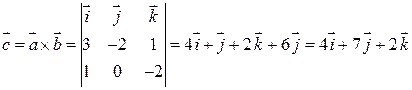 .
.
Таким образом, 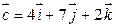 .
.
Так как 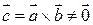 , то вектора
, то вектора 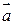 и
и 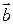 не коллинеарны.
не коллинеарны.
2) Рассмотрим параллелограмм ABCD, построенного на векторах 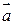 и
и 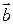 , где
, где  . BH – высота параллелограмма, которая находится по следующей формуле:
. BH – высота параллелограмма, которая находится по следующей формуле:
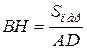 ,
,
где  - площадь параллелограмма, AD – основание параллелограмма.
- площадь параллелограмма, AD – основание параллелограмма.
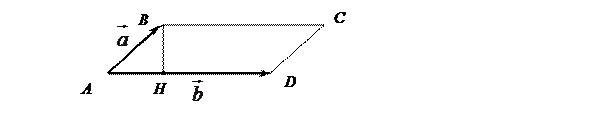
По определению векторного произведения 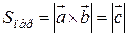 . Значит,
. Значит,
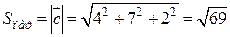 .
.
Находим  .
.
Следовательно,  .
.
,
Приложения векторного произведения в физике
1. Определение момента силы относительно точки.

Заметим, что величина 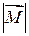 момента
момента 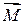 не зависит от точки A приложения силы
не зависит от точки A приложения силы  на ее линии действия AB. В самом деле,
на ее линии действия AB. В самом деле,
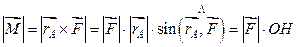 ,
,
где OH – перпендикуляр к AB. Величина OH от точки A не зависит.
2. Определение линейной скорости вращения.

3. Определение силы, действующей на проводник с током.
Известно, что магнитное поле действует как на отдельно движущиеся заряды, так и на проводники, по которым проходит электрический ток. При этом установлено, что сила  , с которой однородное магнитное поле действует на прямолинейный проводник длиной l с током
, с которой однородное магнитное поле действует на прямолинейный проводник длиной l с током  , определяется законом Ампера
, определяется законом Ампера 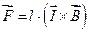 , где
, где  – вектор магнитной индукции, характеризующий силовое воздействие магнитного поля.
– вектор магнитной индукции, характеризующий силовое воздействие магнитного поля.
Пример 4.4. К точке 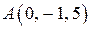 приложены три силы
приложены три силы  ,
, 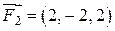 и
и 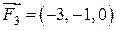 . Найти модуль момента равнодействующей этих сил относительно точки
. Найти модуль момента равнодействующей этих сил относительно точки 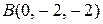 .
.
Решение. Сначала находим равнодействующую трех данных сил по формуле 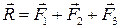 . Тогда
. Тогда
 .
.
Поскольку в условии задачи рассматривается момент равнодействующей сил относительно точки  , то находим координаты радиус-вектора точки
, то находим координаты радиус-вектора точки  , т.е. координат вектора
, т.е. координат вектора 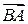 . Тогда
. Тогда  .
.
Далее находим момент силы 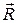 относительно точки
относительно точки  , т.е.
, т.е. 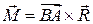 :
:
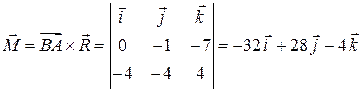 .
.
Модуль момента силы находим по формуле (2.3):
 . ,
. ,
5. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
Смешанное произведение векторов и его свойства
Определение 5.1. Смешанным (векторно-скалярным) произведением трех векторов называется число, обозначаемое 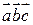 , равное скалярному произведению вектора
, равное скалярному произведению вектора 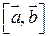 и вектора
и вектора  , т.е.
, т.е.
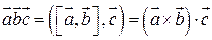 . (5.1.)
. (5.1.)
Выясним геометрический смысл смешанного произведения. В пространстве 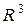 каждая тройка некомпланарных векторов
каждая тройка некомпланарных векторов 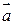 ,
, 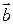 и
и  , приложенных к одной точке определяет параллелепипед, ребра которого являются эти векторы.
, приложенных к одной точке определяет параллелепипед, ребра которого являются эти векторы.

правой тройки векторов и 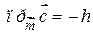 для левой. Получаем
для левой. Получаем
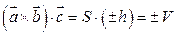 ,
,
где V – объем параллелепипеда, образованного векторами 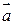 ,
, 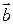 и
и  .
.
Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятых со знаком «+», если эти векторы образуют правую тройку, и со знаком «-», если они образуют левую тройку.
