Дифференциальное исчисление функции одной переменной (1 час)
Контрольная работа
1. Найти производные следующих функций:
1. 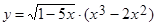 . | 2.  . |
3.  . | 4.  . |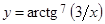
5.  . | 6.  . |
2. Заменяя приращение функции дифференциалом, найти приближенное значение 
.
Мини-опрос на лекции (35-45 мин) (30 баллов)
1. Понятие дифференцируемости функции в точке. Связь с существованием производной.
2. Наклонная асимптота графика функции 
задается уравнением вида …
3. Вычислить предел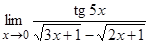 
.
4. Значение производной первого порядка функци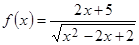и 
при 
равно …
5. Приближенное значение выражения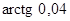 
, найденное заменой приращения функции дифференциалом, равно…
6. Если 
, то коэффициент 
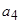разложения данной функции по формуле Тейлора по степеням 
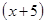равен …
Неопределенный интеграл
Контрольная работа
Найти интегралы:
1. 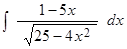 .  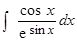. | 2.  . |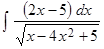
3. 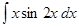 ;  . | 4.  . |
5. 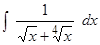 . | 6.  . |
Определенный интеграл
Контрольная работа
1. Вычислить определенные интегралы:
a)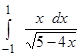 
;
b) 
.
2. Найти площадь фигуры, заключенной между линиями:
.
3. Найти длину дуги кривой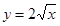 
, заключенной между точками с абсциссам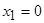и 
и 
.
4. Вычислить несобственный интеграл или установить его расходимость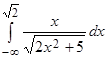 
.
5. Вычислить производную 
при значении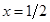 
: 
.
Ряды
Контрольная работа
1. Пользуясь определением, найти сумму ряда
.
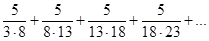2. Используя необходимое условие сходимости ряда, выяснить, является ли ряд 
сходящимся.
3. Исследовать сходимость следующих рядов:
a) 
;
b)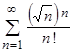 
;
c)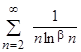 
;
d)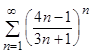 
.
4. Исследовать на абсолютную и условную сходимость ряды:
a) 
;
b)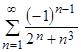 
;
c) 
.
5. Найти область сходимости степенного ряда 
.
6. Разложить функцию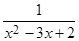 
в ряд Тейлора по степеням 
, найти область сходимости полученного ряда.
7. Найти сумму ряда 
с точностью 0,0001.
Функции нескольких переменных
Контрольная работа
1. Найти в точке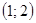 
производную функции 
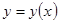, заданной неявно: 
.
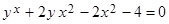2. Заменяя приращение функции дифференциалом, приближенно вычислить 
.
3. Найти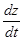 
, если 
.
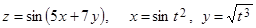4. Найти разность 
для функции 
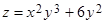в точке 
при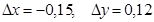 
.
5. Найти локальные экстремумы функции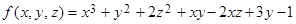 
.
6. Написать уравнение плоскости, касательной к поверхности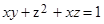 
, параллельной плоскости 
.
7. Исследовать на условный экстремум функцию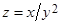 
, если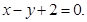 
8. Найти производную функции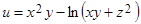 
в точке 
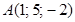по направлению вектора 
где 
Дифференциальные уравнения
Контрольная работа
1.Найти общий интеграл (общее решение) ДУ:
.
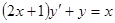2. Найти частный интеграл (частное решение) ДУ:
a) 
, 
;
3. Решить ДУ высших порядков:
a)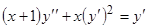 
, 
, 
.
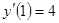4. Решить ЛДУ:
a)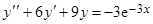 
.
Примерные контрольные кейсы
Не предусмотрено
8.3.4. Перечень примерных вопросов для зачета
Не предусмотрено
8.3.5. Перечень примерных вопросов для экзамена
Курс, 1 семестр
1. Принцип математической индукции. Вывести формулу бинома Ньютона.
2. Определение точных верхней и нижней граней числового множества. Теорема о существовании точной верхней грани ограниченного непустого числового множества.
3. Понятие функции, инъекции, биекции и сюръекции.
4. Понятие сложной и обратной функций.
5. Предел числовой последовательности. Определение расходящейся последовательности.
6. Теорема о единственности предела сходящейся последовательности.
7. Ограниченность сходящейся последовательности.
8. Теорема о предельном переходе в неравенствах.
9. Бесконечно малые и бесконечно большие последовательности. Их свойства.
10. Теорема о пределе суммы, произведения и частного сходящихся последовательностей.
11. Теорема о сохранении знака сходящейся последовательности.
12. Теорема о пределе промежуточной последовательности.
13. Монотонные последовательности. Теорема Вейерштрасса о сходимости монотонной и ограниченной последовательности.
14. Число е (и его иррациональность).
15. Предел функции в точке по Коши и по Гейне.
16. Первый замечательный предел для функций.
17. Предел функции в бесконечности. Второй замечательный предел для функций.
18. Односторонние пределы. Теорема о существовании предела функции в точке.
19. Бесконечно малые и бесконечно большие функции (примеры). Их свойства.
20. Свойства пределов функции в точке: теорема о единственности предела; теорема об ограниченности функции, имеющей предел; теорема о неравенстве пределов; теорема о промежуточной функции.
21. Арифметические свойства пределов функции.
22. Теорема о пределе композиции.
23. Сравнение функций. Теоремы об эквивалентных функциях.
24. Непрерывность функции в точке и на отрезке. Свойства непрерывных функций.
25. Теорема о непрерывности сложной функции.
26. Классификация точек разрыва (с примерами).
27. Первая теорема Вейерштрасса (об ограниченности функции, непрерывной на отрезке).
28. Понятие односторонней непрерывности. Вторая теорема Вейерштрасса (о достижении точных верхней и нижней граней непрерывной на отрезке функции).
29. Теорема Больцано-Коши о нуле непрерывной функции. Ее следствия.
30. Производная функции в точке. Геометрический смысл.
31. Понятие дифференцируемости функции в точке. Связь с существованием производной и со свойством непрерывности функции в точке.
32. Правила вычисления производных суммы; произведения и частного.
33. Дифференцирование сложной функции.
34. Дифференцирование обратной функции. Формулы для производных обратных тригонометрических функций.
35. Понятие первого дифференциала. Геометрический смысл. Дифференциал и приближенные вычисления.
36. Инвариантность формы первого дифференциала.
37. Производные высших порядков. Формула Лейбница.
38. Дифференциалы высших порядков.
39. Монотонность функции в точке и на множестве. Достаточное условие монотонности функции в точке.
40. Определение точки локального экстремума. Теорема Ферма (необходимое условие локального экстремума).
41. Теорема Ролля о среднем. Геометрический смысл.
42. Теорема Лагранжа о среднем. Геометрический смысл.
43. Теорема Коши (обобщение формулы конечных приращений).
44. Правило Бернулли-Лопиталя.
45. Формула Тейлора для многочленов.
46. Формула Тейлора с остаточным членом в форме Пеано. Формула Тейлора для элементарных функций.
47. Различные формулировки достаточных условий локального экстремума функции в точке.
48. Понятие выпуклости функции в терминах секущей к графику. Необходимое и достаточное условие выпуклости (в терминах первой производной).
49. Понятие точки перегиба. Теорема о необходимом и достаточном условиях существования точки перегиба.
50. Асимптоты. Правило нахождения наклонных асимптот.
51. Первообразная и ее связь с неопределенным интегралом. Свойства неопределенного интеграла. Теорема о существовании неопределенного интеграла. Таблица интегралов.
52. Методы вычисления неопределенного интеграла: интегрирование по частям, замена переменной, интегрирование функций, содержащих квадратный трехчлен. (Задачи).
53. Интегрирование рациональных (дробных) функций. (Задачи).
54. Интегрирование тригонометрических функций. Рационализирующие подстановки. (Задачи).
Курс, 2 семестр
1. Определенный интеграл, интегральная сумма. Определение определенного интеграла. Геометрический смысл Пример функции, не интегрируемой по Риману.
2. Ограниченность интегрируемой функции.
3. Теорема об интегрируемости непрерывной функции.
4. Теорема об интегрируемости монотонной функции.
5. Нулевая мера Жордана. Теорема об интегрируемости функции, имеющей конечное число точек разрыва.
6. Свойства интегралов от неотрицательных функций.
7. Теорема об оценке модуля интеграла.
8. Теорема о среднем для определенного интеграла.
9. Непрерывность интеграла с переменным верхним пределом.
10. Дифференцируемость интеграла с переменным верхним пределом.
11. Существование первообразной у непрерывной функции. Связь определенного и неопределенного интегралов.
12. Формула Ньютона –Лейбница.
13. Формула интегрирования по частям для определенного интеграла.
14. Замена переменных в определенном интеграле.
15. Несобственные интегралы с бесконечными пределами интегрирования. Критерий Коши сходимости несобственного интеграла.
16. Абсолютно и условно сходящиеся несобственные интегралы. Признаки сравнения сходимости несобственных интегралов.
17. Топологические понятия в 
. Последовательности в . Лемма о покоординатной сходимости.
18. Предел функции в точке. Повторные пределы. Достаточные условия равенства повторных пределов (Задачи).
19. Понятия непрерывности функции в точке, на множестве. Теорема о непрерывности дифференцируемой функции.
20. Дифференцируемость функции нескольких переменных в точке. Теорема о существовании частных производных у дифференцируемой функции.
21. Достаточное условие дифференцируемости функции двух переменных.
22. Сложная функция нескольких переменных, ее дифференцирование.
23. Дифференциал функции нескольких переменных. Его использование для приближенного вычисления значений функций и для линеаризации функций.
24. Производная по направлению. Свойства градиента. Линии и поверхности уровня.
25. Теорема о равенстве вторых смешанных производных.
26. Частные производные и дифференциалы высших порядков. Инвариантность формы первого дифференциала.
27. Формула Тейлора с остаточным членом в форме Пеано (Задачи).
28. Задачи оптимизации. Локальный экстремум ФНП. Стационарные точки. Необходимое условие существования точек локального экстремума.
29. Достаточное условие точек локального экстремума в терминах второго дифференциала.
30. Классическая задача на условный экстремум. Необходимые и достаточные условия существования локального условного экстремума в терминах функции Лагранжа. Геометрический смысл необходимых условий локального условного экстремума (Задачи).
31. Неявные функции (определение, примеры). Теоремы о дифференцировании неявных функций.
32. Глобальный экстремум. Схема его отыскания. Геометрическая интерпретация задачи оптимизации для функции двух переменных (Задачи).
33. Понятие числового ряда. Частичные суммы. Сумма ряда. Необходимый признак сходимости ряда. Пример, показывающий, что он не является достаточным.
34. Необходимое условие сходимости ряда. Свойства сходящихся рядов.
35. Числовые ряды с неотрицательными членами. Признаки сравнения рядов.
36. Признаки Даламбера и Коши сходимости числовых рядов.
37. Интегральный признак сходимости знакоположительных рядов.
38. Условная и абсолютная сходимости знакопеременных рядов.
39. Теорема Лейбница для знакочередующихся рядов. Оценка остатка ряда.
40. Функциональные последовательности. Поточечная и равномерная сходимость функциональной последовательности. Критерий Коши равномерной сходимости.
41. Функциональный ряд. Сходимость и равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости функционального ряда.
42. Степенные ряды. Формула Коши-Адамара. Радиус и интервал сходимости степенного ряда.
43. Равномерная сходимость степенного ряда. Свойства суммы. Теоремы о почленном интегрировании и дифференцировании степенного ряда.
44. Разложение функций в степенные ряды.
45. Разложение элементарных функций в ряд Тейлора.
46. Измеримые по Жордану множества. Множество меры нуль в смысле Жордана. Мера Жордана измеримого множества.
47. Определение кратного интеграла по измеримому множеству. Свойства кратных интегралов.
48. Теорема о сведении кратного интеграла к повторному.
49. Замена переменных в кратном интеграле. Полярные, цилиндрические и сферические координаты.