Системы линейных уравнений общего вида.
МАТРИЦЫ
Оглавление.
1. Определение матриц.
2. Квадратные матрицы.
3. Действия с матрицами
4. Ранг матрицы.
5. Обратная матрица.
Системы линейных уравнений.
А. Метод Гаусса.
6.б. Формулы Крамера.
6.в. Матричный метод.
Системы линейных уравнений общего вида.
Определение матриц
Прямоугольная таблица, содержащая 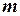 строк и
строк и 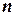 столбцов, называется матрицей размера
столбцов, называется матрицей размера 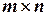 .
.
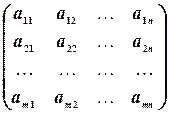
Числа 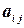 называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй — номер столбца, в котором расположен этот элемент.
называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй — номер столбца, в котором расположен этот элемент.
Матрицы обозначают буквами  ,
, 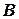 ,
, 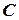 и т. д. Например,
и т. д. Например,
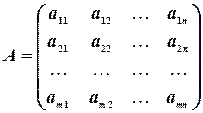
или сокращенно в виде 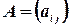
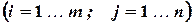 .
.
Две матрицы 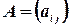 и
и 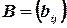 считаются равными, если равно число их строк и число столбцов и если равны элементы, стоящие на соответствующих местах этих матриц равны, то есть
считаются равными, если равно число их строк и число столбцов и если равны элементы, стоящие на соответствующих местах этих матриц равны, то есть 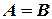 , если
, если 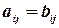 .
.
Часто приходится рассматривать матрицу, столбцами которой являются строки матрицы  . Эта матрица называется транспонированной к
. Эта матрица называется транспонированной к  и обозначается через
и обозначается через 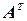 .
.
Пусть дана матрица  . Переставим строки со столбцами. Получим матрицу
. Переставим строки со столбцами. Получим матрицу
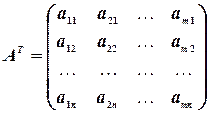 ,
,
которая будет транспонированной по отношению к матрице  .
.
Квадратные матрицы
Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число ее строк, равное числу столбцов, — порядком квадратной матрицы.
Множество всех элементов квадратной матрицы, которые лежат на отрезке, соединяющем ее левый верхний угол с правым нижним, т. е. совокупность элементов 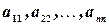 называется главной диагональю, а множество всех элементов, которые лежат на отрезке, соединяющем ее правый верхний угол с левым нижним, - побочной диагональю.
называется главной диагональю, а множество всех элементов, которые лежат на отрезке, соединяющем ее правый верхний угол с левым нижним, - побочной диагональю.
Квадратная матрица называется треугольной, если ее элементы, которые находятся над главной диагональю или под главной диагональю, равны нулю, т. е. матрицы вида
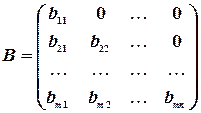 ,
, 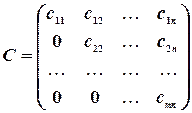
являются треугольными. Матрица 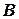 называется треугольной снизу, а матрица
называется треугольной снизу, а матрица 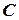 — треугольной сверху.
— треугольной сверху.
Квадратная матрица называется диагональной, если ее элементы, которые находятся вне ее главной диагонали, равны 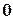 .
.
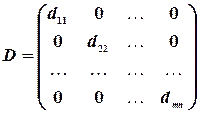 .
.
Действия с матрицами
Свойства определителя матрицы.
1. Определитель не меняется при транспонировании.
2. Если в определителе переставить две строки, определитель поменяет знак.
3. Определитель, содержащий две одинаковые строки, равен нулю.
4. Определитель, содержащий две пропорциональные строки, равен нулю.
5. Если все элементы  строки определителя представлены в виде суммы двух слагаемых
строки определителя представлены в виде суммы двух слагаемых  , то определитель равен сумме определителей, у которых все строки, кроме
, то определитель равен сумме определителей, у которых все строки, кроме  , - такие же, как в заданном определителе, а
, - такие же, как в заданном определителе, а 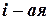 строка в одном из слагаемых состоит из элементов
строка в одном из слагаемых состоит из элементов 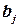 , в другом - из элементов
, в другом - из элементов 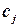 .
.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Ранг матрицы
Рассмотрим прямоугольную матрицу  . Если в этой матрице выделить произвольно
. Если в этой матрице выделить произвольно  строк и
строк и  столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу
столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу 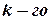 порядка. Определитель этой матрицы называется минором k-го порядкаматрицы
порядка. Определитель этой матрицы называется минором k-го порядкаматрицы  . Очевидно, что матрица
. Очевидно, что матрица  обладает минорами любого порядка от
обладает минорами любого порядка от 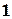 до наименьшего из чисел
до наименьшего из чисел 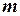 и
и 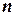 . Некоторые среди них будут равны нулю. Среди всех отличных от нуля миноров матрицы
. Некоторые среди них будут равны нулю. Среди всех отличных от нуля миноров матрицы  найдется, по крайней мере, один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы
найдется, по крайней мере, один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы  равен
равен 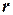 , то это означает, что в матрице
, то это означает, что в матрице  имеется отличный от нуля минор порядка
имеется отличный от нуля минор порядка 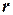 , но всякий минор порядка, большего чем
, но всякий минор порядка, большего чем 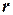 , равен нулю. Ранг матрицы
, равен нулю. Ранг матрицы  обозначается через
обозначается через 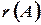 . Очевидно, что выполняется соотношение
. Очевидно, что выполняется соотношение
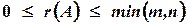
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор 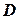
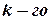 порядка матрицы
порядка матрицы  , отличный от нуля, то требуют вычисления лишь миноры
, отличный от нуля, то требуют вычисления лишь миноры 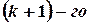 порядка, окаймляющие минор
порядка, окаймляющие минор 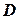 , т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен
, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен  .
.
Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы  и
и 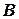 эквивалентны, то это записывается так:
эквивалентны, то это записывается так:  .
.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,
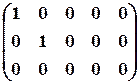 .
.
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Пример 11. Найти методом окаймления миноров ранг матрицы
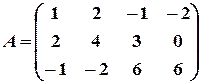
Решение. Начинаем с миноров  порядка, (т.е. с элементов матрицы
порядка, (т.е. с элементов матрицы  ). Выберем, например, минор (элемент)
). Выберем, например, минор (элемент) 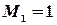 , расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор
, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор 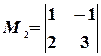 , отличный от нуля. Переходим теперь к минорам
, отличный от нуля. Переходим теперь к минорам 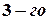 порядка, окаймляющим
порядка, окаймляющим 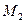 . Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:
. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:
 ,
, 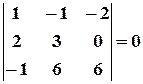 .
.
Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы  равен двум.
равен двум.
Пример 12. Найти ранг матрицы
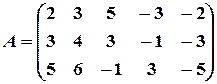
и привести ее к каноническому виду.
Решение. Из второй строки вычтем первую и переставим эти строки:
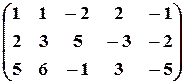 .
.
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 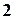 и
и  :
:
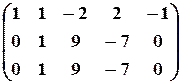 ;
;
из третьей строки вычтем вторую, при этом получим матрицу
 ,
,
которая эквивалентна матрице  , так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы
, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы 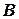 равен
равен 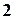 , а следовательно, и
, а следовательно, и 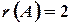 .
.
Матрицу 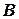 легко привести к канонической.
легко привести к канонической.
Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются.
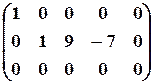
Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:
. 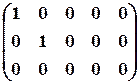
Обратная матрица
Пусть дана квадратная матрица:
 .
.
Обозначим  .
.
Квадратная матрица  называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если
называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если 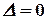 .
.
Квадратная матрица 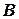 называется обратной для квадратной матрицы
называется обратной для квадратной матрицы  того же порядка, если их произведение
того же порядка, если их произведение  , где
, где 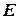 - единичная матрица того же порядка, что и матрицы
- единичная матрица того же порядка, что и матрицы  и
и 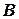 .
.
Теорема. Для того чтобы матрица  имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице  , обозначается через
, обозначается через 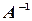 , так что
, так что 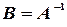 . Обратная матрица вычисляется по формуле
. Обратная матрица вычисляется по формуле
 ,
,
где 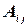 - алгебраические дополнения элементов
- алгебраические дополнения элементов 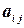 . Или
. Или

Таким образом, обратная матрица – это транспонированная матрица алгебраических дополнений, умноженная на коэффициент 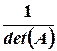 .
.
Вычисление обратной матрицы по этой формуле для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП).
Любую неособенную матрицу  путем ЭП только столбцов (или только строк) можно привести к единичной матрице
путем ЭП только столбцов (или только строк) можно привести к единичной матрице 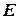 .
.
Если совершенные над матрицей  ЭП в том же порядке применить к единичной матрице
ЭП в том же порядке применить к единичной матрице 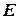 , то в результате получится обратная матрица. Удобно совершать ЭП над матрицами
, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами  и
и 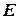 одновременно, записывая обе матрицы рядом через черту.
одновременно, записывая обе матрицы рядом через черту.
Замечание. Отметим, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример 15. Для матрицы  найти обратную ей матрицу.
найти обратную ей матрицу.
Решение. Находим сначала детерминант матрицы  (для этого прибавляем ко второму столбцу первый, а от третьего отнимаем первый, деленный на два):
(для этого прибавляем ко второму столбцу первый, а от третьего отнимаем первый, деленный на два):
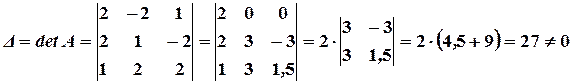
значит, обратная матрица существует, и мы ее можем найти по формуле:
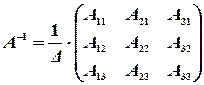 ,
,
где 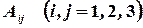 ‑ алгебраические дополнения элементов
‑ алгебраические дополнения элементов 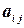 исходной матрицы.
исходной матрицы.
 ,
,  ,
,
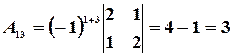 ,
,  ,
,
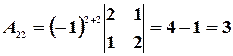 ,
, 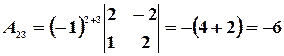 ,
,
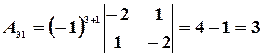 ,
, 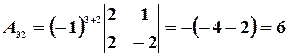 ,
,
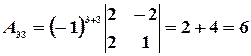
Откуда

 .
.
Пример 16. Методом элементарных преобразований найти обратную матрицу для матрицы: 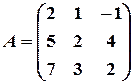 .
.
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: 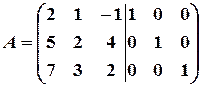 . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
. С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
1. Поменяем местами первый и второй столбцы:
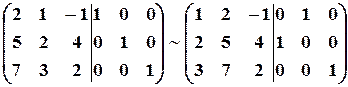 .
.
2. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на 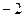 :
:
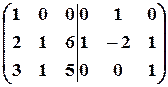 .
.
3. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на  второй;
второй;
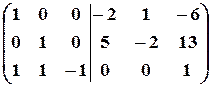 .
.
4. Прибавим третий столбец к первому и второму:
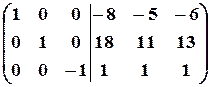 .
.
5. Умножим последний столбец на  :
:
 .
.
Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице  . Итак,
. Итак,
 .
.
Системы линейных уравнений.
Система линейных уравнений имеет вид:
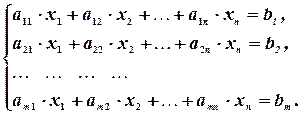
Здесь 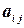 и
и 
 ‑ заданные, а
‑ заданные, а  ‑ неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему в виде:
‑ неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему в виде:
AX =B
где 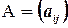 - матрица, состоящая из коэффициентов при неизвестных, которая называется матрицей системы,
- матрица, состоящая из коэффициентов при неизвестных, которая называется матрицей системы, 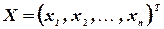 ,
, 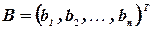 - векторы-столбцы, составленные соответственно из неизвестных
- векторы-столбцы, составленные соответственно из неизвестных  xj и из свободных членов bi.
xj и из свободных членов bi.
Упорядоченная совокупность 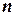 вещественных чисел
вещественных чисел 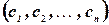 называется решением системы, если в результате подстановки этих чисел вместо соответствующих переменных
называется решением системы, если в результате подстановки этих чисел вместо соответствующих переменных 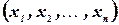 каждое уравнение системы обратится в арифметическое тождество.
каждое уравнение системы обратится в арифметическое тождество.
Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.
Матрица
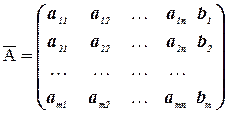 ,
,
образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.
Вопрос о совместности системы решается следующей теоремой.
Теорема Кронекера-Капелли.
Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и 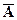 совпадают, т.е.
совпадают, т.е. 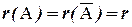 .
.
Система имеет единственное решение только в том случае, когда
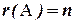 . При этом число уравнений - не меньше числа неизвестных
. При этом число уравнений - не меньше числа неизвестных  ; если
; если 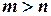 , то
, то  уравнений являются следствиями остальных. Если
уравнений являются следствиями остальных. Если 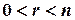 , то система является неопределенной.
, то система является неопределенной.
Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:
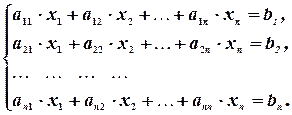
Эти системы решаются одним из следующих способов:
1) методом Гаусса, или методом исключения неизвестных;
2) по формулам Крамера;
3) матричным методом.
Пример 17. Исследовать систему уравнений и решить ее, если она совместна:

Решение. Выписываем расширенную матрицу системы:
 .
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу 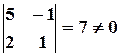 ; содержащие его миноры третьего порядка равны нулю:
; содержащие его миноры третьего порядка равны нулю:
 ,
, 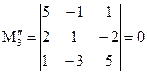 .
.
Следовательно, ранг основной матрицы системы равен 2, т.е.  . Для вычисления ранга расширенной матрицы
. Для вычисления ранга расширенной матрицы 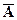 рассмотрим окаймляющий минор
рассмотрим окаймляющий минор
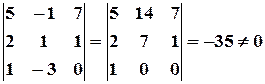 ,
,
значит, ранг расширенной матрицы 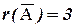 . Поскольку
. Поскольку  , то система несовместна.
, то система несовместна.
А. Метод Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных, данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 18. Решить систему уравнений методом Гаусса:

Решение. Выпишем расширенную матрицу данной системы
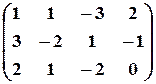
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
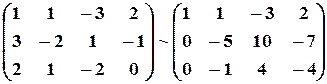 ;
;
б) третью строку умножим на (-5) и прибавим к ней вторую:
 .
.
В результате всех этих преобразований данная система приводится к треугольному виду:
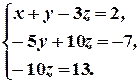
Из последнего уравнения находим  . Подставляя это значение во второе уравнение, имеем
. Подставляя это значение во второе уравнение, имеем 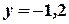 . Далее из первого уравнения получим
. Далее из первого уравнения получим 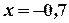 .
.
Б. Формулы Крамера
Назовем столбцы матрицы  следующим образом: первый столбец -
следующим образом: первый столбец - 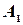 , второй столбец -
, второй столбец - 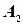 , и т.д., последний столбец -
, и т.д., последний столбец -  . Тогда матрицу
. Тогда матрицу 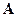 можно записать в виде
можно записать в виде 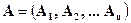 .
.
Составим 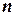 дополнительных матриц:
дополнительных матриц:
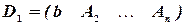 ,
,  , …,
, …, 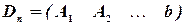 ,
,
и вычислим их определители и определитель исходной матрицы:
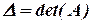 ,
,  ,
,  , …,
, …,  .
.
Тогда значения неизвестных вычисляются по формулам Крамера:
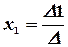 ,
, 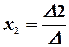 , …,
, …, 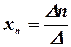 .
.
Правило Крамера дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по вышеприведенным формулам.
Если главный определитель системы 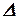 и все вспомогательные определители
и все вспомогательные определители 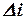 равны нулю, то система имеет бесчисленное множество решений.
равны нулю, то система имеет бесчисленное множество решений.
Если главный определитель системы  , а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Пример 19. Решить систему уравнений методом Крамера.

 ,
, 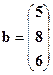 .
.
Тогда
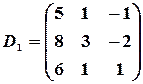 ,
, 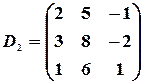 ,
, 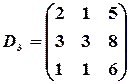 .
.
Вычисляя определители этих матриц, получаем 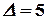 ,
,  ,
, 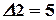 ,
, 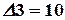 .
.
И по формулам Крамера находим: 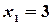 ,
,  ,
, 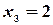 .
.
В. Матричный метод
Теперь, рассмотрим матричное уравнение 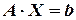 . Если у матрицы
. Если у матрицы  существует обратная матрица
существует обратная матрица 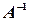 , то, умножая матричное уравнение на
, то, умножая матричное уравнение на 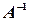 слева, получим:
слева, получим:
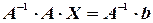 .
.
По определению обратимости матрицы  и по свойству единичной
и по свойству единичной 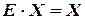 , получаем:
, получаем:
 .
.
Пример 20. Решить систему уравнений с помощью обратной матрицы.
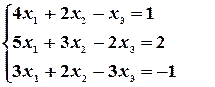
Имеем:
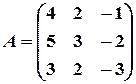 ,
, 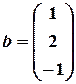 .
.
Вычислим определитель матрицы 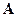 , разлагая по первой строке:
, разлагая по первой строке:

Значит, обратная матрица существует. Вычислим алгебраические дополнения элементов матрицы:
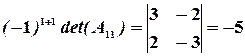 ,
,  ,
,
 ,
,  ,
,
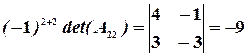 ,
,  ,
,
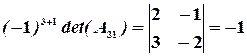 ,
, 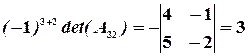 ,
,
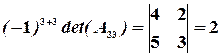 .
.
Тогда решение системы получается умножением обратной матрицы на столбец свободных членов

МАТРИЦЫ
Оглавление.
1. Определение матриц.
2. Квадратные матрицы.
3. Действия с матрицами
4. Ранг матрицы.
5. Обратная матрица.
Системы линейных уравнений.
А. Метод Гаусса.
6.б. Формулы Крамера.
6.в. Матричный метод.
Системы линейных уравнений общего вида.
Определение матриц
Прямоугольная таблица, содержащая 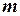 строк и
строк и 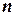 столбцов, называется матрицей размера
столбцов, называется матрицей размера 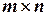 .
.
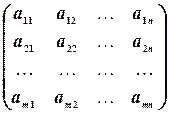
Числа 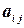 называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй — номер столбца, в котором расположен этот элемент.
называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй — номер столбца, в котором расположен этот элемент.
Матрицы обозначают буквами  ,
, 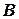 ,
, 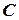 и т. д. Например,
и т. д. Например,
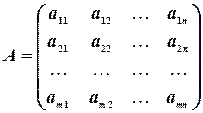
или сокращенно в виде 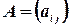
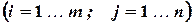 .
.
Две матрицы 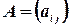 и
и 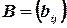 считаются равными, если равно число их строк и число столбцов и если равны элементы, стоящие на соответствующих местах этих матриц равны, то есть
считаются равными, если равно число их строк и число столбцов и если равны элементы, стоящие на соответствующих местах этих матриц равны, то есть 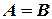 , если
, если 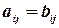 .
.
Часто приходится рассматривать матрицу, столбцами которой являются строки матрицы  . Эта матрица называется транспонированной к
. Эта матрица называется транспонированной к  и обозначается через
и обозначается через 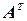 .
.
Пусть дана матрица  . Переставим строки со столбцами. Получим матрицу
. Переставим строки со столбцами. Получим матрицу
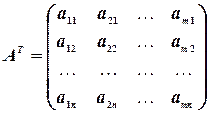 ,
,
которая будет транспонированной по отношению к матрице  .
.
Квадратные матрицы
Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число ее строк, равное числу столбцов, — порядком квадратной матрицы.
Множество всех элементов квадратной матрицы, которые лежат на отрезке, соединяющем ее левый верхний угол с правым нижним, т. е. совокупность элементов 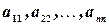 называется главной диагональю, а множество всех элементов, которые лежат на отрезке, соединяющем ее правый верхний угол с левым нижним, - побочной диагональю.
называется главной диагональю, а множество всех элементов, которые лежат на отрезке, соединяющем ее правый верхний угол с левым нижним, - побочной диагональю.
Квадратная матрица называется треугольной, если ее элементы, которые находятся над главной диагональю или под главной диагональю, равны нулю, т. е. матрицы вида
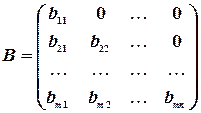 ,
, 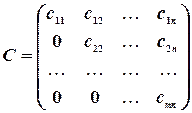
являются треугольными. Матрица 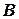 называется треугольной снизу, а матрица
называется треугольной снизу, а матрица 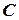 — треугольной сверху.
— треугольной сверху.
Квадратная матрица называется диагональной, если ее элементы, которые находятся вне ее главной диагонали, равны 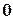 .
.
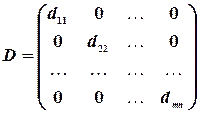 .
.
Действия с матрицами
