Недетерминированные конечные автоматы-распознаватели.

Важную роль в теории автоматов и формальных языков играют недетерминированные конечные автоматы-распознаватели (НКА), которые являются более общим классом автоматов-распознавателей, включающий в себя и класс детерминированных автоматов.

Отличае НКА от ДКА заключается в том, что у НКА есть возможность совершать переходы по пустой цепочке ε, т.е. спонтанно, не получая на вход никакого символа. Кроме того, в НКА возможны несколько переходов, помеченных одним и тем же символом. Такие способности работы НКА часто трактуются как возможность делать «догадки» относительно входных данных.

Определение. Недетерминированным конечным автоматом-распознавателем называется автомат с конечным непустым входным алфавитом Х, с конечным непустым множеством состояний S, с начальным состоянием S_oϵS, работа которого описывается характеристической функцией переходов δ:S×(XUε)→2^S, где 2^S – есть булеан X, т.е. множество всех подмножеств множества X, и FϵS, где F – множество финальных состояний.

Таким образом, работа НКА описывается пятеркой: A={ X, S, S_o, δ, F}.

Рассмотрим пример НКА. На рис. приведен автомат с ε-переходами и всеми возможными переходами при подаче на его вход цепочки 1110.

Находясь в начальном состоянии S_o, автомат может спонтанно, без подачи какого-либо сигнала, перейти в состояние S₁. Этот переход на графе обозначен через ε. Если на вход подать символ 1, автомат перейдет из состояния S_o в состояние S₂. Из состояния S₂ автомат может перейти под воздействием символа 1 в любое из состояний S₂ и S₃, при этом из состояния S₃ он может спонтанно перейти опять в состояние S₂.

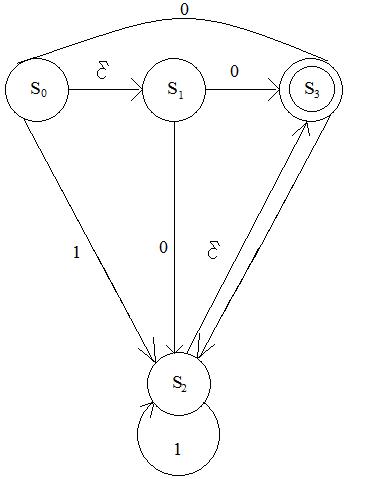
Рис. 5.6. НКА с ε-переходоми и возможное его поведение при подаче цепочки 1101.

В связи с возможностями спонтанных переходов и переходов в несколько состояний, встает вопрос о том, какие входные цепочки распознает НКА.

Определение. НКА распознает входную цепочку, если существует путь, помеченный символами цепочки а, из начального в одно из заключительных состояний автомата, возможно, с учетом спонтанных переходов. НКА распознает язык L, если он распознает все цепочки этого языка, и только их.

НКА, представленный на рис. распознает входную цепочку 1110, т.к. под воздействием этой цепочки НКА переходит из начального состояния S_o в финальное состояние S₃. С другой стороны, рассматриваемый НКА не допускает ни пустой цепочки ε, ни цепочки 010.

В том случае, когда из некоторого состояния автомата не существует перехода под действием конкретного символа, принадлежащего цепочке а, говорят, что автомат «зависает» и не может далее функционировать. Для НКА, приведенного на рис. , из состояния S₁ нет перехода при поступлении символа 1, следовательно, автомат так и останется в этом состоянии S₁ – «зависнет».

Утверждение. Недетерминированный конечный автомат распознает входную цепочку а, если существует путь, помеченный символами цепочки а, из начального состояния в одно из заключительных состояний автомата, возможно, с учетом спонтанных переходов.

Из приведенного утверждения следует, что любой язык, который допускается детерминированным автоматом, допускается и недетерминированным, так как множество недетерминированных автоматов включает в себя множество детерминированных автоматов. Верно и обратное утверждение.

Теорема. Для каждого недетерминированного автомата существует эквивалентный детерминированный автомат, который допускает тот же язык.

Вместо формального доказательства, приведем пример построения детерминированного автомата, который допускает язык, допустимый недетерминированным автоматом.

На первом этапе покажем, как привести НКА к автомату без ε-переходов.

Пусть А_ε={ X, S, S_o, δ_ε, F } – НКА с ε-переходами, при чем δ_ε:S×(XUε)→2^S. Требуется привести данный НКА к детерминированному автомату А={X,S,q_o,δ,F} без ε-переходов. Для этого введем понятие ε-замыкания.

Определение. ε-замыканием состояния sϵS, обозначаем σ(s), называется множество всех состояний, которые достижимы из состояния S по спонтанным переходам (без подачи входного сигнала).

Множеству σ(s) принадлежит как само состояние S, так и все состояния, достижимые из S по ε-переходами. Для НКА, приведенного на рис. σ(s_o)={S_o,S₁}, σ(s₁)={S₁}, σ(s₂)={S₂}, σ(s₃)={S₃,S₂}.

Множеством начальных состояний автомата А являются

S_o=Uσ(s): все состояния, достижимые из любого начального состояния без подачи входного сигнала, которые так же, очевидно, являются начальными. Для автомата, изображенного на рис. начальными состояниями являются σ(s_o) и σ(s₁).

Множеством заключенных состояний А являются такие ε-замыкания состояний автомата А_ε, в которые входят заключительные состояния А_ε: из каждого такого состояния без подачи входного сигнала можно оказаться в заключительном состоянии. В нашем случае множество заключительных состояний {σ(s₃)}.

Выполнив ε-замыкания, получаем, что функция переходов δ автомата А запишется так:

( σ(s))( aϵX)δ(σ(s), a)=U(σ(s), a).

Иначе говоря, при воздействии входного сигнала а автомат А переходит из ε-замыкания состояния S в ε-замыкание всех тех состояний S, в которые автомат А_ε переходит под воздействием сигнала а из всех состояний, достижимых из S под воздействием ε.

Составим таблицу переходов эквивалентного недетерминированного автомата без ε-переходов (табл.5.1).

Таблица.5.1

	а	b
So= σ(so)	{ σ(s2), σ(s3)}	{ σ(s2)}
S1= σ(s1)	{ σ(s2), σ(s3)}	Ø
S2= σ(s2)	Ø	{ σ(s2), σ(s3)}
S3= σ(s3)	{ σ(so), σ(s1), σ(s2), σ(s3)}	{ σ(s2), σ(s3)}

Граф переходов, построенный по табл.5.1 приведен на рис. 5.7.

По сравнению с исходным автоматом (рис. 5.6) в построенном графе переходов добавилось еще одно начальное состояние и по паре переходов из состояний S_o и S₃.

Рис. 5.7 НКА без ε-переходов.

Преобразованный на первом этапе автомат все равно остается недетерминированным, т.к. из одного состояния возможны несколько переходов, помеченных одним и тем же символом. В нашем случае из состояния S, под воздействием символа а возможен переход как в S₂, так и в S₃. (рис.8. )

На втором этапе по полученному НКА без ε-переходов A_H={S,X,q_o,δ_H,F_H} построим эквивалентный детерминированный автомат. Отметим, что в общем случае в автомате AH множество начальных состояний может содержать несколько состояний. В нашем случае это состояния S_о и S₁ (рис. 9. ).

В качестве состояний искомого ДКА выбирается множество состояний исходного НКА, а в качестве на начального (начальных) состояния – множество начальных состояний того же НКА.

Приняв эти пояснения, ДКА определяется как A_g={2^S,X,p_o,δ_g,F_g}, а функция переходов определяется следующим образом ( PϵS)( aϵX):δ_g(P,a)=U(δ_H(Q,a)).

Множество F_g заключительных состояний искомого ДКА состоит из всех таких множеств состояний, которые включают хотя бы одно заключительное состояние преобразуемого НКА: F_g=U(Q∩F_H)=Ø.

Определив таким образом функцию переходов и множество заключительных состояний искомого ДКА, составляется таблица переходов, выявляются эквивалентные состояния и производится минимизация автомата аналогично минимизации структурных автоматов.

НА практике чаще применяется более простой алгоритм преобразования НКА без ε-переходов в эквивалентный ему ДКА.

Алгоритм преобразования НКА в ДКА.

1.Начальные состояния НКА {S_o} и ДКА {p_o} совпадают.

2. Для всех символов a_iϵQ построим переход изначального состояния p_o в множество всех состояний, достижимых из S_o.

3. Для каждого вновь построенного состояния p_j и для каждого a_iϵQ построить переход из p_j в множество достижимых из него состояний.

4. Продолжить процесс пока есть возможность создавать новые состояния.

5. Преобразовать все множество состояний S_j, содержащее множество финальных состояний НКА, в финальное состояние ДКА.

Пример. Задан НКА с начальным состоянием S_o (рис.5.8).

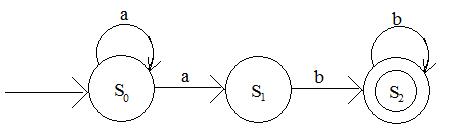
Рис. 5.8 НКА с начальным состоянием S_o.

Построим переход из состояния S_o в множество всех состояний, достижимых из этого состояния при поступлении на вход символа а. В данном случае имеется переход из S_o в S_o и из S_o в S₁, т.е. построим переход из S_o (S_o=p_o) в {S_o,S₁}=p₁ (рис.5.9). Рассмотрим переход из состояния p₁ в множество всех состояний, достижимых по символу а. В данном случае возможен переход из p₁ в p₁ и из p₁ в p₂. Из состояния p₂ возможен переход в p₂ при подаче символа b.

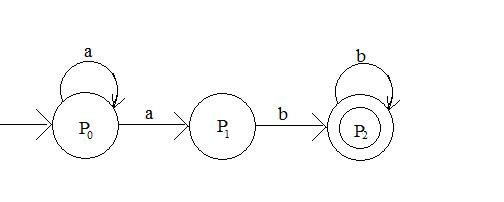
Рис. 5.9 ДКА эквивалентный НКА.

Финальное состояние ДКА состоит из всех множеств, содержащих элемент финального множества НКА. В нашем случае p₂ единственное финальное состояние.

Отметим, что подача любого символа, кроме рассмотренных (рис. 12. ) переводит автомат в состояние «зависания».

В теории формальных грамматик широко используется алгебраическое описание языков с помощью регулярных выражений, которые, в свою очередь, определяются через регулярные множества |13|.

Регулярные выражения позволяют задавать языки с помощью формул. Но и конечные автоматы обладают этим же свойством. Возникает вопрос о соотношении языков, задаваемых конечными автоматами L_A и языков, задаваемых регулярными выражениями L_p.

Американский математик Клини С.К. доказал следующую теорему.

Теорема Клини. Классы регулярных множеств и автоматных языков совпадают между собой, т.е. L_A=L_p |15|.

В качестве примеров использования регулярных выражений приведем команду поиска grep операционной системы UNIX и генератор лексического анализа LEX.

Подробно регулярные множества и регулярные выражения рассматриваются в курсах «Теория языков программирования и методы трансляции» и «Проектирование драйверов».

ЛИТЕРАТУРА

1. Чирков М.К. Основы общей теории конечных автоматов. Л.: Издат. Ленинградского Университета. 1975., 280 стр.

2. Митюшин Ф.Ф., Нагорнова В.Ф., Шаповалов Ю.В. Теория, расчет и проектирование вычислительных устройств дискретного действия. Логическое проектирование. М.: МАИ, 1973., 176стр.

3. Белоусов А.И., Ткачев О.А. Дискретная математика. М.: Издат.МГТУ им. Н.Э.Баумана, 2004.,704стр.

4. Карпов Ю.Г. Теория автоматов. Спб.: Питер, 2002., 224стр.

5. Яблонский С.В., Гаврилов Г.П., Кудрявцев В.Б. Функции алгебры логики и классы Поста. М.: Наука, 1966. 120стр.

6. Митюшин Ф.Ф., Нагорнова В.Ф., Шаповалов Ю.В. Сборник задач по вычислительной технике. Арифметические и логические основы ЦВМ. М., МАИ, 1968. 112стр.

7. Каган Б.М. Электронные вычислительные машины и системы. М.: Энергоатомиздат. 1985. 552стр.

8. Палий И.А. Дискретная математика. Курс лекций. М.:Эксмо. 2008. 352стр.

9. Гилл А. Введение в теория конечных автоматов. М.: Наука. 1966. 272стр.

10. Левин В.И. Динамика логических устройств и систем. М.: Энергия. 1980. 224стр.

11. Фридман А., Менон П. Теория и проектирование переключательных схем. М.: Мир. 1978. 581стр.

12. Миллер Р. Теория переключательных схем. Том II. М.: Наука. 1971. 304стр.

13. Хопкрофт Дж. Мотвани Р., Ульман Джер. Введение в теорию автоматов, языков и вычислений. 2-е изд. М.: издательский дом «Вильямс». 2002. 528стр.: ил.

14. Куликов В.В. Дискретная математика. М.: РИОР. 2012. 174стр.

15. Клини С.К. Представление событий в нервных сетях (сб. «Автоматы». – м.: ИЛ, 1956. – с. 15-67.

[V1]