Проблема риска не правильного срабатывания.

При синтезе как комбинационных схем, так и синхронных конечных автоматов, мы считали, что переменные х и х не могут одновременно иметь одну и ту же величину и все сигналы, представляющие эту переменную, изменяются одновременно. Для реальных схем это допущение выполняется не всегда.

Рассмотрим в качестве примера схему (рис. 4.5).

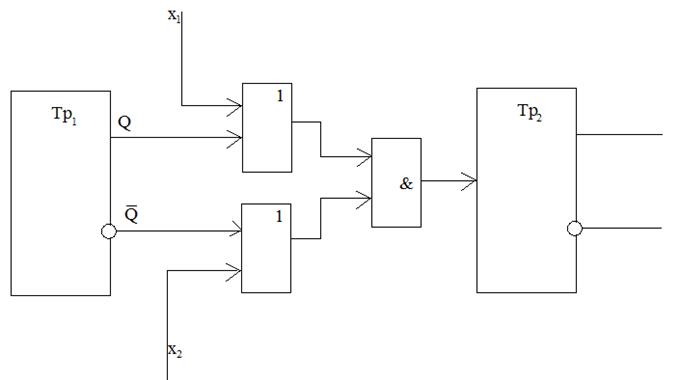
Рис.4.5. Логическая схема с риском не правильного срабатывания.

В тот момент, когда реальный триггер меняет свое состояние, возникает короткий промежуток времени, в течении которого оба выхода Тр1 воспринимается схемами «ИЛИ» как Q=Q=1. в этом случае на Тр2 поступает короткий сигнал, равный 1, который может привести к ложному срабатыванию Тр2.

С ростом быстродействия цифровых схем возрастает и риск ложных срабатываний.

Проблема устранения ложных срабатываний получила название проблема риска.

Если состояние, которое должен сохранить триггер равно единице, то говорят о риске в единице, если нулевое – о риске в нуле.

Проблема риска возникает тогда, когда схема имеет на своих входах как свою переменную, так и ее инверсию.

Различают статические и динамические риски сбоя.

Говорят, что комбинационная схема имеет статический риск сбоя, когда от схемы требуется сохранить выходное состояние постоянным в течении перехода, но при некотором распределении паразитных задержек, выходной сигнал может измениться один или четное число раз.

Говорят, что комбинационная схема имеет динамический риск сбоя, если при некотором распределении паразитных задержек на выходе схемы может возникнуть последовательность из трех или большего числа изменений выходного сигнала, тогда как должно быть только одно такое изменение. (рис. 4.6.).

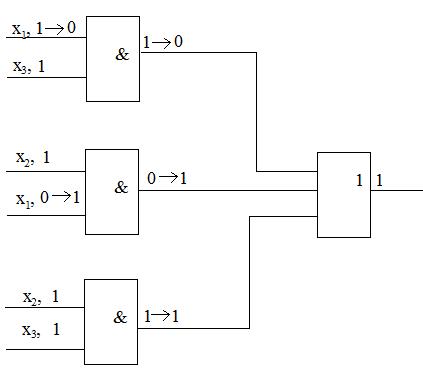
Рис. 4.6. Пример динамического риска сбоя.

Рассмотрим комбинационную схему, приведенную на рисунке 4.6

Когда входное состояние переменных х₁=х₂=х₃=1, то а=1, в=0.

При изменении переменной х₁ из единицы в ноль, сигнал а меняется из один в ноль, а сигнал в из нуля в один.

Если изменение х₁ из сигнала, равного нулю, то сигнал а будет меняться из сигнала равного один в сигнал равный нулю. В свою очередь сигнал в будет менятся из сигнала равного один в сигнал равный нулю.

Если изменение сигнала в будет происходить медленнее, чем изменение сигнала а, что может быть вызвано большей паразитной задержкой в цепи, то оба входа на элементе ИЛИ могут оказаться равными нулю в течении времени, достаточном чтобы на выходе схемы сформировался сигнал, равный нулю. А затем сигнал на выходе установится равным один.

Так как появление ложного срабатывания схемы зависит от соотношения паразитных задержек в ней, то одним из способов устранения риска сбоев является введение дополнительных задаржек для согласования работы схемы.

Рассмотрим схему, приведенную на рисунке .4.6

Для рассматриваемой схемы риск сбоя может быть устранен введением в схему дополнительного элемента И, который логически перемножает такие входные переменные, которые имеют значение единица на обоих входных комбинациях (рис. .4.7).

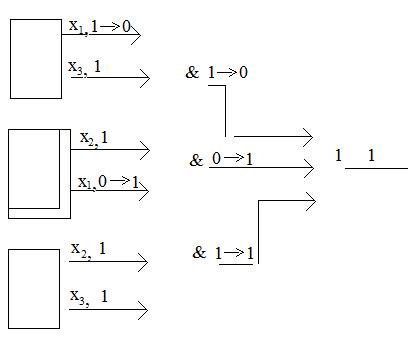
Рис. 4.7 Схема устранения риска сбоя.

Говорят, что двухуровневая комбинационная схема реализующая сумму произведений, два входных набора которой X₁={x₁, x₂, …, x_i, …, x_n} и X₂={x₁, x₂, …, x_i, …, x_n}, отличающиеся лишь одной переменной x_i и для которых f₁(X₁)=f₂(X₂)=1, имеется риск сбоя в единице при переходе от х₁ к х₂ тогда и только тогда, когда реализация этой функции не содержит произведения, которое содержит единицу для обоих наборов.

Второе правило можно сформулировать в следующем виде. Пусть f₁(X₁) и f₂(X₂) равны 0, а входные наборы Х₁ и Х₂ отличаются только одной переменной. Двухуровневая схема, реализующая сумму произведений, имеет риск сбоя в нуле при переходе от набора Х₁ к Х₂ тогда, и только тогда, когда она содержит элементарные произведения, имеющие переменные x_i и x_i, а другие переменные равны один для обоих наборов Х₁ и Х₂.

Комбинационные риски сбоя, обусловленные изменением многих переменных на входе схемы, отличаются от схем с однократным изменением входного сигнала тем, что не всегда могут быть устранены введением в схему дополнительных элементов.

В связи с ростом плотности упаковки активных элементов на одном кристалле и создание больших интегральных схем (БИС) и сверхбольших БИС, применение обычных методов синхронизации встречает ряд трудностей. Поэтому для таких схем применяют метод борьбы с гонками и рисками, получивший название метод самосинхронизации. Суть метода заключается в том, что рабочие схемы проектируются непротивогоночными, но они дополняются специальными схемами, которые фиксируют окончание переходных процессов и вырабатывают разрешающий сигнал для последующих схем, играющий роль синхросигнала. Однако, в схемах и микросхемах с обыной степенью интеграции (ИС) это направление не может быть рекомендовано ввиду, как сложности построения такого рода схем, так и приблизительно, удвоения аппаратных затрат.

Отметим, что в настоящее время в цифровой технике широко применяются интегральные схемы с потенциальным способом представления информации. Такие элеименты снижают на своем выходе разницу между уровнями нулевого и единичных сигналов, а так же искажают форму сигнала. Для устранения этих проблем в таких схемах ставят промежуточные усилители и формирователи формы сигналов.