Синтез логических схем на мультиплексорах.

Мультиплексором называют устройства, которые позволяют реализовать логическую схему любой сложности. В отличие от интегральных схем, где имеется набор элементов, обладающих большой избыточностью, мультиплексор совмещает логические функции в модуле одного типа. Так как такой модуль выполнен в виде одного кристалла интегральной схемы (ИС), то он обладает более высоким быстродействием и надежностью, облегчает проектирование и упрощает компоновку печатной платы. При изготовлении мультиплексоров, можно использовать технологию средних интегральных схем для размещения на одном кристалле законченных функциональных логических схем (счетчики, дешифраторы, сдвиговые регистры и др.). При этом один тип модуля может обеспечить проектирование различных узлов одного изделия, а также различные изделия на одном и том же типе элементов. Мультиплексор в принципе может быть реализован на любых элементах, применяемых в схемотехнике: элементы диодно-транзисторной логики, транзисторно-транзисторной логики или любой другой. В настоящее время получили распространение два типа модулей: сдвоенные четырехвходовые (рис.2.4.а) и восьмивходовые (рис.2.4.б).

Основные характеристики рассматриваемых мультиплексоров приведены в табл.2.2.

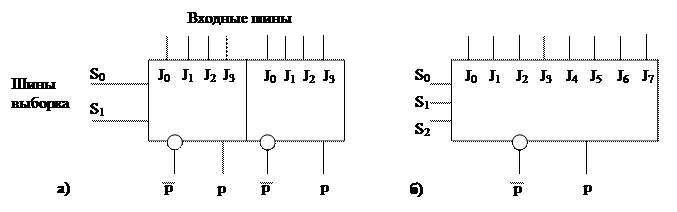
Рис.2.4.

Таблица 2.2.

Структурная схема мультиплексора приведена на рис.2.5. Эта схема собрана из элементов «И-НЕ» и имеет М=2^n-1, F=2^n-1+n+1.

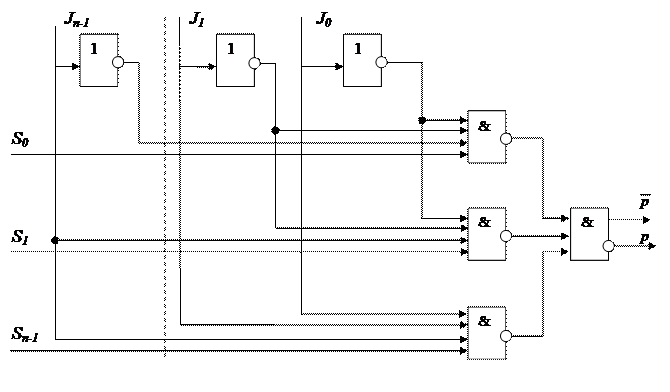Рис.2.5.

Из основных положений построения логических схем можно показать, что для реализации любой булевой функции n переменных достаточно иметь устройство, которое содержит 2^n-1 схемы, реализующие соответствующим образом подобранные 2^n-1 минтермов. Если функция обращается в единицу на числе наборов больше чем 2^n-1, то нетрудно показать, что в этом случае будут обязательно склеивающиеся минтермы и, следовательно, потребуется меньшее количество оборудования. Исходя из этих предпосылок можно организовать внутреннюю структуру мультиплексора. Половина четырехвходового мультиплексора может реализовать любую из 256 функций трех аргументов (рис.2.4,а). При этом на шины выборки подаются сигналы двух любых аргументов, а на входные шины соответствующие сигналы третьего аргумента.

Предположим, что на мультиплексорах надо реализовать один разряд комбинационного сумматора на три входа. Так как в комбинационном сумматоре необходимо иметь значение суммы в данном разряде и значение переноса в последующий старший разряд, то целесообразно использовать сдвоенный четырехвходовой мультиплексор. Булево уравнение для функции суммы будет

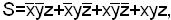
для переноса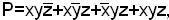

где S –сумма в данном разряде;

x, y –значения слагаемых в данном разряде;

z – перенос из предыдущего младшего разряда;

P – перенос в последующий старший разряд.

На основе булевых уравнений составляются таблицы истинности заданных функций и карты минимизации (рис.2.6,а,б).

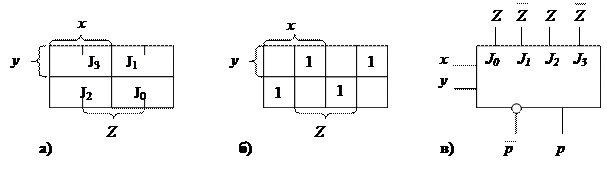
Рис.2.6.

Карта Вейча могла быть составлена и без таблицы истинности непосредственно по формуле. Таблица истинности или карта минимизации используется для определения сигналов трех переменных к мультиплексору.

Таблица 2.3

X
Y
Z
S
P

Таблица истинности (табл.2.3) показывает, что когда x и y равны 0, функция выхода S совпадает с z. Это означает, что на вход J₀ нужно подать аргумент z. Когда x=0 и y=1 (код на шинах выборки 01), внутренние логические схемы мультиплексора срабатывают таким образом, что к этой комбинации подключается вход J₁. Для этого случая таблица истинности показывает, что выход S будет равен 1 только тогда, когда z=0. Следовательно, на вход J₁ (рис.2.6,в) нужно подать дополнение z, т.е. 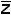. Соответственно на вход J₂ надо подать 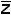и на вход J₃ - z. Это можно было определить, не прибегая к карте минимизации. Если для определения схемы подачи сигналов на входы используется карта минимизации, то требуется промежуточный этап. Карта делится на четыре двухячеечных участка, каждый из которых содержит одну ячейку для z и другую для его дополнения 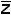и соответствует одному из четырех входов модуля. Каждый участок карты будет содержать любую из четырех возможных комбинаций единиц и нулей (00, 01, 10, 11). Порядок расположения двоичных цифр определяет, какой сигнал должен быть получен на выходе мультиплексора и, следовательно, какой сигнал нужно подать на соответствующий вход. Если участок карты имеет код 11, на выходе всегда должен быть код 1. Для этого достаточно подать на соответствующий вход постоянное напражение, принимаемое за уровень, соответствующий логической единице. Если участок имеет код 00, выход всегда будет 0 и на соответствующий вход нужно подать постоянный уровень для 0 (чаще всего потенциал земли). Комбинации 1 и 0 разобраны в предыдущем примере.

Составим логическую схему для переноса P(табл.2.3). На основании булева уравнения составим карту минимизации(рис.2.7,а). По карте минимизации составим логическую схему на половине сдвоенного четырехвходового мультиплексора (рис.2.7,б). В этой схеме на вход J₀ подается потенциал, соответствующий сигналу 0(потенциал земли). На входы J₁ и J₂ подается входной сигнал z, так как функция обращается в единицу, когда z=1 и в нуль – когда z=0; на вход J₃ подается сигнал, соответствующий единице, так как при любом значении z функция равна 1. Окончательно схема для одного разряда сумматора реализуется на одном сдвоенном четырехвходовом мультиплексоре (рис.2.8).

В целом, алгоритм определения схемы подключения сигналов ко входам мультиплексора может быть сформулирован следующим образом.

1. Составляется таблица истинности для трех переменных; определяется значение третьей переменной; берется аргумент или его отрицание или постоянные 0 или 1, которые должны быть поданы на входные шины.

2. Составляется карта минимизации; распределяются участки карты по входам J_i.

Рис.2.7. Рис.2.8

Метод использования универсальной логической схемы для функции трех переменных может быть распространен на реализацию функций четырех и более переменных. Для реализации функции четырех переменных удобнее использовать восьмивходовой мультиплексор. Покажем это на примере.

Пример. Пусть для реализации задана функция

f(ABCD)=m₂+ m₄+ m₅+ m₆+ m₉+ m₁₀+ m₁₁+ m₁₃.

Составим таблицу истинности (табл.2.4) и карты минимизации как и в предыдущем случае (рис.2.9,а,б). Каждый участок карты приписывается каждому из восьми входов мультиплексора. Требуемая схема подачи входных сигналов определяется при рассмотрении карты в зависимости от того, какой код в них содержится – 00, 01, 10 или 11. Для данной функции схема подключения входов имеет вид (рис.2.9,в):

J₀ – земля, J₁ – D, J₂ - U₀, J₃ – D, J₄ - , J₅ - U₀, J₆ - 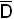, J₇ – земля.

При реализации функции от пяти и более переменных требуется более одного уровня универсальных логических схем. В этом случае один набор логических схем вырабатывает сигналы, подаваемые на другой набор схемы. Например, для реализации функций шести переменных в общем случае требуется восемь четырехвходовых мультиплексоров (4 ИС) на первом уровне и один восьмивходовой мультиплексор на втором уровне.

Таблица 2.4

A

B

C

D

f(ABCD)

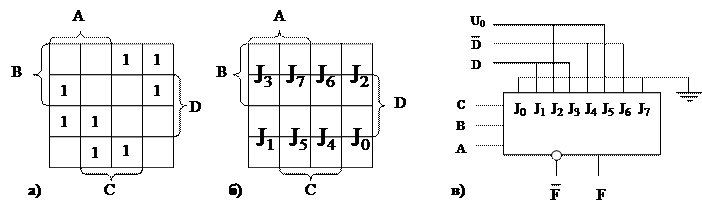
Рис.2.9.

Чтобы создать схему, реализующую функцию шести переменных f(ABCDEF), переменные функции делят на две части A,B,C и D,E,F. В этом случае схемная реализация упрощается. Вместо задачи для шести переменных получаются две задачи при трех переменных, которые решаются следующим образом:

а) выделяют каждую их комбинаций D,E,F, получают функции остальных трех переменных f_i(ABC), соответствующих каждой комбинации;

б) собирают все элементы функции f_i(ABC), соответствующие каждому отдельному виду комбинации входных сигналов D,E,F;

в) реализуют каждую функцию переменных A,B,C как функцию трех переменных, получают выходные сигналы первого уровня;

г) подают эти входные сигналы первого уровня на восьмивходовой мультиплексор, который управляется комбинациями сигналов D,E,F, поступающими на шины выборки.

Покажем это на примере функции

f(ABCDEF)=∑0,2,4,5,6,9,10,11,12,13,14,15,17,

24,25,26,28,29,30,31,32,33,37,38,39,

43,44,45,48,51,58,59,60,63.

В таблице истинности (табл.2.5) покажем только те наборы, на которых функция обращается в единицу (рис.2.10).

В некоторых случаях схема может быть упрощена перестановкой аргументов, которые должны быть включены на первом уровне. Переменные должны располагаться так, чтобы для двух или более групп J_i их значения были бы или инверсны друг другу, или имели бы одинаковые значения. В этих случаях один и тот же элемент можно использовать несколько раз (если для некоторых J_i аргументов на первом уровне принимают одинаковые значения). Если аргументы на первом уровне для некоторых значений J_i –х принимает противоположные значения, то в этом случае можно использовать инверсию от J_i –го выхода. Заданную функцию f(ABCDEF) можно реализовать путем преобразования ее в функцию 1-го уровня f(CDB) (вместо f(ABC)) и комбинацию переменных второго уровня EFA. При такой группировке значения функции f(CDB) одинаковы для членов второго уровня J₀ и J₁, а член второго уровня J₇ является дополнением J₆. В результате такой группировки для реализации заданной функции требуется на два четырехвходовых мультиплексора меньше, чем в предыдущем случае (табл.2.6).

Табл. 2.5. Табл.2.6.

Так как последовательные устройства можно рассматривать в качестве обычных логический устройств с обратными связями, то это означает, что мультиплексор может быть использован и при реализации конечных автоматов.Мультиплексоры являются основным элементом для моделирования базовых ячеек ПЛИС.

Рис.2.10

Контрольные задания.

А. Минимизировать функции методом Квайна.

1.f (А,В,С)=АВ +АВС+ АВС+АВС.

2.f (А,В,С)=АВ +С+ АВС+ВС+АВ

3.f (А,В,С)=АВС+АВ+АВС+АВСД+СД

_4. f (А,В,С,Д)=m₄+ m₅₊m₆₊m₇₊m₁₂₊m₁₄₊m₁₅

_5. f (А,В,С,Д)=m₁+ m₅+m₅+m₇+m₉+m₁₁ +m₁₃+m₁₅

Б. Минимизировать функции методом Макс-Класки

_1. f (А,В,С,Д)=m₃+ m₄+m₅+m₇+m₉+m₁₁ +m₁₃+m₁₅

2.f (А,В,С,Д)=АВД + АВСД+ АВСД+ АВСД+ АВСД

3.f (А,В,С,Д)=ВСД + АВСД+ АВСД+ АВСД+ АВСД+ АВСД

_4. f(х_1, х₂ х₃х₄ )= х₁ х₂х₃ х₄ + х₁ х₂х₃ х₄ х₅

5.f (А,В,С,Д)=АВСД + АВСД+ АВСД+ АВСД+ АВСД+ АВСД

Подсчитать количество элементов И, ИЛИ, НЕ требуемых для реализации заданных функций.

В. Минимизировать функции методом карт Вейна.

1.f (А,В,С)= АВ + АВС +АВС + АВС

2.f (А,В,С)=АВС + АВС + АВС + АВС

3.f (А,В,С)=АВС + АВС + АВС + АВС

_4. f (А,В,С,Д)=m₀+m₁+ m₄ +m₅+m₁₀+m₁₁+m₁₄+m₁₅

_5. f (А,В,С,Д)=m₄+m₅+ m₆ +m₇+m₁₂+m₁₃+m₁₄+m₁₅

Построить схемы, реализующие заданные функции на элементах И, ИЛИ, НЕ.

Г. Найти минимальные конъюнктивные формы функций.

_1. f (А,В,С)=m₅+m₃+ m₆ +m₇

_2. f(х_1, х₂ х₃ )= х₁ х₂х₃ + х₁ х₂х₃ + х₁ х₂х₃ + х₁ х₂х₃

_3. f (А,В,С,Д)=m₀+m₁+ m₂ +m₅+m₉+m₁₀+m₁₂+m₁₃ +m₁₄

Подсчитать число элементов И, ИЛИ, НЕ требуемых для реализации заданных функций.

Д. Найти минимальные формы предоставления частичных функций.

1.f (А,В,С,Д)=АВС + ДВС + АСД -если минтерм избыточен

2.f (А,В,С,Д)=m₁+m₂+ m₅ + m₆ +m₇ +m₁₀ , если минтермы m₀+m₄+ m₁₅ избыточны

3.f(х_1, х₂ х₃ х₄)= х_1, х₂ х₃ х₄ + х_1, х₂ х₃ х_{4 ,} если конъюнкция ВС избыточна.

4.f (А,В,С,Д)= m₇ +m₁₁ + m₁₃ +m₁₄ если минтерм m₁₅ избыточен.

5.f(х_1, х₂ х₃ х₄)= х_1, х₂ х₃ х₄ + х_1, х₂ х₃ х_{4 ,} если х₄ избыточен.

Е. Минимизировать системы функций.

1. f (А,В,С)= m₀+m₁+ m₃

f (А,В,С)=m₁+m₂+ m₅

f (А,В,С)=m₃+m₅ +m₇

_2. f(х_1, х₂ х₃ )= m₀+ m₂ +m₄+ m₇

f(х_1, х₂ х₃ )= m₀+m₃+m₅ +m₇

_3. f (х_1, х₂ х₃)=m₁+m₃ +m₇

f (х_1, х₂ х₃)= m₂ +m₄

f (х_1, х₂ х₃)=m₁+m₄+ m₅

Ж. Определить количество элементов И-НЕ для реализации следующих функций.

_1. f (А,В)= m₀+m₁

_2. f (А,В,С)= m₀+m₁ + m₂ +m₃ +m₄+m₅

_3. f (А,В,С,Д)= m₀+m₁ + m₂ +m₃ +m₁₂+m₁₃ + m₁₄ +m₁₅

_4. f (А,В,С,Д)= m₀+m₁ + m₂ +m₃ +m₄+m₅+m₈ + m₉

З. Построить схему на элементах И-НЕ, реализующюю функции.

1.f (А,В,С)=АВС+АВС+АВС+АВС

2.f (А,В,С,Д)=АВСД+АВСД+АВСД+АВСД+АВСД+АВСД+АВСД

3.f (х_1, х₂ х₃)=m₁+m₂+m₃ +m₄+m₅+ m₆+m₇+m₈ + m₁₁ +m₁₂ + m₁₃

И. Определить количество элементов ИЛИ-НЕ для реализации функций

_1. f (А,В,С)=М₀+М₁+М₃+М₅

2.f (А,В,С,Д)=m₀+ m₂+m₃ +m₄+m₅+ m₆ +m₉ + m₁₂ + m₁₃

_3. f (А,В,С,Д)=m₀+ m₁ + m₆+m₇ +m₈+m₉ + m₁₂ + m₁₃ + m₁₄ + m₁₅

К. Построить схему на элементах ИЛИ-НЕ для реализации функций.

_1. f (А,В,С,Д)=М₀М₃М₅М₇М₁₁

2.f (А,В,С,Д)=АВ+ВСД+ВС+АВД