Формы записи булевых функций.

Табличная запись.

Одним из распространенных способов записи булевой функции является ее задание с помощью таблицы соответствия (таблицы истинности), которая сопоставляет всем двоичным наборам аргументов значения функции на этих наборах. Буквы и наборы в таблице могут располагаться в любом порядке, однако практически целесообразно осуществлять запись следующим образом:

1) порядок записи букв в таблице совпадает с порядком аргументов в записи функции;

2) наборы, представляющие собой двоичные числа, располагаются в таблице в порядке их возрастания. Каждому набору приписывается номер соответственно представляемому им числу:

000…00 – нулевой набор;

000 …01 – 1-й набор;

. . . . . . . . . . . . . . . . . . .

111 … 11 - (2ⁿ-1)–й набор.

Функция, записанная в табличном виде, имеет индекс, равный двоичному числу, образованному значениями этой функции, записанными слева направо, начиная со значения на нулевом наборе.

Пример. Запись функции f₂₄₈(АВС) = 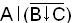приведена в табл.1.5

Таблица 1.5

A B C B↓C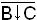

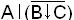
0 0 0 1 0 1

0 0 1 0 1 1

0 1 0 0 1 1

0 1 1 0 1 1

1 0 0 1 0 1

1 0 1 0 1 0

1 1 0 0 1 0

1 1 1 0 1 0

При задании булевых функций при 3≤n≤10 иногда используют прямоугольные таблицы, т.е. те же таблицы соответствия, но в несколько ином начертании, позволяющем получить более компактную запись. Для функции от n переменных такая таблица имеет 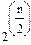строк и 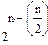столбцов, где 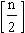- целая часть числа n/2.

Пример. Запись функции f(ABCD)=[(C→D)~B] 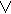[A |0] дана в табл.1.6

Пример. Запись функции f(ABCD)= 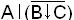приведена в табл.1.7

Таблица 1.6 Таблица 1.7

CD BC

А

AB 00 01 10 11 00 01 10 11

00 1 1 1 1 0 1 1 1 1

01 1 1 1 1 1 1 0 0 0

10 0 0 1 0

11 1 1 0 1

Аналитическая запись.

Произведение булевых переменных называется булевым произведением. Булево произведение называется элементарным, если переменные в него входят только один раз в прямой или инверсной форме.

Пример. 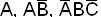- элементарные произведения, 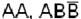- эти произведения не являются элементарными.

Число переменных, образующих элементарное произведение, называется длиной или рангом элементарного произведения.

Пример. 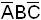- ранг 3.

Минтермом или конституентой единицы n переменных называется элементарное произведение ранга n.

Аналогичные определения существует и для булевых сумм.

Пример. 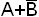- элементарная сумма ранга 2; 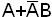не является элементарной суммой.

Макстермом или конституентой нуля n переменных называется элементарная булева сумма ранга n.

Как булева функция минтерм принимает значение единицы только на одном наборе, аналогично макстерм принимает только на одном наборе значение нуля.

При записи минтерма часто используется буква m с индексом того набора, на котором данный минтерм принимает значение единицы.

Пример. 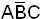=m₅.

Двоичный эквивалент индекса для минтерма может быть определен из записи минтерма подстановкой вместо прямых форм переменных цифры 1, а вместо инверсных – цифры 0.

Пример. 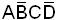- минтерм ранга 4;

1010 – двоичный эквивалент индекса.

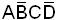= m₁₀.

При этом не следует забывать, что при переходе от индексной записи минтерма к аналитической следует восстановить все переменные, входящие в данную запись.

Пример. m₅ – ранга 4 имеет запись 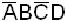; m₅ – ранга 3 имеет запись .

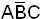Аналогично при записи макстерма используется буква М с индексом, двоичная запись которого содержит 1, если соответствующая переменная входит в аналитическую запись макстерма в прямой форме, и 0, если в инверсной.

Пример. 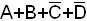=М₁₁₀₀= М₁₂.

Между минтермами и макстермами существует следующая связь:

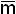_i = M₂ⁿ_-i-1; 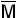_i = m₂ⁿ_-i-1.

Булева сумма всех минтермов ранга n равна единице:

2ⁿ-1

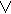m_i =1.

i=0

Это следует из того, что число различных минтермов ранга n равно 2ⁿ, т.е. числу различных наборов n переменных, а функция, принимающая на всех наборах значение 1, есть константа 1.

Используя теорему де Моргана, можно показать, что произведение всех макстермов ранга n равно нулю:

2ⁿ-1

Λ M_i =0.

i=0

Из этих уравнений следует

m_im_j =0 при i≠j;

M_i + M_j =1 при i≠j.

Равенства очевидны, если вспомнить, что минтерм – это конституента единицы, а макстерм – конституента нуля.

Основная теорема.

Любая булева функция может быть выражена булевой суммой минтермов или произведением макстермов.

Таблица 1.8 Составим таблицу функций и найдем булево

A B C f(ABC) выражение для данной функции. Из табл.1.8 видно,

0 0 0 0= α₀ что функция равна единице, только на наборах,

0 0 1 1= α₁ равных 001, 101, 111, что соответствует минтер-

0 1 0 0= α₂ мам .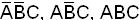

0 1 1 0= α₃ Это значит, что данная функция может быть

1 0 0 0= α₄ дизъюнкцией этих минтермов, т.е.

1 0 1 1= α₅ 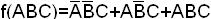= m₁ + m₅+ m₇.

1 1 0 0= α₆ Чтобы убедиться в сказанном, запишем дан-

1 1 1 1= α₇ ную функцию в виде суммы произведений значений функции на соответствующие минтермы:

f(ABC)= α₀ m₀ + α₁ m₁ + α₂ m₂ + α₃ m₃ + α₄ m₄ + α₅ m₅ + α₆ m₆ + α₇ m₇ =

= 0m₀ + 1m₁ + 0m₂ + 0m₃ + 0m₄ + 1m₅ + 0m₆ + 1m₇ ,

где α_i – значение данной функции на i –ом наборе.

Следовательно, справедлива запись:

2ⁿ-1

f(x₁ x₂ … x_n)= 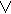α _i m_i .

i=0

Применив формулу де Моргана, найдем выражение

2ⁿ-1

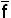( x₁ x₂ … x_n)=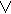 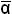_i m_i .

i=0

2ⁿ-1 2ⁿ-1 2ⁿ-1 2ⁿ-1

f(x₁ x₂ … x_n)= 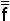(x₁ x₂ … x_n)=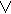 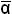_i m_i = Λ ( 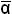_i m_i)= Λ (α _i + 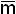_i)= Λ (α _i +M₂ⁿ_-i-1).

i=0 i=0 i=0 i=0

Основная теорема:

2ⁿ-1 2ⁿ-1

f(x₁ x₂ … x_n)= 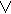α _i m_i = Λ (α _i +M₂ⁿ_-i-1).

i=0 i=0

Для аналитических записей булевых функций существуют следующие определения:

Булева сумма элементарных произведений называется дизъюнктивной нормальной формой (ДНФ).

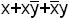- ДНФ;

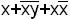- не является ДНФ.

Булево произведение элементарных сумм называется конъюнктивной нормальной формой (КНФ).

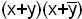- КНФ;

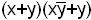-не является КНФ.

ДНФ функции n переменных, состоящая из элементарных произведений ранга n (т.е. из минтермов), называется совершенной дизъюнктивной нормальной формой функции (СДНФ).

КНФ функции n переменных, состоящая из элементарных сумм ранга n (т.е. из макстермов), называется совершенной конъюнктивной нормальной формой функции (СКНФ).

Основная теорема содержит запись СДНФ и СКНФ функций.

Из теоремы следует, что запись СДНФ (или СКНФ) булевой функции единственна.

Выражение функции в СДНФ и СКНФ с помощью аналитических преобразований.

Для получения СДНФ функции аналитическим способом используется следующий прием:

1) аналитическое выражение функции приводится к бесскобочной записи в форме дизъюнкции каких-либо конъюнкций;

2) каждая конъюнкция, имеющая число сомножителей меньше n, умножается на выражение «1» через все недостающие переменные ( );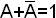

3) раскрываются скобки и приводятся подобные члены.

Пример. Найти СДНФ функции f(ABCD)= .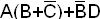

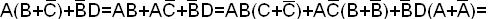
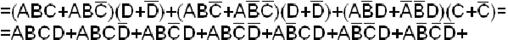
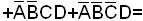m₁₅ + m₁₄ + m₁₃ + m₁₂ + m₁₁ + m₉ + m₈ + m₃ +m₁.

Для получения СКНФ функции без использования табличной записи следует применять процедуру вида:

1) аналитическое выражение функции приводится с помощью соотношения AB+C=(A+C)(B+C) к конъюнктивной записи со скобками, причем в скобках должны стоять дизъюнкции отдельных переменных в прямой или инверсной форме;

2) к каждой дизъюнкции добавляется выражение 0 через все недостающие переменные ( );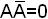

3) вновь используется дистрибутивный закон вида и приводятся подобные члены.

Пример. Найти СКНФ функции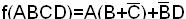

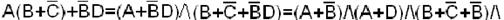
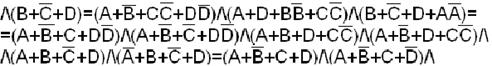
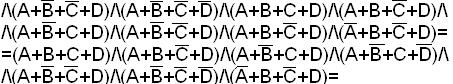
=М₁₅ М₁₃ М₁₁ М₁₀ М₉ М₈ М₅

Рассмотрим расширение сокращенной записи элементарного произведения до суммы минтермов.

Пусть 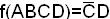, представим данную запись в виде

A B C D

- - 0 1

Затем, не меняя значений известных цифр в записи индекса минтерма, подставляем все возможные комбинации цифр соответствующих разрядов:

0 0 0 1

0 1 0 1

1 0 0 1

1 1 0 1

Полученные цифры соответствуют индексам минтермов, содержащихся в СДНФ исходной функции, т.е.

f(ABCD)=m₁+m₅+m₉+m_13.