Анализ участка схемы с параллельным соединением

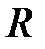и - элементов

Рассмотрим анализ ещё одной простейшей цепи (рис. 18), содержащей параллельное соединение R и C-элементов. Данной схемой замещения на достаточно низкой частоте можно представить некоторые типы конденсаторов, если помимо его основного свойства – накапливать заряды, необходимо учесть сопротивление утечки зарядов из-за несовершенства диэлектрика, разделяющего обкладки конденсатора. Допустим, конденсатор подключён к синусоидальному напряжению

.

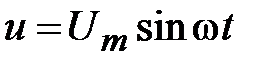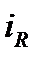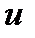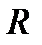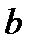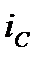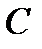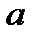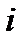Рис. 18.

Зададим (произвольно) положительное направление токов в ветвях для узла и составим уравнение по 1-ому закону Кирхгофа:

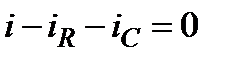.(80)

Учитывая, что R-элемент и С-элемент соединены параллельно, получим из (29) и (52):

.

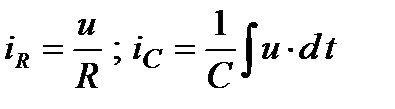Тогда уравнение (80) примет вид

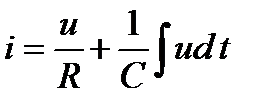.(81)

Для нахождения i(t) необходимо решить интегральное равнение. Для упрощения анализа перейдём к комплексной форме записи напряжений и токов. Согласно соотношений (33) и (59):

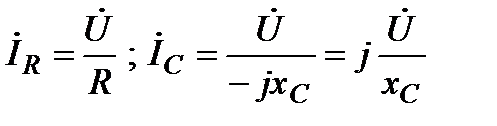, (82)

где 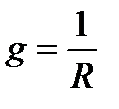– проводимость R-элемента; 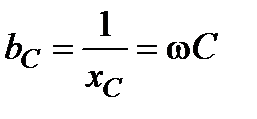– проводимость ёмкостного элемента. Эти параметры измеряются в сименсах (См). В комплексной форме записи уравнение (80) будет иметь вид:

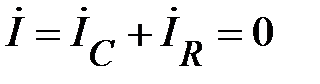. (83)

Подставим (82) в (83) получим:

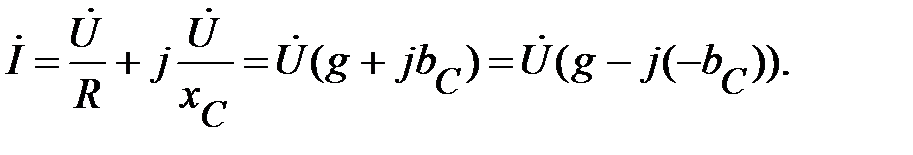(84)

Уравнение (84) представляет собой закон Ома для данной цепи. Комплексное число

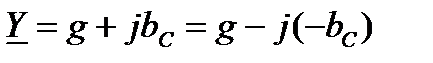(85)

называется полной комплексной проводимостью данного участка цепи и измеряется (условно) в Сименсах (См). Эту величину можно изобразить на комплексной плоскости.

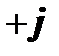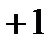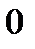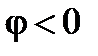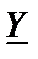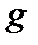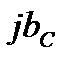Рис. 19.

Действительная часть комплексной проводимости:

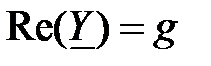
называется активной составляющей полной комплексной проводимости. Мнимая часть комплексной проводимости:

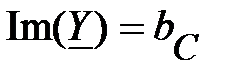
называется модулем реактивной составляющей полной комплексной проводимости или модулем реактивной проводимости участка цепи (для данной схемы эта величина также является модулем комплексной проводимости - элемента). Треугольник, представленный 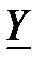и её составляющими (рис. 19), называется треугольником проводимостей. Соотношение (85) представляет алгебраическую форму записи комплекса Y для данной цепи. В расчётах также получила распространение показательная форма записи Y:

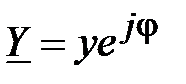, (86)

где 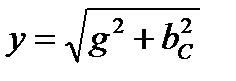– полная проводимость данного участка цепи, измеряется в Сименсах (См); φ – фазовый угол полной проводимости измеряется в угловых градусах или радианах

,

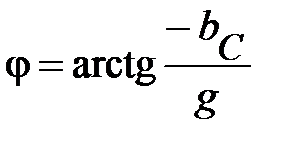причем 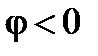(как показывает рис. 19). Из треугольника проводимостей становятся очевидными следующие соотношения

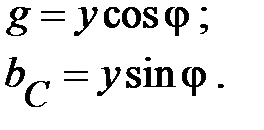(87)

Согласно соотношениям (82) будем иметь

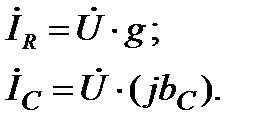(88)

Откуда

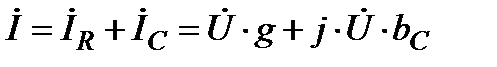. (89)

Отразим соотношение (89) на векторной диаграмме. Построение начинаем с заданного вектора 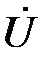. Задаёмся масштабами m_u (В/см) и m_i (А/см). Т.к. по условию ψ_u = 0, то вектор 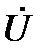будет расположен вдоль оси +1(рис. 20).

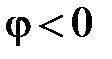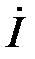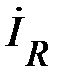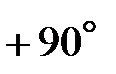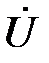K

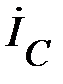N

Рис. 20.

В положительном направление оси абсцисс от точки 0 откладываем отрезок длиной, равной 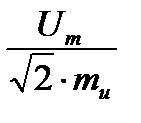(см). Конец отрезка отмечаем стрелкой. Вектор 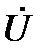построен. Далее строим вектор 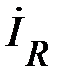. Как показано на рис. 6, 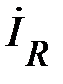должен совпадать по направлению с вектором 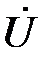. Поэтому от точки 0 в положительном направлении оси абсцисс откладываем отрезок длиной, равной 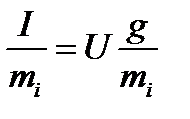(см). Его конец отмечаем стрелкой. Вектор 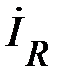построен. Для построения вектора 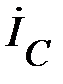учтём, что в соответствии с ранее установленным (54), вектор тока через С-элемент 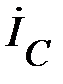должен опережать вектор напряжения на С-элементе 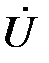на 90º. В соответствии с этим условием вектор 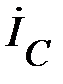должен лежать на луче KN. Направление, которого получено его поворотом от оси +1 на 90º в положительном направлении. Т. е. из конца вектора 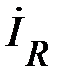(т. К) восстанавливаем перпендикуляр KN к оси +1. На этом перпендикуляре откладываем отрезок, равный 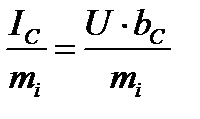(см). Конец отмечаем стрелкой. Вектор 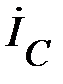построен. В соответствии с правилом суммирования векторов вектор, соединяющий т. 0 и конец вектора 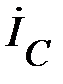, равен 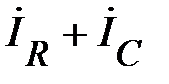. Согласно (89) это будет вектор полного тока в цепи

.

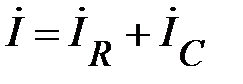Т. о., данная векторная диаграмма даёт геометрическую интерпретациюпервого закона Кирхгофа для узла 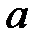в данной цепи (рис.18). Прямоугольный треугольник (рис. 20) называется треугольником токов. Из него следуют соотношения, связывающие модули токов в цепи

;

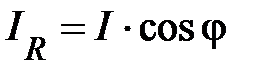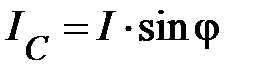. (90)

В заключение рассмотрим энергетические соотношения на этом участке цепи. Поскольку в данной цепи (рис.18) включены R-элемент и С-элемент, то интенсивность энергетических процессов характеризуется совокупностью активной и реактивной мощностей. При этом полная мощность определится

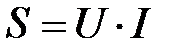; (91)

активная мощность

;

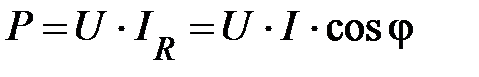реактивная мощность

.

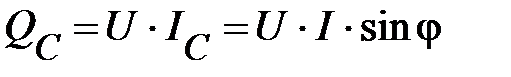Полная мощность и её составляющие связаны соотношением

.

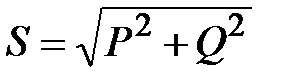В комплексной форме эта связь имеет вид

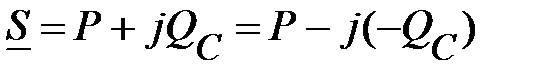. (92)

Соотношение (92) можно отразить на комплексной плоскости в виде треугольника мощностей (рис.21).

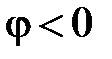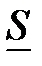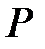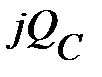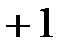Рис. 21

Отметим, что треугольники проводимостей (рис.19), токов (рис. 20) и мощностей (рис. 21) подобны, т. е.

.

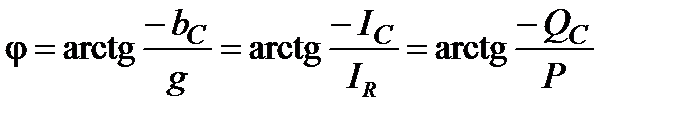Студентам предлагается самостоятельно провести анализ участка цепи с параллельным соединением R- и L-элементов.

ЛИТЕРАТУРА

1. Касаткин А.С., Немцов М.В. Электротехника: Учеб. для вузов. М.: Издательский центр «Академия». 2003.

2. Электротехника и электроника. В 3 кн. / Под ред. В.Г. Герасимова. М.: Энергоатомиздат, 1996.

3. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. В 3 т. Л.: Энергия, 1981.

ЛАБОРАТОРНАЯ РАБОТА № 5