Участок цепи с индуктивным элементом

Индуктивным или 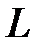-элементом называют такой идеализированный элемент схемы замещения, который способен лишь преобразовывать электрическую энергию, и накапливать её в виде энергии собственного магнитного поля, а также при определённых условиях осуществлять обратное преобразование, отдавая всю накопленную энергию без остатка во внешнюю цепь.

Реальным прообразом этой модели может служить катушка индуктивности. Однако провод, из которого выполняется катушка индуктивности, обладает сопротивлением на постоянном токе. Кроме того, катушка индуктивности обладает и другими свойствами на переменном токе, которые не являются основными свойствами и в данной модели не учитываются.

Из курса физики известно, что изменяющийся во времени ток создаёт в окружающем катушку пространстве переменное магнитное поле, которое может быть охарактеризовано в целом величиной, называемой потокосцеплением 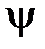. Потокосцепление определяется как

,

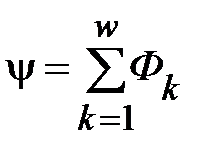где 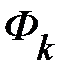– магнитный поток, пронизывающий контур, ограниченный 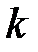-тым витком катушки, а 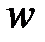– число витков катушки. Потокосцепление 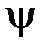, как и магнитный поток 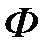, измеряются в веберах (Вб). Переменный магнитный поток, пронизывая витки катушки, индуцирует в катушке ЭДС самоиндукции :

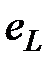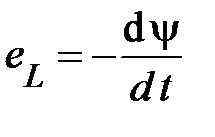(Закон электромагнитной индукции Фарадея – Ленца) (37)

Связь между током в катушке и её потокосцеплением определяется соотношением

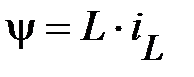, (38)

где 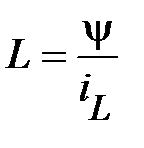– является количественным параметром, характеризующим способность катушки запасать энергию магнитного поля. Этот параметр называется индуктивностью и измеряется в Генри (Гн). В соответствии с (37) и (38) если 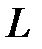-постоянная величина, то

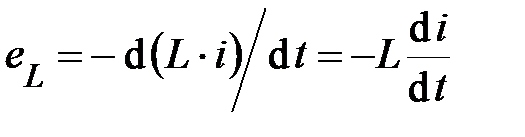(39)

Все рассмотренные зависимости и явления, происходящие в катушке индуктивности, справедливы и для её идеализированной модели – индуктивного элемента. При протекании через него переменного тока на его концах возникает разность потенциалов, которая в любой момент времени уравновешивает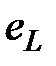

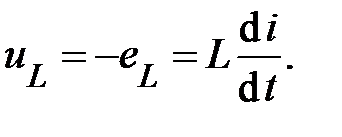(40)

Согласно определению 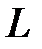-элемент безвозвратно электрическую энергию не потребляет (например, не рассеивает в виде тепла). Он лишь преобразует её и запасает в виде энергии собственного магнитного поля. Однако можно ввести понятие о мощности индуктивного элемента, понимая под этим скорость преобразования энергии электрического тока в энергию магнитного поля. Т.е. мгновенную мощность 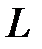-элемента можно определить:

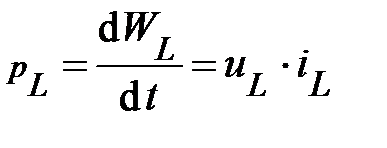. (41)

Энергия магнитного поля 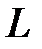-элемента, накопленная к рассматриваемому моменту времени 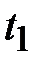определится, с учётом (40)

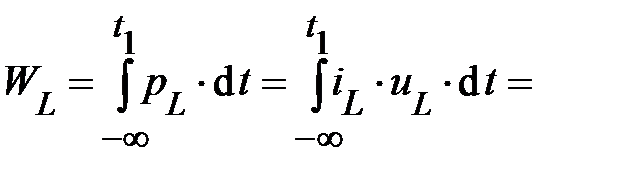
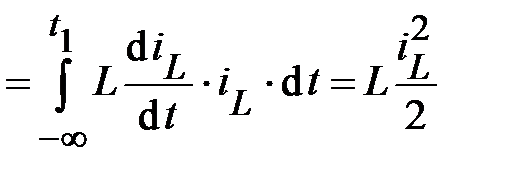. (42)

Пусть через индуктивный элемент протекает синусоидальный ток (рис. 8) .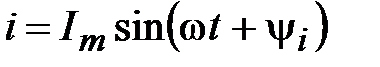

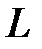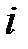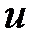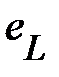Рис. 8.

В этом случае потокосцепление 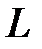-элемента

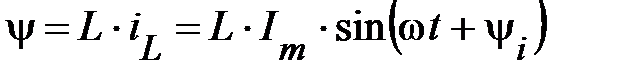
Согласно (39) и (40)

.

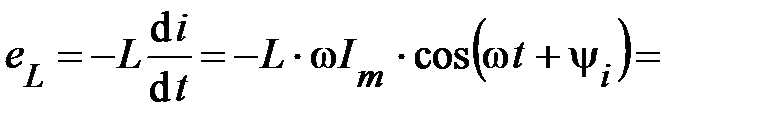
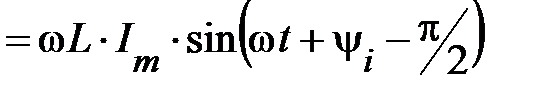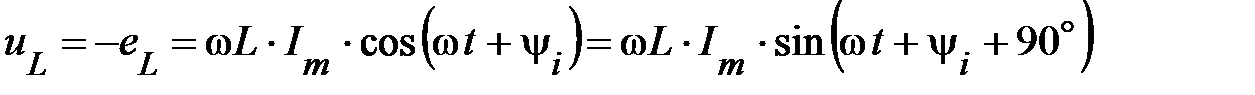. (43)

Т.о., при синусоидальном токе напряжение на 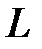-элементе также синусоидально: напряжение и ток изменяются с одинаковой частотой; напряжение опережает ток по фазе на четверть периода: 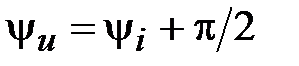. Угол сдвига фаз 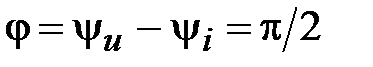. Волновые диаграммы 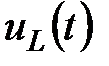и 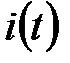приведены на рис. 9.

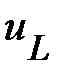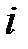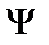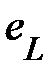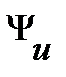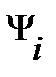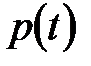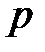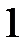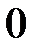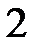Рис. 9.

Из соотношения (44) имеем:

.

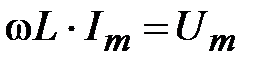Это есть закон Ома для амплитудных значений напряжения и тока. Для действующих значений этих величин закон Ома будет иметь вид:

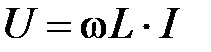. (44)

Величину 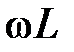, имеющую размерность Ом, обозначают 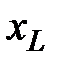и называют индуктивным сопротивлением 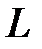-элемента. С учетом этого получим

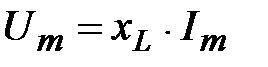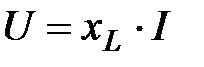; (45)

Построим комплексную форму записи закона Ома на этом элементе. Для этого перейдем от 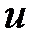и 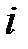как синусоидальных функций времени к однозначно изображающим их комплексам действующих значений напряжения и тока

;

.

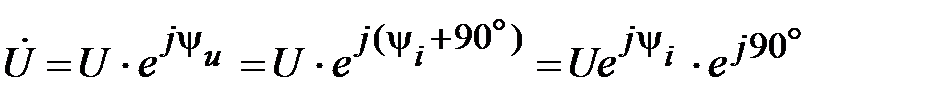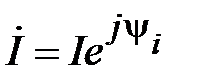Возьмем формальное отношение

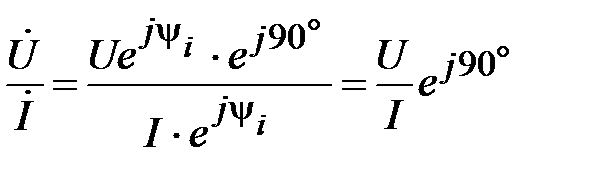. (46)

Но из (45) следует

,

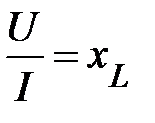а из (19) получим

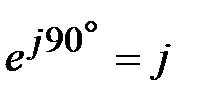
и окончательно

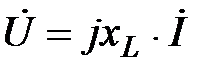. (47)

Это закон Ома в комплексной форме для участка цепи с 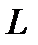-элементом. Величина 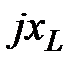называется комплексным сопротивлением индуктивного элемента. Оно является положительным мнимым числом, модуль которого равен .

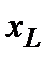Векторная диаграмма для индуктивного элемента построена по соотношениям (43), (46) на рис.10. На ней вектор напряжения на индуктивном элементе опережает вектор тока на угол 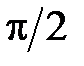. Векторы 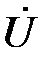и 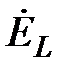находятся в противофазе, вектор потокосцепления 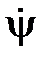находится в фазе с током .

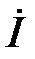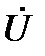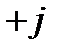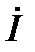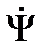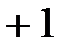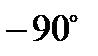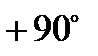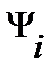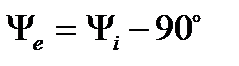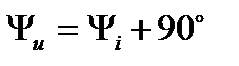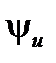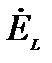Рис. 10.

Рассмотрим энергетические процессы на участке цепи с 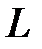-элементом. Мгновенная мощность индуктивного элемента:

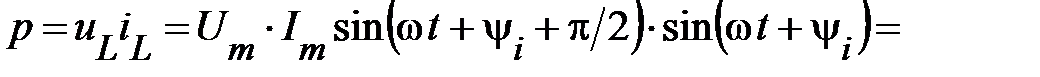
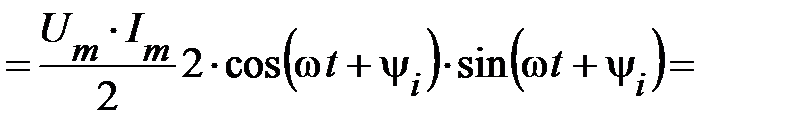
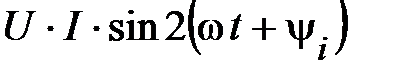. (48)

Т.е. мгновенная мощность в цепи с 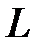-элементом колеблется с частотой 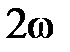и амплитудой 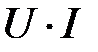вокруг нулевого положения (рис.9).Поэтому среднее значение мощности за период равно нулю. Это ещё раз показывает, что 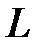-элемент безвозвратно электрическую энергию потребляет. Рассмотрим на волновой диаграмме (рис.9) процесс обмена энергией между 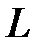-элементом и источником питания. В течение первой четверти периода изменение 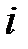(отрезок времени между точками 1 – 3 на рис.9) ток 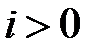и напряжение 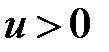, и напряжение ui >0, поэтому на этом участке 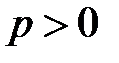, т.е. 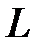-элемент работает в режиме потребителя (нагрузки): электрическая энергия, поступающая от источника питания к элементу преобразуется в энергию магнитного поля и накапливается 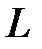-элементом (заштрихованная область под кривой на рис.9). В течение второй четверти периода (отрезок времени между точками 3 – 5) ток 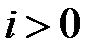, а напряжение 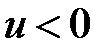, поэтому 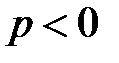, т.е. 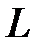-элемент работает в режиме источника энергии. В этот промежуток времени происходит процесс обратного преобразования энергии магнитного поля в электрическую энергию, которая возвращается во внешнюю цепь. В момент времени, определяемый точкой 5 на рис.9 весь запас энергии возвращается L-элементом. Далее процесс повторяется при отрицательных значениях тока.

Т.о. в цепи с 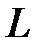-элементом не совершается работа, а происходит периодический обмен энергией между источником и магнитным полем с частотой 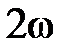. Интенсивность этого обмена принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле, т.е. амплитудным значением мгновенной мощности, которое называют реактивной мощностью и обозначают 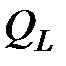. Как следует из (42)

.

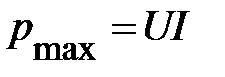С учетом (45) получим

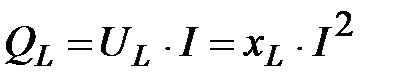. (49)

Единице реактивной мощности присвоено название вольтампер реактивный, сокращённо ВАр.