Распределение надежности из условия сохранения относительной уязвимости

Элементов.

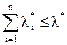При использовании метода предполагается, что подсистемы соединены последовательно и имеют постоянную интенсивность отказов, что отказ любой подсистемы вызывает отказ всей системы и что заданная наработка подсистем равна заданной наработке системы. При использовании этого метода необходимо выразить требуемую надежность через интенсивности отказов. Задача состоит в том, чтобы выбрать такие λ^*_i, что

где λ^*_i – заданная интенсивность отказов i-ой подсистемы, а λ^*– требуемая интенсивность отказов системы.

Метод включает следующие этапы:

1. Определение интенсивности отказов подсистем λ_i по результатам наблюдений или на основе оценок по данным за прошлое время.

2. Задание весового множителя ω_i для каждой подсистемы в соответствии с интенсивностями отказов, определенными на этапе 1; ω_i определяется по формуле

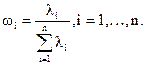3. Вычисление требуемой интенсивности отказов подсистемы с помощью соотношения

λ^*_i = ω_iλ^* , i = 1, …, n.

Ясно, что этот метод позволяет задать новые значения интенсивности отказов на основе весовых множителей, которые являются функциями интенсивностей отказов подсистем за прошлое время.

Нормирование надежности при структурном резервировании

элементов системы.

При использовании уже существующих элементов, задача обеспечения заданных уровней надежности системы может быть решена использованием структурного резервирования.

При решении поставленной задачи примем, что вероятность безотказной работы нерезервированного i-ого элемента 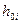за период T_r оценивается по произвольному закону распределения F(x) h _0i = 1 – F(T_r)

Соответственно вероятность отказа i-ого нерезервированного элемента будет равна

q_0i = 1 – h_0i.

При структурном резервировании вероятность отказа i-го элемента 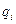, может быть замещением отказавшего элемента («холодный» резерв)

,

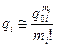где 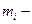общее число элементов в резервной группе ( кратность резерва ).

Производя логарифмирование, получим

.

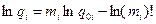В дальнейшем соотношение представим в виде

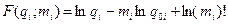
Затраты на производство и эксплуатацию i-ого элемента системы будут равны

С_Эi = C_0im_i,

где С_Эi – стоимость i-ой системы.

Полученные результаты позволяют перейти к решению задачи нормирования надежности элементов, то-есть оптимального распределения уровней надежности между отдельными элементами системы, обеспечивающих удовлетворение заданных требований к надежности системы в целом при минимальном расходе средств на реализацию целевой программы. Очевидно, затраты на производство и эксплуатацию системы, состоящей из n элементов, будут равны

.

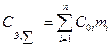Соответственно надежность системы, состоящей из n

последовательно соединенных элементов, будет равна

.

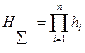Для высоконадежных систем вероятность отказа можно оценить по приближенному соотношению

,

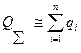где q_i = 1 – h_i.

Очевидно заданные требования к надежности системы могут быть обеспечены при различных комбинациях значений слагаемых q_i. Среди множества значений q_i целесообразно выбрать такие, которые обеспечивают минимум затрат на реализацию целевой программы. Поставленную задачу будем решать методом Лагранжа.

В рассматриваемом случае функция Лагранжа примет вид

,

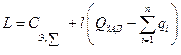где l – множитель Лагранжа.

При этом оптимальные уровни q_i, должны удовлетворять условию .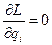

Раскрывая выражение производной, получим ,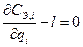

Производная от затрат по q_i оценивается по соотношению

,

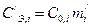где .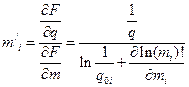

Для нахождения производной воспользуемся приближенной оценкой функционала m!.

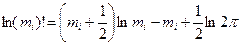
Предполагая, что дискретная функция 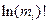может быть аппроксимирована непрерывной зависимостью, проведем формальное дифференцирование

.

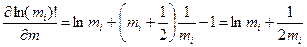Таким образом, окончательно получим

,

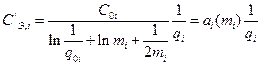где .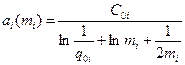

После подстановки 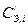в условие оптимальности найдем .

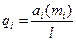С учетом выражения для 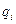дисциплинирующее условие примет вид

. .

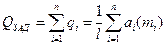Разрешая это соотношение относительно неопределенного множителя Лагранжа , найдем

.

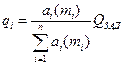Окончательный результат можно получить методом последовательных приближений. В качестве нулевого приближения можно принять равномерное распределение надежности

.

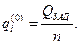Значение 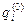позволяет найти оценку 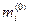из соотношения .

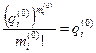Итерационный процесс заканчивается по достижении требуемой точности вычислений.

В случае «горячего» резерва, при проведении расчетов, следует принять

.

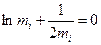Отсюда .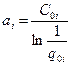

При этом кратность резерва рассчитывается по соотношению

,

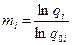где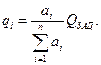

Лекция № 7