Решение задач синтеза линейных систем

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ, КОРРЕКЦИЯ

ИХ ДИНАМИЧЕСКИХ СВОЙСТВ

6.1. Назначение и виды коррекции динамических свойств

систем автоматического управления

Задача синтеза систем автоматического управления (коррекция их динамических свойств) состоит в выборе структуры и параметров систем регулирования объектами, которые в соответствии с заданными техническими условиями обеспечивают наиболее рациональные характеристики по запасам устойчивости и показателям качества.

Коррекция осуществляется с помощью введения в систему специальных корректирующих звеньев с особо подобранной передаточной функцией.

Таким образом, задача синтеза включает в себя определение структуры и параметров корректирующих звеньев при известных параметрах остальных звеньев, входящих в систему, с учетом заданных технических условий.

Корректирующие звенья по способу включения можно разделить (рис.6.1):

1) на последовательные (рис.6.1, а);

2) параллельные (рис.6.1, б);

3) стоящие в обратной связи (местные или главная обратные связи) (рис.6.1, в).

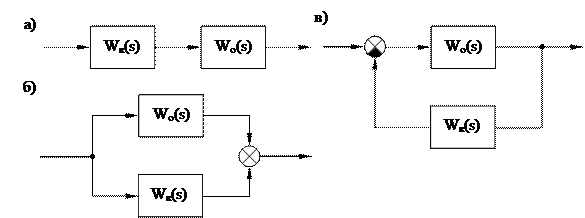Рис.6.1. Способы включения корректирующих звеньев в систему:

W_о(s) – передаточная функция основных звеньев системы;

W_к(s) – передаточная функция корректирующего звена

Действие корректирующих звеньев сводится к следующему:

1) введение в контур САУ пропорциональных воздействий либо
воздействий по производным и/или интегралам (дифференцирующие и/или интегрирующие звенья);

2) введение корректирующих воздействий параллельно отдельным звеньям;

3) введение корректирующих обратных связей вокруг отдельных частей системы либо в главную обратную связь системы;

4) введение корректирующих воздействий в функции внешних воздействий и их производных (управление по возмущению).

В непрерывных системах автоматического управления используется множество типов корректирующих устройств и в общем случае их структура может быть любой. Однако в теории автоматического управления выделяют типовые корректирующие звенья, которые называются регуляторами.

По принципу действия регуляторы классифицируют следующим образом:

Пропорциональные (П), имеющие передаточную функцию:

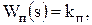(6.1)

где k_п – коэффициент усиления пропорционального регулятора.

Пропорционально-дифференцирующие (ПД):

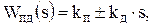(6.2)

где k_п – коэффициент усиления пропорциональной составляющей регулятора; k_д – коэффициент усиления дифференцирующей составляющей регулятора.

Пропорционально-интегрирующие (ПИ):

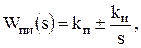(6.3)

где k_п – коэффициент усиления пропорциональной составляющей регулятора; k_и – коэффициент усиления интегрирующей составляющей регулятора.

Пропорционально-интегродифференцирующие (ПИД):

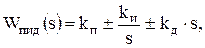(6.4)

где k_п – коэффициент усиления пропорциональной составляющей регулятора; k_и – коэффициент усиления интегрирующей составляющей регулятора; k_д – коэффициент усиления дифференцирующей составляющей регулятора.

Приведенные выше типовые регуляторы являются идеальными, то есть не учитывающими инерционность составляющих регулятора.

С учетом инерционности регуляторов (реальные регуляторы):

Пропорциональные (П):

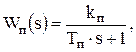(6.5)

где T_п – постоянная времени пропорционального регулятора.

Пропорционально-дифференцирующие (ПД):

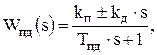(6.6)

где T_пд – постоянная времени пропорционально-дифференцирующего регулятора.

Пропорционально-интегрирующие (ПИ):

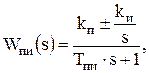(6.7)

где T_пи – постоянная времени пропорционально-интегрирующего регулятора.

Пропорционально-интегродифференцирующие (ПИД):

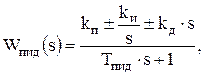(6.8)

где T_пид – постоянная времени пропорционально-интегро-дифференцирующего регулятора.

Применение идеальных регуляторов в реальных САУ возможно, если постоянная времени применяемого регулятора достаточно мала и можно принять, что она равна нулю, в этом случае все реальные регуляторы превращаются в идеальные.

Корректирующие обратные связи делятся:

− По знаку обратной связи:

а) на отрицательные;

б) положительные.