Основные критерии гидродинамического и теплового подобия
Теория, изучающая условия подобия различных объектов (физических явлений, процессов, аппаратов, систем), отличающихся масштабами, геометрией или физической природой, называется теорией подобия. Основные задачи теории подобия: установление критериев подобия разных объектов, изучение их свойств с помощью этих критериев, определение возможности обобщения результатов решения конкретных задач при отсутствии способов нахождения их полных решений. Два объекта подобны, если в соответствующие (сходственные) моменты времени в соответствующих точках пространства значения переменных величин, характеризующих состояние одного объекта, пропорциональны значениям соответствующих величин др. объекта. Коэффициент пропорциональности соответствующих величин называются коэффициентами подобия.
Основной метод теории подобия - анализ размерностей физических величин, характеризующих состояние объекта исследования, и параметров, которые определяют это состояние. Базой анализа размерностей служит требование, согласно которому основные уравнения, выражающие связь между переменными и параметрами объекта, должны быть справедливы при любом выборе единиц измерения входящих в них величин; значения переменных определяются решением данной системы уравнений, значения параметров должны быть заданы для решения этой системы. Из этого требования следует, в общем, что все слагаемые - каждого уравнения должны иметь одинаковые размерности и, в частности, что с помощью операции, наз. нормализацией (преобразованием), могут быть приведены к безразмерному виду.
Эти уравнения содержат, как правило, величины двух типов: а) безразмерные зависимые и независимые переменные; б) безразмерные параметры (иногда называют комплексами). Последние включают характерные размеры (масштабы) объекта, а также физические параметры исходного уравнения и граничных условий. Объекты, описание свойств которых сводится к одинаковым безразмерным уравнениям и граничным условиям, независимо от их физической природы относятся к одному классу. Очевидно, что геометрически подобные или даже физически идентичные системы нельзя относить к одному классу, если граничные условия для них не будут представлены одинаково (например, при различных профилях скоростей потока на входе в идентичные аппараты).
Объекты, относящиеся к одному классу и имеющие одинаковые численные значения комплексов в уравнениях и соответствующих граничных условиях, подобны, поскольку поля изменения физ. характеристик, определяемые безразмерными переменными, отличаются лишь выбранными масштабными коэффициентами, отношения которых задают коэффициенты подобия. Поэтому комплексы называют также критериями или числами подобия, равенство которых для объектов, описываемых идентичными безразмерными уравнениями и граничными условиями, обеспечивает их подобие.
Таким образом, можно, не решая уравнений, объединить физические величины в безразмерные комплексы и получить вид безразмерных (критериальных) уравнений с меньшим числом переменных. Решение этих уравнений позволяет находить искомые величины. Точные критериальные уравнения описываются путем проведения соответствующих экспериментов.
Выше рассматривалось, что 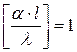 - безразмерный комплекс. Этот комплекс называется критерием Нуссельта
- безразмерный комплекс. Этот комплекс называется критерием Нуссельта  . Внешне критерий Нуссельта имеет вид, аналогичный критерию Био
. Внешне критерий Нуссельта имеет вид, аналогичный критерию Био 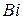 . Разница заключается в том, что
. Разница заключается в том, что 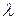 в первом случае берется для газов, а во втором – для обтекаемого тела. Объединение характерных величин в безразмерные критерии позволяет определить количественные соотношения множества явлений. Размерное уравнение
в первом случае берется для газов, а во втором – для обтекаемого тела. Объединение характерных величин в безразмерные критерии позволяет определить количественные соотношения множества явлений. Размерное уравнение 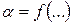 при вынужденном движении в трубах может быть приведено к безразмерному виду:
при вынужденном движении в трубах может быть приведено к безразмерному виду:
 .
.
Полученные опытным путем уравнения имеют вид:
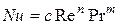 ,
,
где  - постоянная величина,
- постоянная величина, 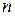 и
и 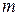 - показатели степени.
- показатели степени. 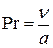 - критерий Прандтля (физических свойств среды);
- критерий Прандтля (физических свойств среды);
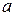 - коэффициент температуропроводности. В теплотехнике встречаются и другие критерии подобия.
- коэффициент температуропроводности. В теплотехнике встречаются и другие критерии подобия.
Таблица 12.1 - Главные безразмерные критерии тепловых и гидродинамических процессов
| Название, формула | Величины, входящие в критерий | Значение критерия |
1. Критерий Рейнольдса (критерий режима движения) 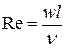 | 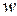 - скорость, м/с; - скорость, м/с; 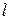 - характерный размер, м; - характерный размер, м; 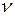 - коэффициент кинематической вязкости, м2/с. - коэффициент кинематической вязкости, м2/с. | Мера соотношения сил инерции и вязкости; определяет гидродинамический режим движения |
2. Критерий Эйлера (критерий падения давления)  |  -перепад давления, Па; -перепад давления, Па; 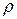 - плотность жидкости, кг/м3. - плотность жидкости, кг/м3. | Мера соотношения между изменением силы гидростатического давления и силой инерции; отражает влияние перепада давления на движение потока |
3. Критерий Прандтля 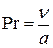 | 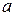 - коэффициент температуропроводности, м2/с - коэффициент температуропроводности, м2/с | Характеризует физические свойства жидкости. Мера соотношения вязкостных и температуропроводных свойств теплоносителя; мера соотношения полей скоростей и температур в потоке |
4. Критерий Пекле  | см.выше | Мера отношения молекулярного и конвективного переноса тепла в потоке |
5. Критерий Нуссельта (критерий теплоотдачи)  | 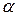 - коэффициент конвективной теплоотдачи, Вт/(м2К); - коэффициент конвективной теплоотдачи, Вт/(м2К); 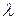 - коэффициент теплопроводности теплоносителя, Вт/(м·К) - коэффициент теплопроводности теплоносителя, Вт/(м·К) | Характеризует отношение между интенсивностью теплоотдачи и температурным полем в пограничном слое потока |
6. Критерий Био 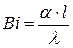 | 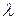 - коэффициент теплопроводности твердого тела, Вт/(м·К) - коэффициент теплопроводности твердого тела, Вт/(м·К) | Мера соотношения между внутренними и внешними термическими сопротивлениями |
Продолжение таблицы 12.1
7. Критерий Фурье (безразмерное время)  | 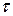 - время (сек) - время (сек) | Характеризует связь между скоростью изменения температурного поля, физическими константами и размерами тела. |
8. Критерий Грасгофа  | 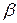 - коэффициент объемного расширения, К-1; - коэффициент объемного расширения, К-1;  -ускорение свободного падения, м/с2; -ускорение свободного падения, м/с2; 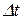 -температурный напор между теплоносителем и теплопередающей поверхностью, К -температурный напор между теплоносителем и теплопередающей поверхностью, К | Определяет соотношение подъемной силы, вызываемой разностью плотностей холодных и нагретых частиц жидкости и сил молекулярного трения (интенсивность свободного движения жидкости) |
9. Критерий Архимеда 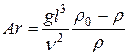 | 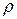 и и 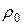 - плотности одной и другой фазы - плотности одной и другой фазы | Используют при рассмотрении движения жидкости, в которой имеется взвесь твердых частиц или пузырьков. При  идентичен идентичен 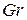 |
Любая комбинация основных критериев подобия может служить критерием подобия.
Литература: [4], с. 47-52; [5], с. 162-165; [11], с. 35-39; [12], с. 39-43.
Вопросы для самоконтроля
1. С помощью каких исходных аналитических зависимостей находят определяющие критерии?
2. Какой критериальной зависимостью следует воспользоваться для определения a при вынужденном движении жидкости в трубках теплообменника?
3. Какая критериальная зависимость применима для определения a при свободном конвективном теплообмене?
4. Как влияет характер движения жидкости (ламинарный, турбулентный) на выбор критериального уравнения, с помощью которого подсчитывается коэффициент теплоотдачи a?
5. По каким показателям определяют возможность применения того или иного критериального уравнения для подсчета коэффициента теплоотдачи a?
