Формы представления численных данных в ЭВМ

В ЭВМ данные помещается в ОЗУ, которая разбита на ячейки. Данные записываются в память в одной и той же форме.

Для записи чисел используется две формы:

естественная форма записи (с фиксированной точкой),

нормальная форма (с плавающей точкой).

Коды хранения числовых данных в ОЗУ. Числа, представленные в естественной форме (числа с фиксированной запятой), в ОЗУ хранятся в дополнительном коде.

Числа, представленные в нормальной форме (числа с плавающей запятой) хранятся в ОЗУ в прямом коде. Пример: 1 25,47= 12,547*10³, 1,2547* 10⁴ .

Машинные коды чисел. В ЭВМ независимо от того, в какой форме представлено число, числа хранятся специальных кодах, которые бывают прямыми, обратными и дополнительными.

Прямой код - применяется для записи положительных и отрицательных чисел, предназначенных для хранения в ОЗУ, а также для выполнения арифметических действий с положительными числами.

Обратный и дополнительный коды используются для представления отрицательных чисел при выполнении арифметических операций.

Обратный код (промежуточный) – для преобразования чисел в дополнительный код. Обратный код отрицательного двоичного числа получается из прямого кода положительного числа путем инвертирования, т.е. замена 0 на 1 и 1 на 0.

Дополнительный код образуется путем добавления (прибавления) единицы к младшему разряду обратного кода. Служит для выполнения арифметических действий с отрицательными числами.

Пример: Число 5₁₀⁼1012

прямой код 00000101

обратный код 11111010

дополнительный код 11111011

Действия над числами в естественной форме(числа с фиксированной точкой). Естественные числа - это числа с фиксированной запятой.

Рассмотрим на примерах.

Выполним действия с числами 75 и 28 в двоичной СС. Для этого выразим исходные числа в двоичной СС:

75₁₀=01001011₂

28₁₀=00011100₂

Сложить 75+28.

75₁₀=01001011₂ 0 1 0 0 1 0 1 1

28₁₀=00011100₂+ 0 0 0 1 1 1 0 0

0 1 1 0 0 1 1 1 = 103₁₀.

Вычесть 75-28(Вычитаемое меньше уменьшаемого).

75₁₀=01001011₂

28₁₀=00011100₂

Правило.

1)отрицательное число 28 для проведения с ними арифметических действий должно быть переведено в дополнительный код.

Прямой код числа 28 – 00011100

Обратный 11100011

Дополнительный 11100100

2)затем производится сложение прямого кода первого числа и дополнительного кода второго числа, причем недостающие разряды в дополнительном коде дополняются единицами.

00101111-число 47₁₀

Вычесть 28-75(Уменьшаемое меньше вычитаемого).

Прямой код 75 - 01001011

Обратный10110100+10110101

Дополнительный 10110101 (-75) 0 0 0 1 1 1 0 0

1 1 0 1 0 0 0 1

Число получилось отрицательное. Чтобы перевести его в прямой код, машина вычитает из младшего разряда единицу (получается 1 0 1 0 0 0 0) и инвертирует, т.е. меняет нули на единицы и единицы на нули (1 0 1 1 1 1).

Действия над числами в нормальной форме
числа с плавающей точкой.

Правило. Сложение производится путем сложения дробной и целой частей чисел как сложение целых чисел, причем порядок слагаемых должен быть одинаков, (т.е. во всех числах количество знаков (разрядов) в целой и в дробной частях должно быть равным). За общий порядок принимается наибольший. В дробной части числа недостающие разряды надо заполнить нулями справа, а в целой части числа недостающий разряды дополняют нулями слева, иначе можно сказать так: запятые должны располагаться под запятыми, как при записи сложения в столбик.

Практические задания

Вариант №1

1. Число 356₁₀ перевести в другие системы счисления.

2. Выполнить действия:

а) 11110111₂+1010101011₂

б) 110011₂-10101₂

в) 3567₈+4534₈

Вариант №2

1. Число 476₁₀ перевести в другие системы счисления.

2. Выполнить действия:

а) 10101011₂+11100011₂

б) 101011₂-10111₂

в) 7645₈+4444₈

Вариант №3

1. Число376₈ перевести в другие системы счисления.

2. Выполнить действия:

а) 1100111₂+10001111₂

б) 1111111₂-100011₂

в) 6666₈+4444₈

Вариант №4

1. Число456₈ перевести в другие системы счисления.

2. Выполнить действия:

а) 11101₂+111111₂

б) 1111111₂-100100₂

в) 7564₈+6543₈

Вариант №5

1. Число 432₈ перевести в другие системы счисления.

2. Выполнить действия:

а) 10101010₂+111100₂

б) 10000111₂-111111₂

в) 5555₈+6666₈

Вариант №6

1. Число 563₈ перевести в другие системы счисления.

2. Выполнить действия:

а) 10101011₂+1111001₂

б) 1111111₂-101010₂

в) 4444₈+5675₈

Вариант №7

1. Число 423₈ перевести в другие системы счисления.

2. Выполнить действия:

а) 101111₂+11111₂

б) 1111111₂-100001₂

в) 4536₈+7627₈

Вариант №8

1. Число321₁₀ перевести в другие системы счисления.

2. Выполнить действия:

а) 100111₂+111110₂

б) 1000001₂-11011₂

в) 5555₈+7777₈

Вариант №9

1. Число789₁₀ перевести в другие системы счисления.

2. Выполнить действия:

а) 10101011₂+111111₂

б) 10101011₂-111111₂

в) 5454₈+3636₈

Вариант №10

1. Число543₈ перевести в другие системы счисления.

2. Выполнить действия:

а) 10101111₂+110011₂

б) 11111000₂-111100₂

в) 3344₈+4567₈

Контрольные вопросы

1. Какие СС называются непозиционными?

2. Приведите примеры непозиционных СС.

3. Назовите коды хранения чисел в ОЗУ.

4. Назовите формы представления чисел.

5. Что такое «машинные» коды чисел? Какие из них вам известны?

6. Какие СС называются позиционными ?

7. Чем характеризуются позиционные СС?

8. Что такое «нормальная» форма представления чисел?

9. Приведите правило вычитания чисел в естественной форме.

10. Что такое «основание системы»?

11. Что такое прямой, обратный, дополнительный коды представления чисел.

12. Что такое «естественная форма чисел»? Что такое «нормальная форма чисел»?

13. Приведите правило сложения чисел нормальной форме (числа с плавающей точкой)

14. Дать определение системы счисления. Назвать и охарактеризовать свойства системы счисления.

15. Какие символы используются для записи чисел в двоичной системе счисления, восьмеричной, шестнадцатеричной (т.е. какие "рабочие числа" в этих СС)?

16. Что такое система счисления?

17. Чем отличаются позиционные системы счисления от непозиционных, в чем их преимущества?

Содержание отчета

1. Тема, цель.

2. Решение практических заданий по вариантам.

3. Вывод.

Лабораторная работа №3

Тема:Приемы использования основных алгоритмических структур.

Цели: Приобрести навыки применения различных видов алгоритмов.

Ход работы

1. Изучить теоретическую часть.

2. Выполнить практические задания.

3. Ответить на контрольные вопросы.

4. Оформить отчет.

Теоретическая часть

Алгоритм - это последовательность команд, ведущих к какой-либо цели.

Это строго определенная процедура, гарантирующая получение результата за конечное число шагов. Это правило, указывающее действия, в результате цепочки которых происходит переход от исходных данных к искомому результату. Указанная цепочка действий называется алгоритмическим процессом, а каждое отдельное действие - его шагом. Пример: площадь прямоугольника S=a*b.

Виды алгоритмов: вычислительные, диалоговые, графические, обработки данных, управления объектами и процессами и др.

Свойства алгоритмов – однозначность (и определенность), результативность (и выполнимость), правильность (и понятность), массовость или универсальность (т.е. применимость для целого класса задач, к различным наборам исходных данных).

Способы записи алгоритмов:

В виде блок-схем, в виде программ, в виде текстовых описаний (рецепты, например, рецепты приготовления пищи, лекарств и др.).

Основные алгоритмические конструкции и их описание средствами языков программирования.

Наиболее понятно структуру алгоритма можно представить с помощью блок-схемы, в которой используются геометрические фигуры (блоки), соединенные между собой стрелками, указывающими последовательность выполнения действий. Приняты определенные стандарты графических изображений блоков. Например, команду обработки информации помещают в блок, имеющий вид прямоугольника, проверку условий - в ромб, команды ввода или вывода - в параллелограмм, а овалом обозначают начало и конец алгоритма.

Структурной элементарной единицей алгоритма является простая команда, обозначающая один элементарный шаг переработки или отображения информации. Простая команда на языке схем изображается в виде функционального блока.

Структурный подход к разработке алгоритмов определяет использование только базових алгоритмических структур (конструкций): следование, ветвление, повторение, которые должны бать оформлены стандартным образом.

Рассмотрим основне структуры алгоритма:

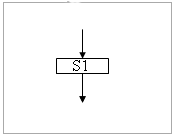	Данный блок имеет один вход и один выход. Из простых команд и проверки русловий образуются составные команды, имеющие болем сложную структуру и тоже один вход и один выход.
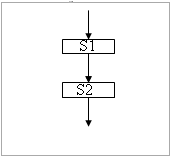	Команда следования состоит только изпростых команд. На рисунке простые команды имеют условное обозначение S1 и S2. Из команд следования образуются линейные алгоритмы. Примером линейного алгоритма будет нахождение суммыдвух чисел, введенных с клавиатуры.
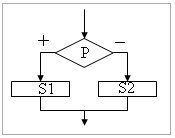	Команда ветвления – это составная команда алгоритма, в которой в зависимости от условия Р выполняется или одно S1, или другое S2 действие. Из команд следования и команд ветвления составляются разветвляющиеся алгоритмы (алгоритмы ветвления). Примером разветвляющегося алгоритма будет нахождение большего из двух чисел, введенных с клавиатуры.
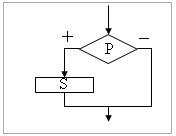	Команда ветвления может бать полной и неполной формы. Неполная форма команды ветвления используется тогда, корда не обходимо выполнять действие S только в случае соблюдения условия P. Если условие P не соблюдается, то команда ветвления завершает свою работу без выполнения действия. Примером команды ветвления неполной формы будет уменьшение в два раза только четного числа.
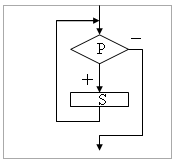	Команда повторения – это составная команда алгоритма, в которой в зависимости от условия Р возможно многократное выполнение действия S. Из команд следования и команд повторения составляются циклические алгоритмы (алгоритмы повторения). На рисунке представлена команда повторения с предусловием. Называется она так потому, что вначале проверяется условие, а уже затем выполняется действие. Причем действие выполняется, пока условие соблюдается. Пример циклического алгоритма может бать следующий. Пока с клавиатуры вводяться положительные числа, алгоритм выполняет нахождение их суммы. Команда повторения с предусловием не является единственно возможной. Разновидностью команды повторения с предусловием является команда повторения с параметром. Она используется тогда, корда известно количество повторений действия. В блок-схеме команды повторения с параметром условие записывается не в ромбе, а в шестиугольнике. Примером циклического алгоритма с параметром будет нахождение суммы первых 20 натуральных чисел.
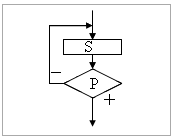	В команде повторения с постусловием вначале выполняется действие S и лиш затем, проверяется условие P. Причем действие повторяется до тех пор, пока условие не соблюдается. Примером команды повторения с постусловием будет уменьшение положительного числа до тех пор, пока оно неотрицательное. Как только число становится отрицательным, команда повторения заканчивает свою работу. С помощью соединения только этих элементарных конструкций (последовательно или вложением) можно "собрать" алгоритм любой степени сложности.

Линейный алгоритм

Приведем пример записи алгоритма в виде блок-схемы, псевдокодов и на языке Паскаль.

Использование логических высказываний и операций в алгоритмических конструкций.

В записи логических выражений помимо арифметических операций сложения, вычитания, умножения, деления и возведения в степень используются операции отношения < (меньше), <= (меньше или равно), > (больше), >= (больше или равно), = (равно), <> (не равно), а также логические операции и, или, не.

Решение любой задачи на ЭВМ можно разбить на следующие этапы: разработка алгоритма решениязадачи, составление программы решения задачи на алгоритмическом языке, ввод программы в ЭВМ, отладка программы (исправление ошибок), выполнение программы на ПК, аналаз полученных результатов.

Первый этап решения задачи состоит в разработке алгоритма.

Алгоритм – это точная конечная система правил, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения после конечного числа шагов искомого результата.

Алгоритм может быть описан одним из трех способов:

- словесным (пример в начале раздела);

- графическим (виде специальной блок-схемы);

- с помощью специальных языков программирования.

Блок-схема – распространенный тип схем, описывающий алгоритмы или процессы, изображая шаги в виде блоков различной формы, соединенных между собой стрелками.

Практическая часть

Задание 1. Определить площадь трапеции по введенным значениям оснований (a и b) и высоты (h). Запись алгоритма в виде блок-схемы (рисунок 1): а = 3; b = 2; h = 2.

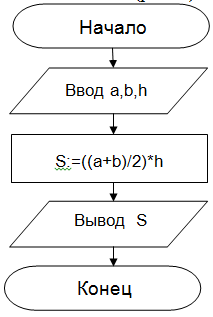
Рисунок 1. Блок-схема линейного алгоритма

Задание 2.Определить среднее арифметическое двух чисел, если a положительное и частное (a/b) в противном случае. Запись алгоритма в виде блок-схемы (рисунок 2):

1) a = 3; b = 5.

2) а = -3; b = 5.

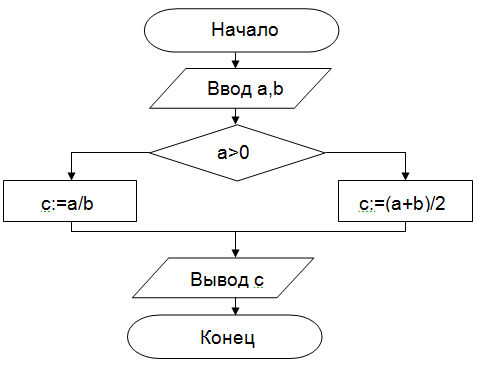
Рисунок 2. Блок-схема алгоритма с ветвлением

Задание 3. Составить алгоритм нахождения суммы целых чисел в диапазоне от 1 до 10. Запись алгоритма в виде блок-схемы (рисунок 3):

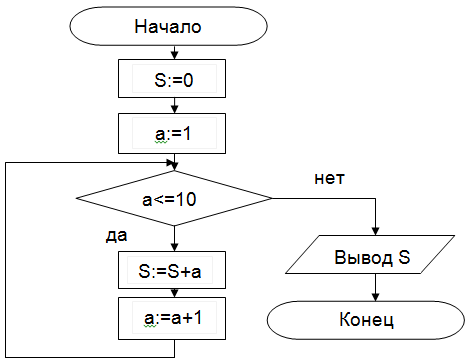
Рисунок 3. Циклический алгоритм с предусловием

Задание 4.В алгоритме с постусловием сначала выполняется тело цикла, а затем проверяется условие окончания цикла. Решение задачи нахождения суммы первых десяти целых чисел. Запись алгоритма в виде блок-схемы (рисунок 4):

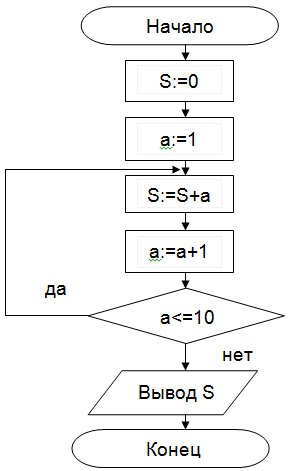
Рисунок 4. Циклический алгоритм с постусловием

Задание 5. Построить линейный алгоритм вычисления значения У по формуле У=(7Х+4)*(2Х-2) при Х=3. Составьте алгоритм самостоятельно, выделяя каждое действие как отдельный шаг (для оценки «отлично»).

Контрольные вопросы

1. Что такое алгоритм?

2. Какие способы записи алгоритмов вы знаете?

3. Какие свойства алгоритмов Вам известны?

4. Составьте алгоритм приготовления любого блюда?

5. Постройте блок-схему на составленный алгоритм?

Содержание отчета

4. Тема, цель.

5. Решение практических заданий.

6. Вывод.

Лабораторная работа №4

Тема:Приемы использования табличных величин (массивы).

Цели: Научиться применять табличные величины.

Ход работы

1. Изучить теоретическую часть.

2. Выполнить практические задания.

3. Ответить на контрольные вопросы.

4. Оформить отчет.

Теоретическая часть

Наиболее широко известная структура данных – массив.

Массив состоит из компонент одного типа, называемого базовым. Поэтому структура массивов однородна.

Кроме того, массивы относят к так называемым структурам с прямым доступом. Для того чтобы обозначить отдельную компоненту, к имени всего массива добавляется индекс. Индекс – это значение специального типа, определенного как тип индекса массива. Количество индексов называется размерностью массива. Отметим, что в памяти ПЭВМ каждой компоненте массива отводится отдельное поле равных размеров, при этом, все элементы массива расположены подряд. Если x является переменной-массивом размерности n, то отдельная компонента обозначается с помощью имени массива, за которым следует индекс требуемой компоненты – i x. Иногда компоненты массивов называют переменными с индексами.

Обычный прием работы с массивами, в особенности с большими массивами – выборочное изменение отдельных его компонент, а не конструирование полностью нового составного значения. При этом переменная-массив рассматривается как массив составляющих переменных, и возможно присваивание значений отдельным компонентам, например, x_i ← 0,456. Тот факт, что индексы массива относятся к определенному (скалярному) типу, имеет важное следствие: индексы массива можно вычислять. На место индексирующей константы можно подставлять любое индексирующее выражение; оно будет вычислено, и результат идентифицирует требуемую компоненту. Если необходимо выполнить некоторую операцию над всеми 30 компонентами массива или над соседними компонентами некоторой части массива, то удобно воспользоваться циклом.

Индексация элементов массива в большинстве случаев производится от нуля.

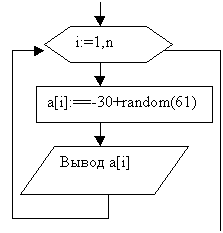
Рисунок 1 – Пример заполнение одномерного массива случайным образом

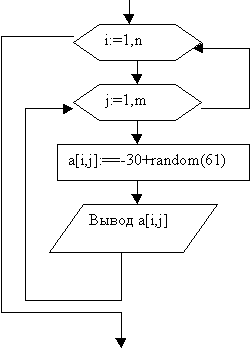
Рисунок 2 – Пример заполнение двумерного массива

случайным образом

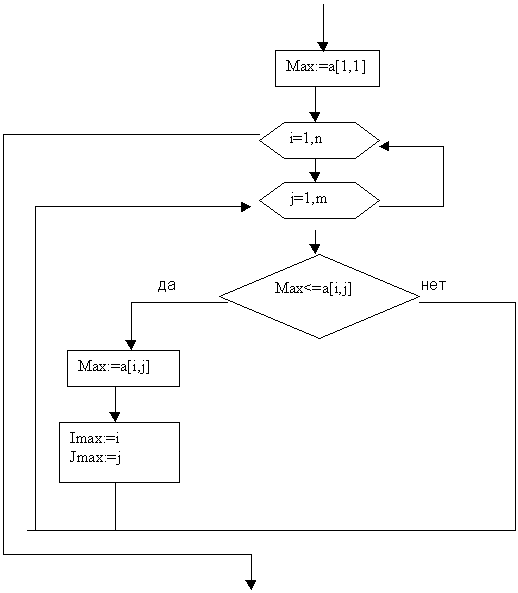
Рисунок 3 – Блок-схема нахождения максимального

элемента

Одномерные массивы

Одномерный массив – это непрерывный участок памяти, содержащий последовательность объектов одинакового типа, обозначаемый одним именем.

Массив характеризуется следующими основными понятиями:

Элемент массива (значение элемента массива) – значение, хранящееся в определенной ячейке памяти, расположенной в пределах массива, а также адрес этой ячейки памяти.

Каждый элемент массива характеризуется тремя величинами:

- адресом элемента - адресом начальной ячейки памяти, в которой расположен этот элемент;

- индексом элемента (порядковым номером элемента в массиве);

- значением элемента.

Адрес массива – адрес начального элемента массива.

Имя массива – идентификатор, используемый для обращения к элементам массива.

Размер массива – количество элементов массива

Размер элемента – количество байт, занимаемых одним элементом массива.

Графически расположение массива в памяти компьютера можно представить в виде непрерывной ленты адресов.

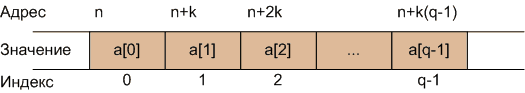
Рисунок 4 – Графически расположение массива

в памяти компьютера

Представленный на рисунке массив содержит q элементов с индексами от 0 до q-1. Каждый элемент занимает в памяти компьютера k байт, причем расположение элементов в памяти последовательное.

Адреса i-го элемента массива имеет значение n+k·i

Адрес массива представляет собой адрес начального (нулевого) элемента массива. Для обращения к элементам массива используется порядковый номер (индекс) элемента, начальное значение которого равно 0. Так, если массив содержит q элементов, то индексы элементов массива меняются в пределах от 0до -1.

Длина массива – количество байт, отводимое в памяти для хранения всех элементов массива.

ДлинаМассива = РазмерЭлемента * КоличествоЭлементов

Многомерные массивы. В языке Си могут быть также объявлены многомерные массивы. Отличие многомерного массива от одномерного состоит в том, что в одномерном массиве положение элемента определяется одним индексом, а в многомерном – несколькими. Примером многомерного массива является матрица.

Общая форма объявления многомерного массива будет расположен в памяти следующим образом

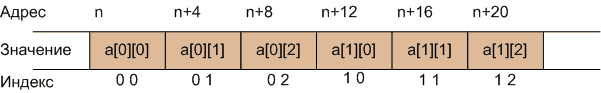
Рисунок 5 – Графически расположение массива

в памяти компьютера

Общее количество элементов в приведенном двумерном массиве определится как

КоличествоСтрок * КоличествоСтолбцов = 2 * 3 = 6.

Количество байт памяти, требуемых для размещения массива, определится как

КоличествоЭлементов * РазмерЭлемента = 6 * 4 = 24 байта.

Инициализация многомерных массивов. Значения элементов многомерного массива, как и в одномерном случае, могут быть заданы константными значениями при объявлении, заключенными в фигурные скобки {}. Однако в этом случае указание количества элементов в строках и столбцах должно быть обязательно указано в квадратных скобках [].

Однако чаще требуется вводить значения элементов многомерного массива в процессе выполнения программы. С этой целью удобно использовать вложенный параметрический цикл.

Контрольные вопросы

1. Что такое массивы?

2. Какие бывают массивы?

3. Что такое одномерный массив?

4. Что такое двумерный массив?

5. Общая форма объявления одномерного массива?

6. Общая форма объявления многомерного массива?

7. Общее количество элементов одномерном массиве?

Содержание отчета

1. Тема, цель.

2. Решение практических заданий.

3. Вывод.

Лабораторная работа №5

Тема:Формальное исполнение фрагментов алгоритма (программы) и исправление допущенных ошибок.

Цели: Научиться применять необходимые фрагменты алгоритма и выявить допущенные ошибки.

Ход работы

1. Изучить теоретическую часть.

2. Выполнить практические задания.

3. Ответить на контрольные вопросы.

4. Оформить отчет.

Теоретическая часть

Алгоритмы и их свойства. Под алгоритмом понимают понятное и точное предписание (ука­зание) исполнителю совершить конечную последовательность однознач­но трактуемых действий, направленных на решение поставленной зада­чи.

Понятие алгоритма относится к числу фундаментальных математических понятий. Термин "алгоритм" происходит от имени узбекского математика IX века Аль-Хорезми, который разработал правила выполнения четырех ариф­метических действий над числами в десятичной системе счисления. Сово­купность этих правил в Европе стали называть "алгоритм". Впоследствии слово переродилось в "алгоритм" и в 30-х годах XX века понятие алгоритма стало объектом математического изучения, а с появлением ЭВМ получило широкую известность.

Свойства алгоритма

1. Дискретность – каждый алгоритм – это последовательность четко разде­ленных друг от друга команд, образующих дискретную (прерывистую) струк­туру. Только выполнив одну команду можно перейти к другой.

2. Определенность (детерминированность) – каждая команда понятна ис­полнителю, однозначно им трактуема, не возникает разночтений в трактовке порядка выполнения команд.

3. Массовость – один и тот же алгоритм может быть использован для реше­ния целого класса однотипных задач.

4. Результативность – алгоритм всегда приводит за конечное число дейст­вий к правильному решению в случае точного его исполнения.

5. Однозначность- при одних и тех же условиях алгоритм должен приводить к од­ному результату.

Способы описания алгоритмов. Существует несколько способов записи алгоритмов, отличающихся друг от друга наглядностью, компактностью, степенью формализации. Спо­соб записи алгоритма – это язык определенных символов, правил и т.д. Естественный человеческий язык не является формализованным, и поэтому может содержать выражения, имеющие неоднозначный смысл. По­добные явления должны быть полностью исключены в языках, используемых для общения с исполнителями-автоматами. Приходится соблюдать ряд требований:

- при формулировании предписаний можно требовать от исполнителя вы­полнения лишь тех операций, которые жестко определены для данного исполнителя;

- можно использовать лишь принятые для языка исполнителя правила построения предписаний;

- нельзя использовать ничего не предусмотренного правилами, ибо испол­нитель все равно такие предписания не выполнит.

Формализация языка обедняет его выразительные способности по сравнению с естественным языком человека. Основными способами описания алгоритмов являются:

1) словесный;

2) табличный;

3) графический;

4) программа.

Словесный способ описания алгоритмов ориентирован, прежде всего, на исполнителя-человека и допускает различные варианты записи указаний (команд). Но при этом запись должна быть достаточно точна, чтобы человек-исполнитель мог понять суть команд и выполнить их. Один из недостатков этого способа – многословие. Но этот способ описания алго­ритмов обладает и большой универсальностью: словами можно выразить то, что нельзя записать с помощью формул. А это особенно ценно при рабо­те с алгоритмами не вычислительных процессов.

Примеры: инструкция сборки шкафа, велосипеда, порядок постройки дома, рецепт приготовления торта.

Табличный способ описания алгоритма удобен при массовых вычислениях по одной и той же формуле.

Пример: вычислить значение функции 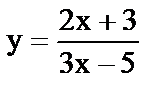при разных значениях аргумента х.

x	2x	2x + 3	3x	3x – 5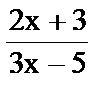
					1.3
-3	-6	-3	-9	-14	0.21428...
				-5	-0.6

Графический способ описания предполагает запись алгоритма в виде блок-схемы.

Блок-схема – это способ представления алгоритма с помощью геометриче­ских фигур заданного набора, изображающих отдельные шаги алгоритма и соединенных между собой линиями (стрелками), указывающими порядок реализации алгоритма.

Для изображения блок-схемы любого алгоритма ограничимся сле­дующим набором геометрических фигур:

начало конец	или		начало (конец) алгоритма
	выполнение действий
	ввод (вывод) данных
	проверка условия
	подпрограмма
	начало цикла

Графический способ записи отличается наглядностью и очень полез­ен на начальной стадии разработки алгоритма.

Программа представляет собой способ записи алгоритма с помощью операторов (команд) языка программирования (Паскаль, Бейсик, Cи++, Фортран, Пролог, Ассемблер)

Структурный подход к составлению алгоритмов. Каждый алгоритм должен быть: легко воспринимаемым, легко проверяемым и допускать возможность его модификации без существенной перестройки всей структуры. Реализовать эти требования позволяет структурный подход к разработке алгоритма, который состоит в следующем: любой алгоритм может быть реализован в виде комбинации трех ба­зовых алгоритмических структур: линейной, разветвляющейся и циклической.

1. Линейная структура обеспечивает выполнение команд или операторов последовательно друг за другом

P1

P2

Pn

P3

. . .

2. Разветвляющаяся структура обеспечивает выполнение одной из последовательностей действий (P₁ или P₂) в зависимости от выполнения условия S:

альтернатива (полная конструкция) ЕСЛИ S ТО P1 ИНАЧЕ P2. P1 S P2 да нет

коррекция (неполная конструкция) ЕСЛИ S ТО P   P S да нет

3. Циклическая структура обеспечивает многократное повторение последовательности действий в зависимости от определенного условия (повторяй пока условие истинно) или определенное число раз (повторяй 15 раз).

P

S

да

нет

Так как каждая структура имеет один вход и один выход, то допускается неограниченное соединение этих структур и их вложение друг в друга. Это позволяет проектировать сложные алгоритмы.

Формальное исполнение алгоритма. Текст, написанный на любом языке, состоит из предложений, выражающих законченную мысль. Алгоритмы, ориентированные на исполните­ля, состоят из предложений, но не всякое предложение можно исполь­зовать в программе, ведь исполнитель понимает любой текст буквально, а переносимый смысл предложений до него не доходит.

Исполнитель действует по алгоритму формально, т.е. механически выполняет все команды алгоритма, не вникая в их смысл.

Для проверки необходимо формальное испол­нение алгоритма. При этом действовать надо строго механически, следуя инструкциям. Формальное исполнение алгоритма позволяет обнаружить ошибки и определить пути их исправления.

Этапы решения задачи с помощью компьютера. Решение задач с помощью компьютера можно разделить на несколько этапов.

1. Формулировка задачи.

2. Составление математической модели.

Прежде чем решать задачу с помощью компьютера необходимо разработать ее модель, т.е. выделить наиболее существенные признаки задачи. Мы будем использовать математическое моделирование – составление модели задачи с помощью математических символов. Т.о. составить математическую модель – это значит записать последовательно все формулы, используемые для решения задачи.

3. Построение алгоритма решения задачи.

На этом этапе, используя словесный способ, составляется алгоритм решения задачи.

4. Описание величин.

Вводится буквенное обозначение величин, с пояснением и указанием вида величины (исходная, промежуточная или результат).

5. Построение блок-схемы (переход от словесного способа к графическому).

6. Составление программы (перевод алгоритма на язык программирования).

7. Трансляция программы, получение и анализ результатов, корректировка программы.

Практическая часть

Привести примеры алгоритмов, которые можно описать:

а) линейной структурой;

б) разветвляющейся структурой;

в) циклической структурой.

Контрольные вопросы

1. Что такое алгоритм? Кто может быть исполнителем алгоритма?

2. Дайте характеристику основным свойствам алгоритма. К чему может привести невыполнение свойств алгоритма?

3. Что такое формализация?

4. Перечислите основные способы описания алгоритмов. Чем вызвано разнообразие способов записи алгоритмов?

5. Дайте характеристику и приведите примеры словесного и табличного способа.

6. Перечислите основные элементы блок-схемы и их назначение.

7. Назовите требования, предъявляемые к составлению алгоритма.

8. В чем суть структурного подхода к составлению алгоритмов?

9. Перечислите базовые алгоритмические структуры, изобразите их графически.

10. Какие типы алгоритмов вы знаете?

11. Что понимается под формальным исполнением алгоритма? В чём важность возможности формального исполнения алгоритма?

12. Перечислите основные этапы решения задач с помощью компьютера.

Содержание отчета

1. Тема, цель.

2. Решение практических заданий.

3. Вывод.

Лабораторная работа №6

Тема: Графический интерфейс ОС Windows. Стандартные и служебные приложения ОС.

Цели:Изучить графический интерфейс ОС Windows и стандартные и служебные приложения ОС.

Ход работы

1. Изучить теоретическую часть.

2. Выполнить практические задания.

3. Ответить на контрольные вопросы.

4. Оформить отчет.

Теоретическая часть

Операционная система Windows 7. Разработка Windows 7 (Seven) началась сразу после выпуска ОС Windows Vista.milestone 1, 2 и 3 были анонсированы Microsoft в 2008 году. Дата выхода Windows 7 в России - 22 октября 2009 года.

Операционная система Windows 7 – это новейшая производительная и надежная операционная система с новыми возможностями управления компьютером и файлами, которая позволяет выполнять на персональном компьютере привычные задачи намного быстрее и проще.

1. Загрузка ОС Windows 7, если она установлена на компьютер, происходит автоматически при каждом включении ПК. Если в компьютере установлено несколько версий Windows, т.е. имеет место многозагрузочная конфигурация, то можно выбрать, какая из версий будет запускаться по умолчанию. Можно также создать список автоматически запускаемых при загрузке системы Windows программ.

Завершение работы ОС Windows 7. Правильный алгоритм завершения работы с Windows 7 такой:

1. Закройте все приложения (все открытые окна). В подавляющем большинстве случаев это делается щелчком мышью по кнопке закрытия окна (в правом верхнем углу окна).

2. Щелкните мышью по кнопке Пуск.

3. В появившемся Главном меню щелкните мышью по кнопке Завершение работы.

В результате после некоторого ожидания система сама выключит электропитание вашего компьютера. После этого, не забудьте выключить питание монитора и дополнительных устройств, которые подключены к вашему компьютеру, если они имеют собственные кабели питания (некоторые устройства, подключенные к портам USB, питаются от компьютера).

2. Рабочий стол – это основная область экрана, которая появляется после включения компьютера и загрузки ОС Windows 7. На рабочий стол можно помещать значки различных объектов, например, файлов и папок, и выстраивать их в удобном порядке (рис. 1). Чтобы запустить какой-либо объект, необходимо дважды щелкнуть по его значку. Окна открытых программ и папок отображаются на рабочем столе.

Чтобы обеспечить быстрый доступ к файлам, папкам, программам и другим объектам с Рабочего стола можно создать для них ярлыки.

Ярлык - это средство для быстрого доступа к объекту. Он содержит ссылку (путь) на объект, а не сам объект. Двойной щелчок на ярлыке открывает объект, для которого он создан. При удалении ярлыка удаляется только ярлык, но не сам объект. Ярлык от значка самого объекта можно узнать по стрелке на нем.

Область рабочего стола иногда расширяют, включая в него Панель задач, которая располагается вдоль нижней границы экрана. В отличие от рабочего стола, который может быть закрыт открытыми окнами, панель задач видна почти всегда. Она состоит из трех основных частей:

- кнопка П