Расчет конечной температуры рабочих жидкостей

Выше конечной целью теплового расчете являлось определение поверхности нагрева и основных размеров теплообменника для его дальнейшего конструирования. Предположим теперь, что теплообменник уже имеется или по крайней мере спроектирован. В этом случае целью теплового расчета является определение конечных температур рабочих жидкостей. Это - так называемый поверочный расчет.

При решении такой задачи известными являются следующие величины: поверхность нагрева F, коэффициент теплопередачи k, водяные эквиваленты W₁ и W₂ и начальные температуры t₁’ и t₂’, а искомыми: конечные температуры t₁” и t₂” и количество переданного тепла Q.

В приближенных расчетах можно исходить из следующих представлений. Количество тепла, отдаваемое горячей жидкостью, равно:

(2.13)

откуда конечная температура ее t₁” определяется соотношением:

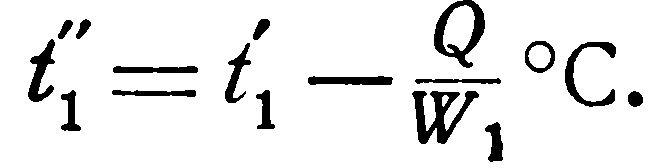(a)

Соответственно для холодной жидкости имеем:

(2.14)

и

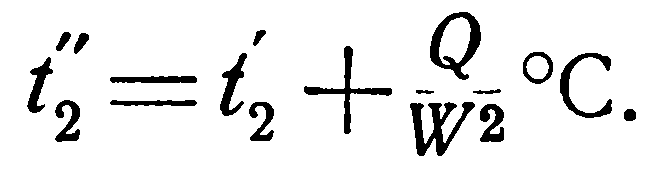(b)

Если принять, что температуры рабочих жидкостей меняются по линейному закону, то

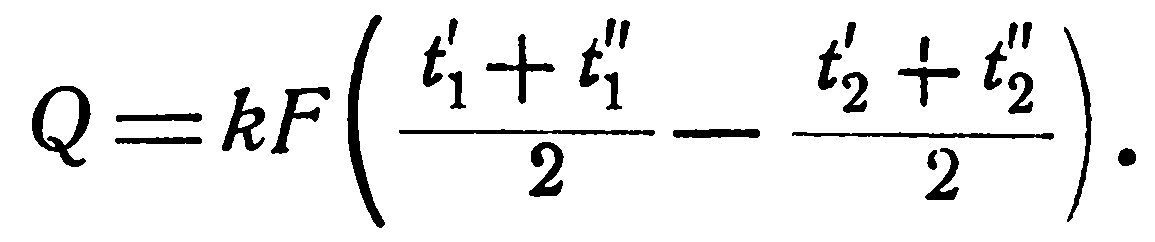(с)

Вместо неизвестных t₁” и t₂” подставим их значения из уравнений (а) и (b), тогда получим:

(d)

Произведя дальнейшее преобразование, имеем:

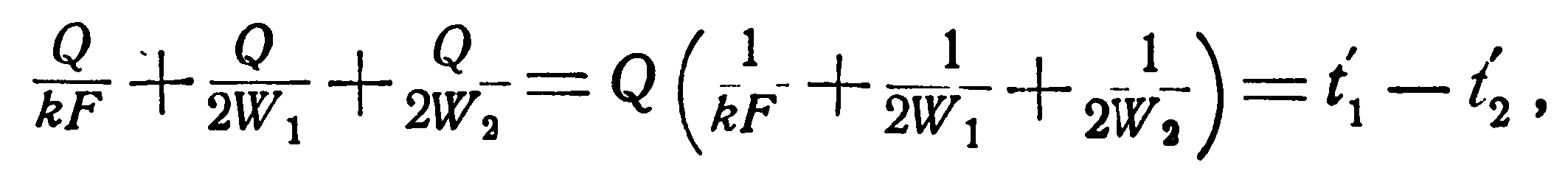(e)

откуда окончательно получаем:

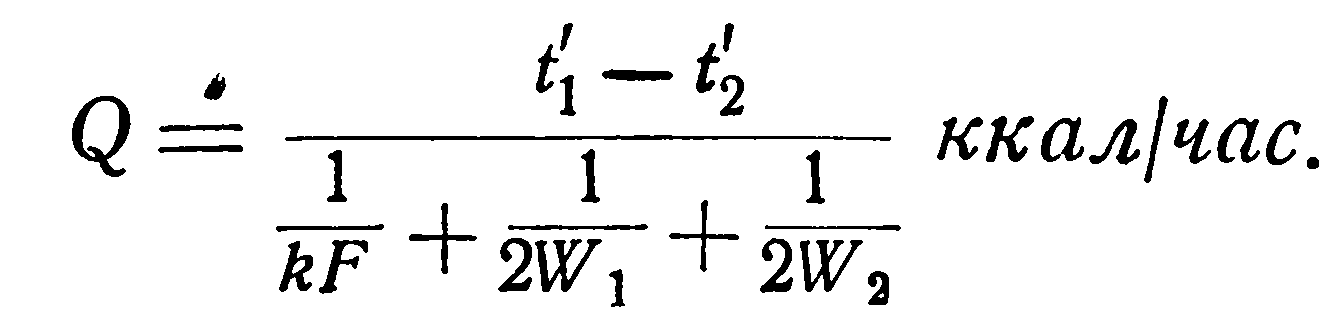(2.15)

Зная количество переданного тепла Q, очень просто формулам (а) и (b) определить и конечные температуры рабочих жидкостей t₁” и t₂”.

Приведенная схема расчета, хотя и проста, однако применима лишь для ориентировочных расчетов и в случае небольших изменений температур жидкостей. В общем же случае конечная температура зависит от схемы движения рабочих жидкостей. Поэтому для прямотока и противотока ниже приводится вывод более точных формул.

1. Прямоток. Выше было показано, что температурный напор изменяется по экспоненциальному закону:

(2.16)

Имея в виду, что

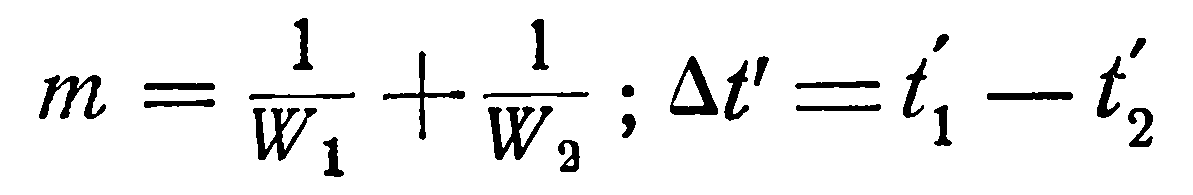
и, что в конце поверхности нагрева Δt” = t₁’ – t₂’, то, подставляя эти значения в уравнение (19), последнее можно представить в следующем виде:

(2.17)

Однако, это уравнение дает лишь разности температур. Чтобы отсюда получить конечные температуры в отдельности, необходимо обе части равенства вычесть из единицы:

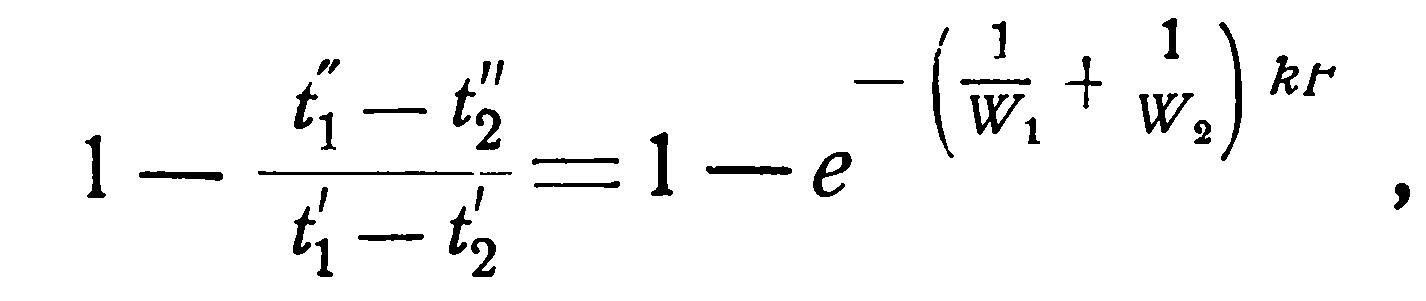(2.18)

или

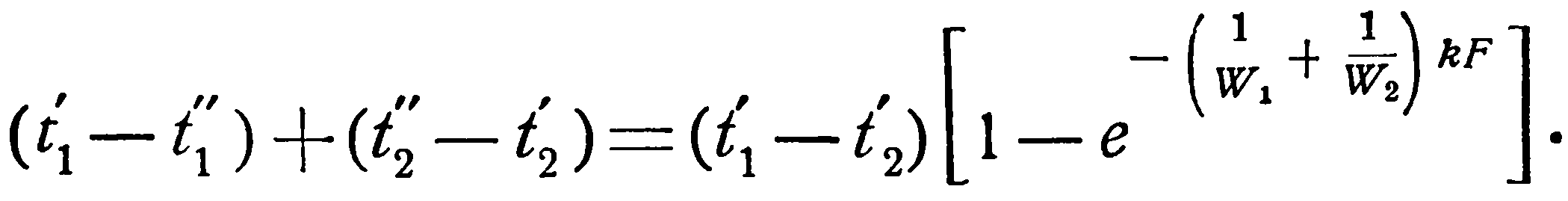(2.19)

Так как

[см. разд.2.1 уравнение (2.5)].

то, подставляя это значение в левую часть уравнения (2.19), получаем:

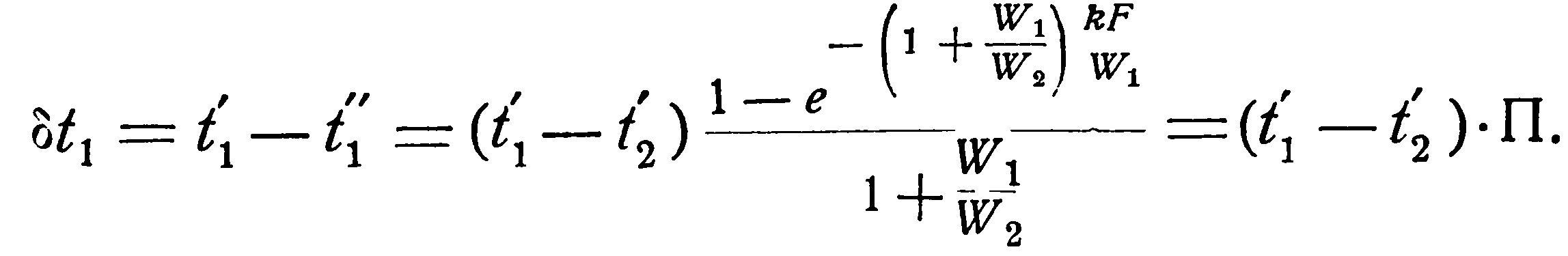(2.20)

Последнее уравнение, показывает, что изменение температуры горячей жидкости δt₁ равно некоторой доле П располагаемого начального температурного напора, t₁’ – t₂’; эта доля зависит только от двух безразмерных параметров и .

Аналогичным образом из уравнения (2.19) можно получить выражение и для изменения температуры холодной жидкости, а именно:

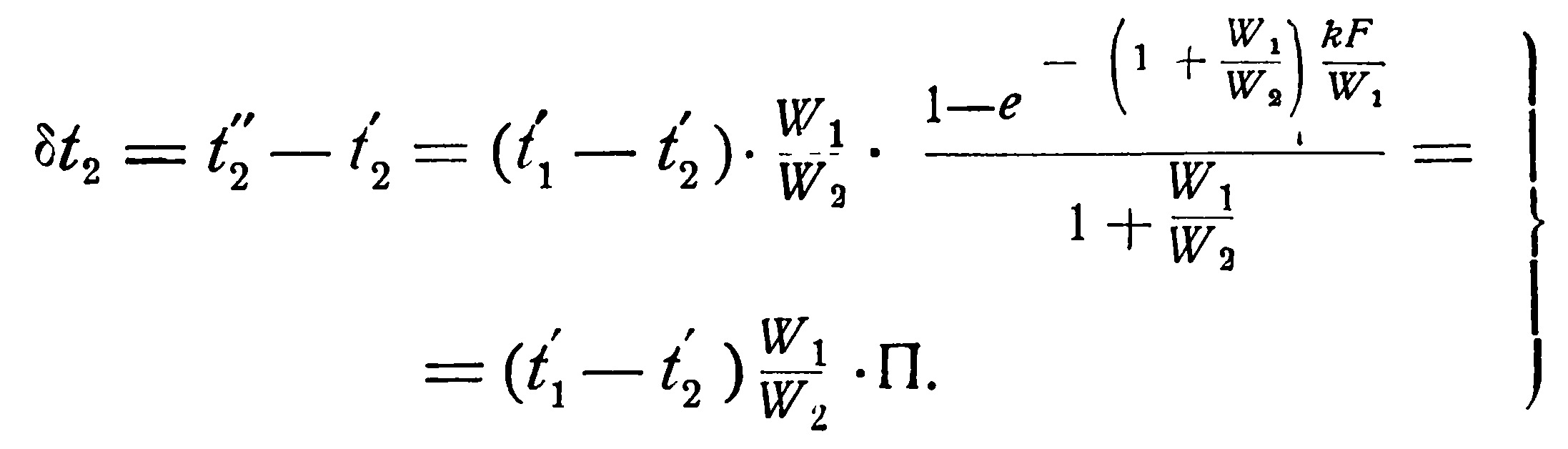(2.21)

Определив изменения температур рабочих жидкостей и зная их начальные температуры, легко определить конечные:

(2.22)

Расход тепла определяется путем умножения водяного эквивалента жидкости на изменение ее температуры:

(2.23)

Значение функции 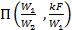приведено на рис. 2.5. Формулы (2.21) – (2.23) могут быть применены и для расчета промежуточных значений температуры рабочих жидкостей и количества тепла. В этом случае в, расчетные формулы вместо F надо подставить значение F_x.

Пример 2.2. Имеется водяной холодильник с поверхностью нагрева F=8 м². Определить конечные температуры жидкостей и часовое количество передаваемого тепла Q, если заданы следующие величины: V₁= 0,25 м³/час, γ₁ = 1100 кг/м³, c_p1 = 0,727 ккал/кг °С и t₁’ = 120 °С Для охлаждения в распоряжении имеется 1000 л воды в час при температуре t₂’ = 10 °С. Кроме того, известно значение коэффициента теплопередачи k = 30 ккал/м² час °С.

Соответствующее значение функции П находим из рис.2.5:

П (0,2; 1,20) = 0,64.

Рис. 2.5. 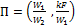- вспомогательная функция для расчета конечной температуры при прямотоке

Изменение (понижение) температуры горячей жидкости согласно уравнению (2.20) равно:

Следовательно, конечная температура ее равна:

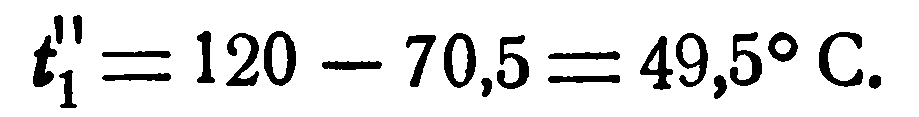
Количество переданного тепла в час определится по уравнению (2.23)

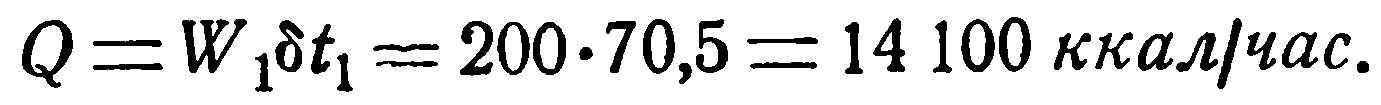
Изменение температуры холодной жидкости определяется по уравнению (2.21). Но его можно также определить и из соотношения Q = W₂ (t₂” - t₂’), откуда

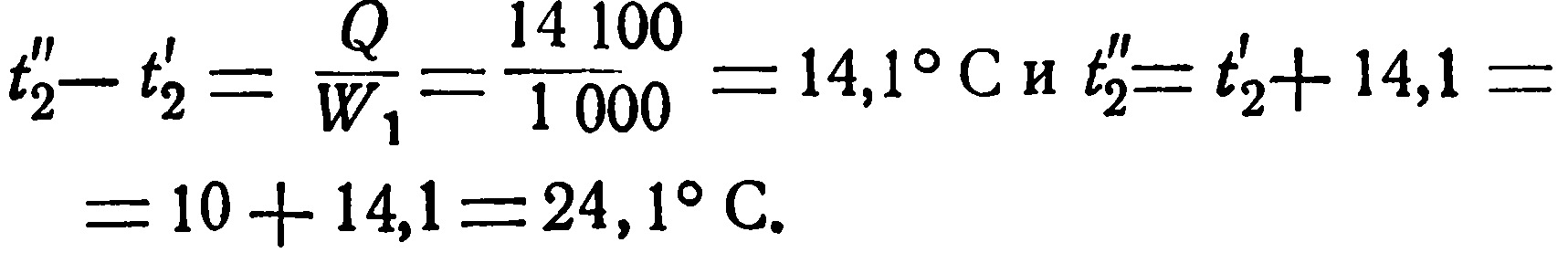
2. Противоток. Для противотока расчетные формулы выводятся так же, как и для прямотока. Окончательно они имеют следующий вид:

(2.24)

(2.25)

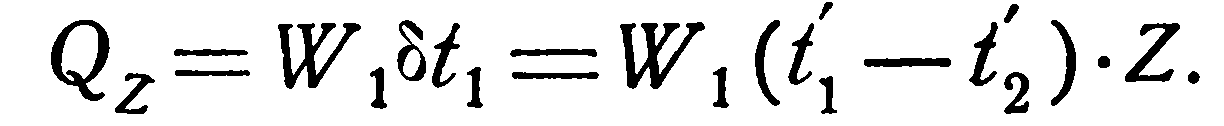(2.26)

В частном случае, когда формулы

(2.24) – (2.26) принимают вид:

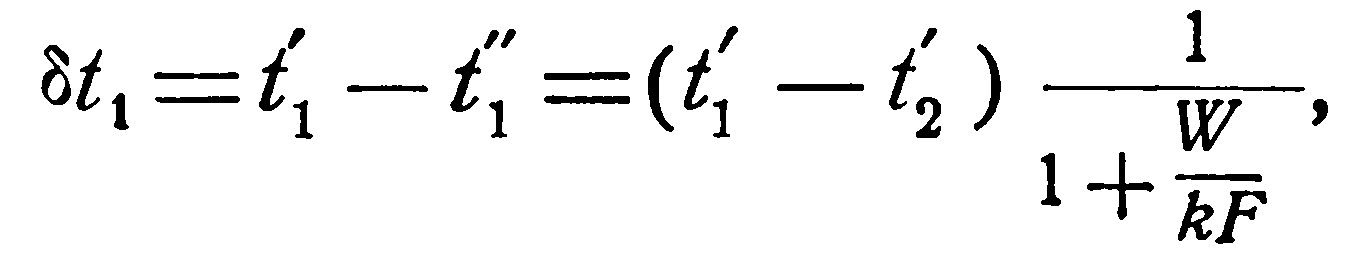(2.27)

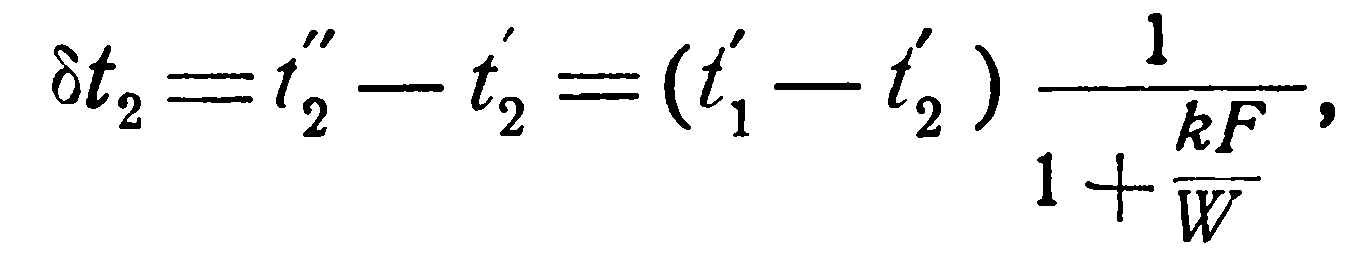(2.28)

(2.29)

Значение функции 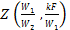приведено на рис. 2.6.

Рис. 2.6. 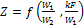- вспомогательная функция для расчета конечной температуры при противотоке

Для расчета промежуточных значений температуры рабочих жидкостей и количества переданного тепла в формулах (2.23) – (2.29) в числителе значение F заменяется на F_x, а в знаменателе остается значение полной поверхности F.

Пример 2.3. Если взять тот же теплообменник, который был рассмотрен в условиях прямотока, и допустить, что условия теплопередачи остаются без изменения (k = 30 ккал/м² час °С), то получим следующие соотношения:

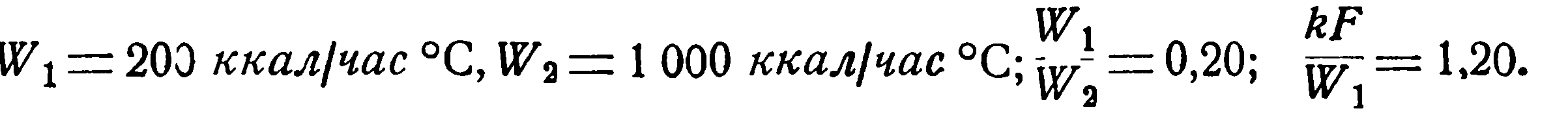
Из рис. 2.6 находим значение функции Z:

Z (0,20; 1,20) = 0,68.

Изменение температуры горячей жидкости равно [уравнение (2.24)]:

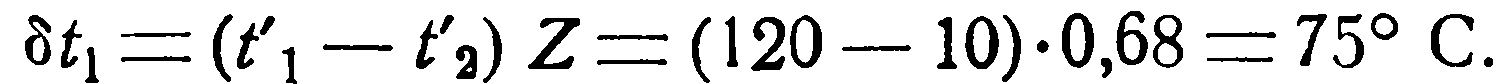
Конечная температура ее:

Изменение температуры холодной жидкости [уравнение (2.25)];

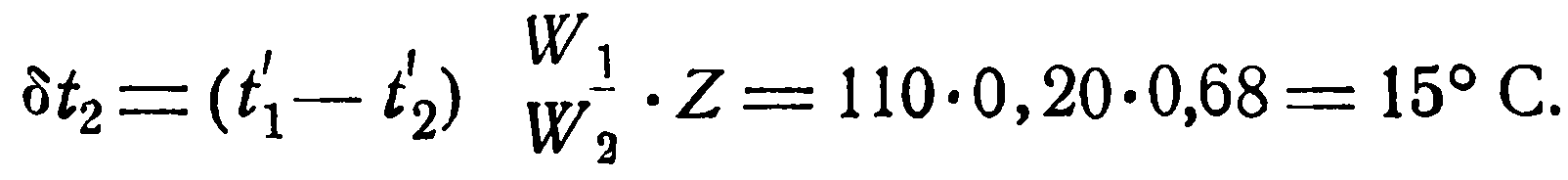
Конечная температура ее:

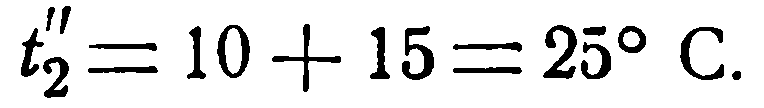
Количество переданного тепла в час [уравнение (2.26)]:

Таким образом, в случае противотока в теплообменнике происходит более глубокое охлаждение горячей жидкости.

3. Сравнение прямотока с противотоком. Чтобы выявить преимущество одной схемы перед другой, достаточно сравнить количество передаваемого тепла при прямотоке и противотоке при равенстве прочих условий. Для этого необходимо уравнение (2.23) разделить на уравнение (2.26). В результате этого действия мы получаем новую функцию тех же двух безразмерных аргументов

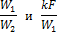
характер изменения которой графически показан на рис. 2.7.

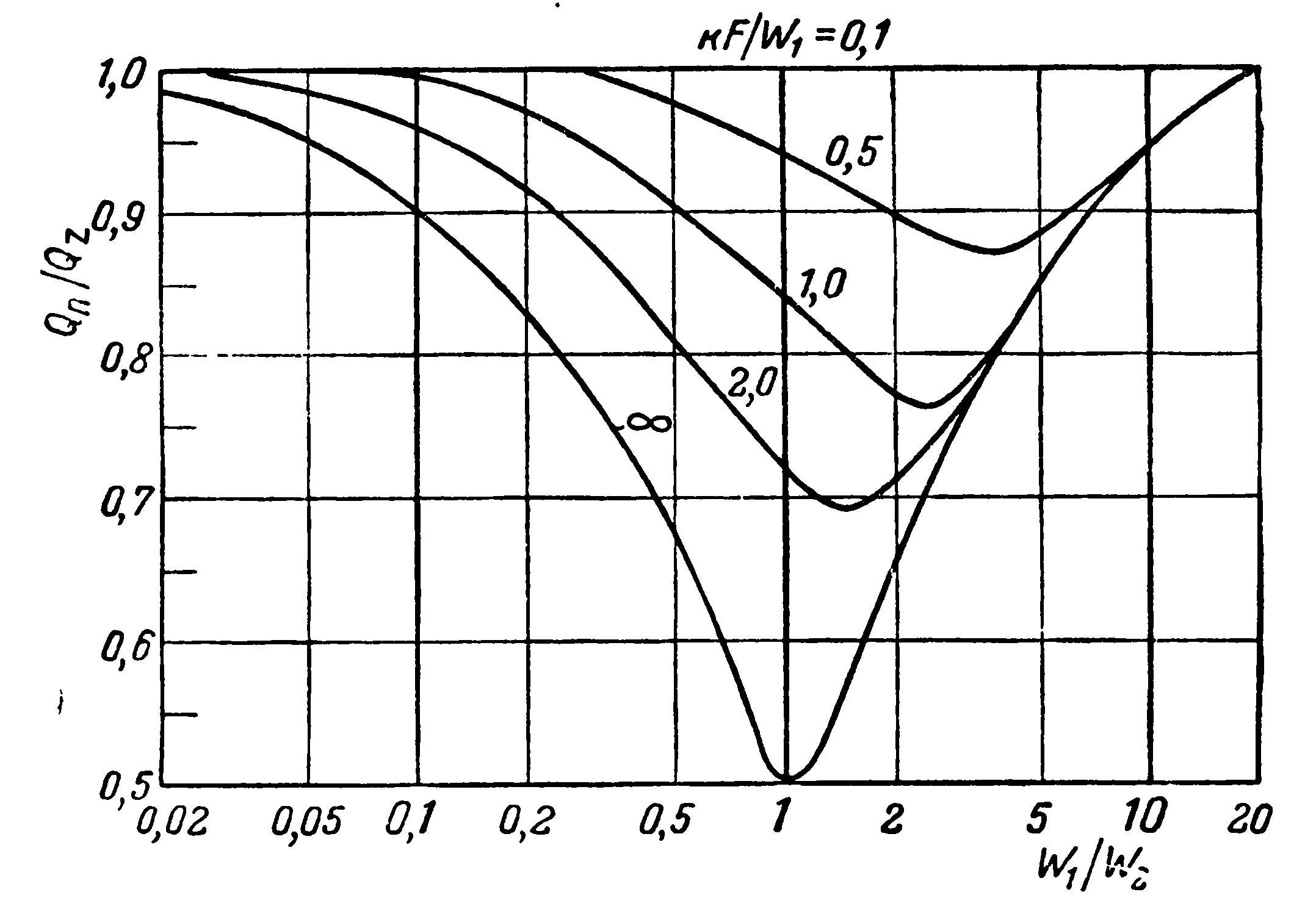
Рис. 2.7. -сравнение прямотока с противотоком

Из рисунка следует, что схемы можно считать равноценными в том случае, если водяные эквиваленты обеих жидкостей значительно отличаются один от другого (при и при ) или если значение параметра 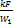- мало. Первое условие равнозначно тому, что изменение температуры одной жидкости незначительно по сравнению с изменением температуры другой. Далее, поскольку , то второе условие соответствует случаю, когда средний температурный напор значительно превышает изменения температур рабочих жидкостей. Во всех остальных случаях при одной и той же поверхности нагрева и одинаковых крайних температурах теплоносителей при прямотоке передается меньше тепла, чем при противотоке. Поэтому с теплотехнической точки зрения всегда следует отдавать предпочтение противотоку, если какие-либо другие причины (например, конструктивные) не заставляют применять прямоток. При этом следует иметь в виду, что при противотоке создаются более тяжелые температурные условия для металла, ибо одни и те же участки стенок теплообменника с обеих сторон омываются рабочими жидкостями с наиболее высокой температурой.

При конденсации и кипении температура жидкости постоянна. Это означает, что водяной эквивалент такой жидкости бесконечно велик. В этом случае прямоток и противоток равнозначны, и уравнения (2.23) и (2.26) становятся тождественными. Конечная температура той жидкости, для которой водяной эквивалент имеет конечное значение, определяется следующим образом.

При конденсации паров;

(2.30)

и

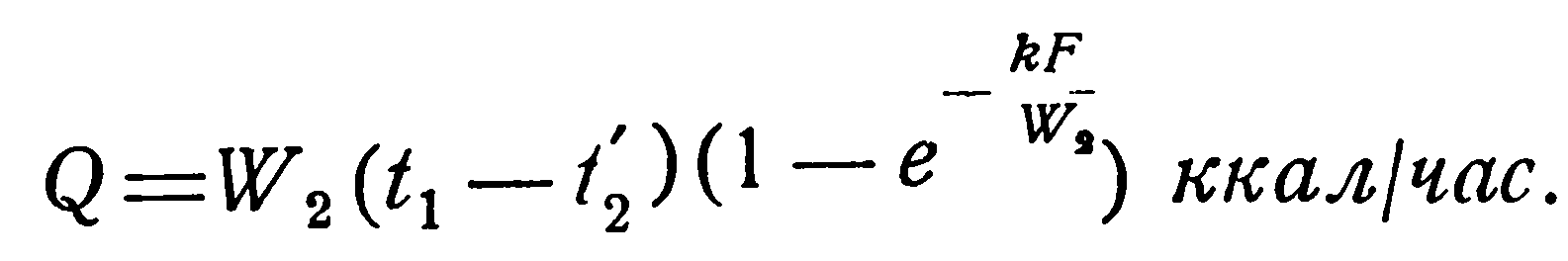(2.31)

При кипении жидкостей:

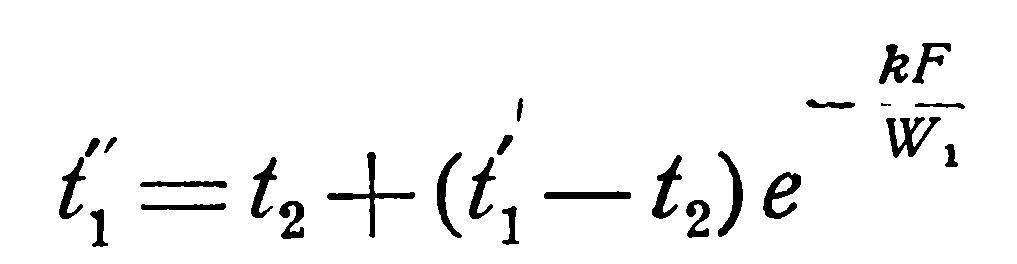(2.32)

и

(2.33)

Вместо t₁ и t₂ в уравнения (2.30) – (2.33) можно подставить температуру стенки, значение которой при этом также постоянно. Значения функции 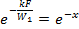находятся из таблиц показательных функций.

В случае перекрестного тока конечные температуры рабочих жидкостей находятся между конечными температурами для прямотока и противотока. Поэтому в приближенных расчетах можно пользоваться методом расчета одной из указанных схем. Если одна из жидкостей движется навстречу другой зигзагообразно (смешанный ток), то расчет может быть произведен, как для противотока.

4. Влияние тепловых потерь и проницаемости стенок.Все вышеприведенные формулы справедливы для случая, когда тепловые потери во внешнюю среду равны нулю. В действительности они всегда имеются. Более или менее точно учесть их влияние, вообще говоря, возможно, однако расчетные формулы при этом становятся громоздкими. Поэтому для учета влияния тепловых потерь в практике обычно применяется приближенный метод, который состоит в следующем.

Тепловые потери со стороны горячей жидкости вызывают более сильное падение ее .температуры. Это равносильно случаю, когда теплоотдающая жидкость в аппарате без потерь в окружающую среду имела бы меньшее значение водяного эквивалента. Поэтому влияние потерь в окружающую среду можно учесть, изменив водяной эквивалент теплоотдающей жидкости в тепловом аппарате таким образом, чтобы в последнем происходило такое же понижение температуры, как и при потоке с действительным водяным числом при наличии тепловых потерь. Внешние тепловые потери со стороны холодной жидкости оказывают обратное влияние, они уменьшают повышение температуры жидкости, что приводит к кажущемуся увеличению ее водяного эквивалента.

Наличие присоса наружного холодного воздуха оказывает такое же влияние, как и внешняя потеря тепла. Присосанный вездух на горячей стороне понижает температуру горячей жидкости (газа) точно так же, как если бы теплообменный аппарат был абсолютно непроницаем, но жидкость имела меньшее значение водяного эквивалента. Присос вездуха на холодной стороне понижает температуру холодной жидкости, что равносильно увеличению значения водяного эквивалента.

Если потеря тепла составляет р% к общему количеству передаваемого тепла, то вместо действительного значения водяного эквивалента W в расчетные формулы следует подставить значение W’ которое определяется следующим образом:

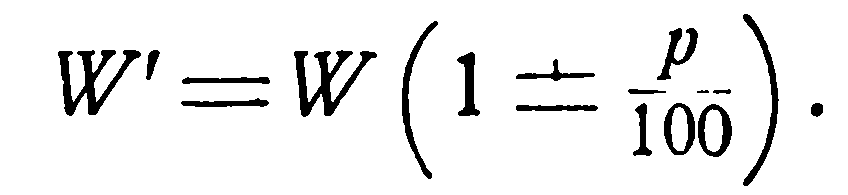(2.34)

Знак минус (-) берется для горячей, а знак плюс (+) для холодной жидкости.

При таком способе учета внешних тепловых потерь все приведенные выше формулы для расчета конечных температур можно применять без какого-либо их изменения.