Цифровое моделирование линейных узлов р/устройств

Моделирование линейных узлов возможно на основе:

1) ДУ;

2) Временного представления сигналов;

3) Спектрального представления сигналов;

4) Методов цифровой фильтрации.

Основные характеристики и свойства цифровых фильтров (ЦФ)

Предаточная функция цифрового фильтра: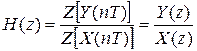

Импульсная характеристика равна

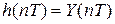при

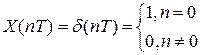
Импульсная характеристика 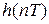и передаточная функция 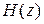связаны между собой парой Z-преобразований

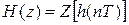
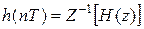
Уравнение, связывающее входные и выходные величины, для нерекурсивного фильтра имеет вид:

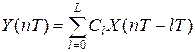(6)

Этой формуле соответствует схема

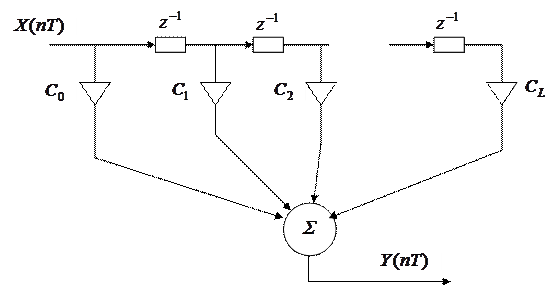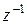- задержка на один такт моделирования.

Определим передаточную функцию нерекурсивного фильтра, взяв Z-преобразование для (6)

.

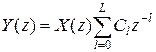
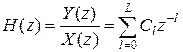Уравнение, связывающее входные и выходные величины для рекурсивного фильтра, имеет вид:

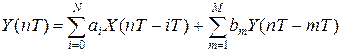(7)

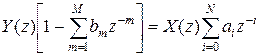
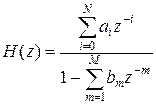
Передаточная функция 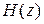нерекурсивного фильтра является многочленом переменной 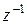, а передаточная функция рекурсивного фильтра – дробно-рациональной функцией переменной .

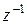Схема вычислений, соответствующая рекурсивному фильтру (2):

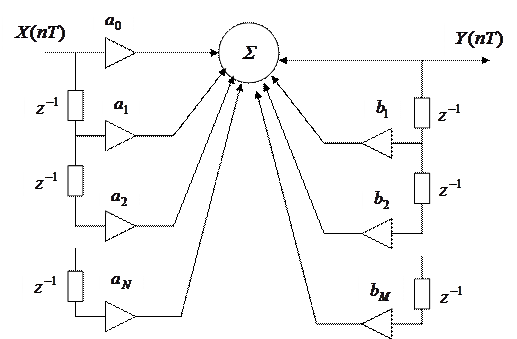Это – схема исходная или прямая.

Каноническая схема

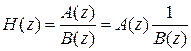
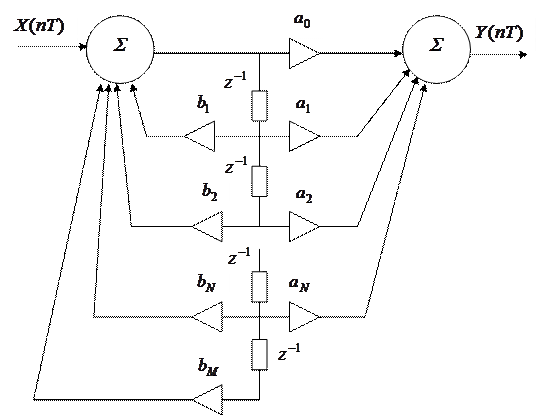По сравнению с прямой (или исходной) схемой число задержек на Т уменьшено.

Последовательная схема

Схема представляет собой последовательное соединение фильтров с передаточными функциями :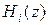

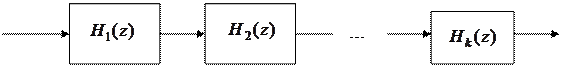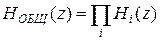
Передаточная функция 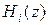может быть представлена в виде:

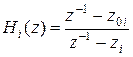
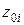- нуль числителя

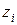- нуль знаменателя

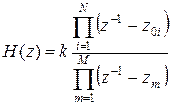
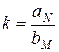
Чем выше порядок фильтра, тем меньше проигрыш последовательного фильтра по сравнению с каноническим.

Параллельная схема.

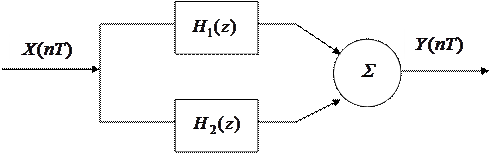По этой схеме вычисления входной сигнал поступает на вход фильтров 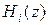, а выходные сигналы фильтров складываются.

Передаточная функция цифрового фильтра может быть записана:

.

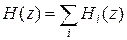Так же, как и последовательная схема, параллельная немного проигрывает канонической схеме вычислений. Чем выше порядок фильтра, тем меньше проигрыш.

По времени любая схема рекурсивного фильтра лучше, чем нерекурсивного. При помощи рекурсивного фильтра целесообразно моделировать узлы с импульсной характеристикой, протяженной во времени (например, фильтры высоких частот); при помощи нерекурсивного фильтра – моделировать узлы с быстрозатухающей или ограниченной во времени импульсной характеристикой (например, дифференцирующие устройства, низкочастотные фильтры, согласованные фильтры). Нерекурсивные фильтры, в силу того, что передаточная функция не имеет полюсов, а импульсная характеристика ограничена во времени, всегда устойчивы. Рекурсивные фильтры могут быть неустойчивы, причем, если моделируемое устройство является устойчивым, то полученная цифровая модель может быть неустойчивой (в частности, из-за неправильно выбранного метода построения модели).