Геометрические и физические задачи
Оглавление
1. Уравнения первого порядка. 4
1.1.Уравнения с разделяющимися переменными и уравнения, приводящиеся к ним 4
1.2. Геометрические и физические задачи. 5
Задание 1. 8
1.3. Однородные уравнения и уравнения, приводящиеся к ним. 10
Задание 2. 12
1.4. Линейные уравнения и уравнения Бернулли. 13
Задание 3. 15
1.5. Уравнения в полных дифференциалах. Интегрирующий множитель. 16
Задание 4. 19
1.6. Уравнения, не разрешенные относительно производной. Особые решения. 20
Задание 5. 23
1.7. Существование и единственность решения задачи Коши. 23
Метод последовательных приближений. 23
Задание 6. 25
2. Дифференциальные уравнения n-го порядка. 27
2.1. Методы интегрирования некоторых классов дифференциальных уравнений, допускающих понижение порядка. 27
Задание 7. 31
2.2. Линейные уравнения с постоянными коэффициентами. 32
Задание 8. 35
Задание 9. 36
Задание 10. 36
Задание 11. 51
3. Линейные системы с постоянными коэффициентами. 54
3.1 Матричная экспонента. 57
3.2. Формула Коши. 61
Задание 12. 61
Задание 13. 51
Задание 14. 61
Библиографический список. 51
Уравнения первого порядка
Уравнение вида
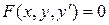(1.1)
(уравнение, неразрешенное относительно производной), или уравнение вида
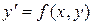(1.2)
(уравнение, разрешенное относительно производной), связывающее независимую переменную 
, искомую функцию 
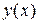и ее производную, называется дифференциальным уравнением первого порядка.
Задача отыскания решения уравнения (1.1) или (1.2), удовлетворяющего условию
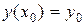, (1.3)
называется задачей Коши. Условие (1.3) – начальное условие.
Общим решением уравнения (1.1) или (1.2) называется функция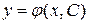 
такая, что
1) при любом значении постоянной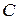 
эта функция является решение уравнения;
2) по начальным условиям (3) можно указать значение постоянной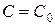 
так, что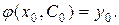 
Соотношение вида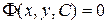 
, определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Решение, получающееся из общего, при конкретном значении произвольной постоянной – частное решение.
1.1.Уравнения с разделяющимися переменными и уравнения,
приводящиеся к ним
Пусть правая часть уравнения (1.2) может быть представлена в виде произведения двух функций, каждая из которых зависит только от одной переменной: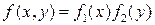 
, или пусть уравнение (1.1) имеет вид 
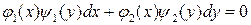. Тогда переменные в этих уравнения могут быть разделены, и мы получим следующие уравнения с разделенными переменными:
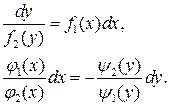
Общие интегралы этих уравнений имеют вид:
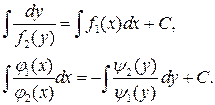
Замечание. При делении обеих частей уравнения на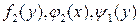 
могли быть потеряны решения, являющиеся нулями этих функций.
Пример 1. Решить уравнение
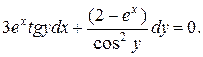
Решение. После разделения переменных получим
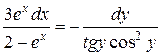. (1.4)
Интегрируя обе части полученного равенства, будем иметь
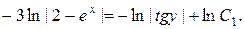
Здесь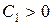 
– произвольное число. Таким образом, 
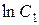– произвольная постоянная. Потенцируя, можем записать
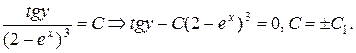
Найден общий интеграл уравнения.
При разделении переменных могли быть потеряны решения, обращающие в ноль знаменатели дробей в (1.4):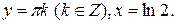 
Непосредственная подстановка в исходное уравнение показывает, что эти функции являются его решениями. Причем решения вида 
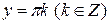могут быть получены из общего решения при 
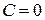, а решение 
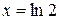должно быть добавлено к общему.
Уравнения вида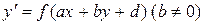 
сводятся к уравнению с разделяющимися переменными заменой 
.
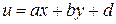Пример 2. Найти общее решение уравнения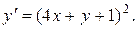 
Решение.Выполним замену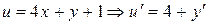 
. Уравнение примет вид 
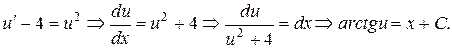Итак, общий интеграл уравнения имеет вид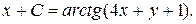 
Задание 2
Решить уравнение. Найти общее или частное решение.
1. 
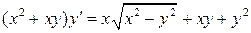
2. 
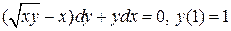
3. 
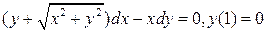
4. 
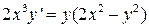
5. 
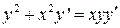
6. 
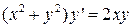
7. 
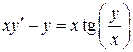
8. 
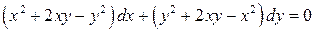
9. 
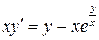
10. 
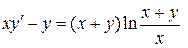
11. 
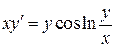
12. 
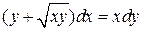
13. 
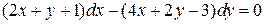
14. 
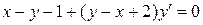
15. 
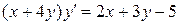
16. 
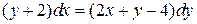
17. 
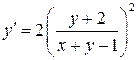
18. 
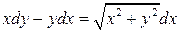
19. 
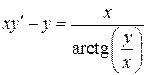
20. 
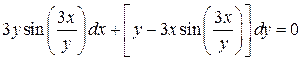
21. 
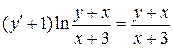
22. 
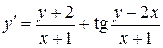
23. 
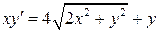
24. 
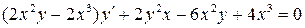
25. 
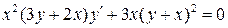
26. 
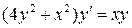
27. 
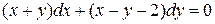
28. 
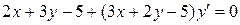
29. 
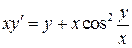
30. 
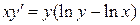
31. 
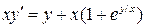
Задание 3
В задачах 1 -9 найти решения, удовлетворяющие заданным условиям
1. 
;
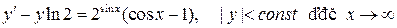2. 
;
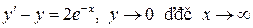3. 
;
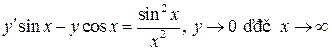4. 
;
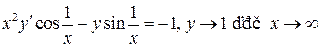5. 
;
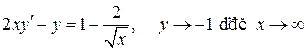6. 
;
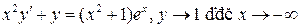7. 
;
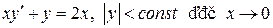8. 
;
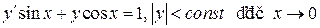9. 
.
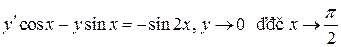Решить уравнения:
10. 
;
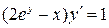11. 
;
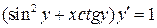12. 
;
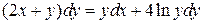13. 
;
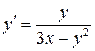14. 
;
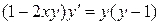15. 
;
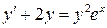16. 
;
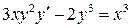17. 
;
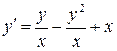18. 
;
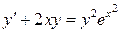19. 
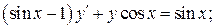
20. 
;
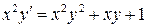21. 
;
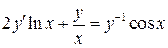22. 
;
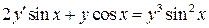23. 
;
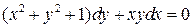24. 
;
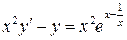25. 
;
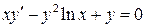26. 
;
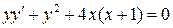27. 
;
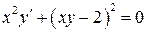28. 
;
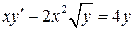29. 
;
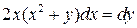30. 
;
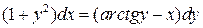31. 
.
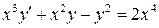Задание 4
Решить уравнения, убедившись предварительно, что они являются уравнениями в полных дифференциалах
1. 
2. 
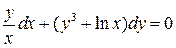
3. 
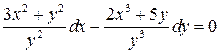
4. 
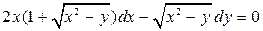
5. 
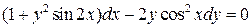
6. 
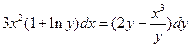
7. 
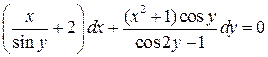
8. 
9. 
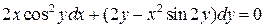
Решить уравнения, допускающие интегрирующий множитель вида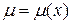 
или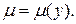 
10. 
11. 
12. 
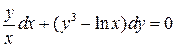
13. 
14. 
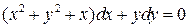
15. 
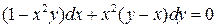
16. 
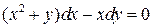
17.
18. 
19. 
20. 
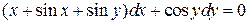
21. 
22. 
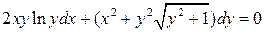
23. 
24. 
25. 
26. 
27. 
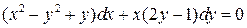
28. 
29. 
30. 
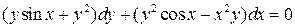
31. 
1.6. Уравнения, не разрешенные относительно производной.
Особые решения
Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид
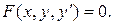(1.18)
Для решения уравнения (1.18) желательно разрешить его относительно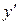 
. При этом может получиться несколько уравнений 
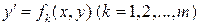, разрешенных относительно производной. Если удается найти решения всех этих уравнений, то, объединяя их, получим общее решение уравнения (1.18) .
Пример 1. Решить уравнение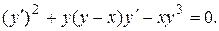 
Решение.Представим данное уравнение в виде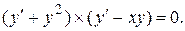 
Следовательно, данное уравнение эквивалентно совокупности двух уравнений: 
и 
Решения первого из них 
и 
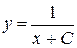. Решение второго 
Окончательно получаем, что общее решение исходного уравнения 
Однако уравнение (1.18) не всегда удается разрешить относительно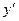 
. Часто разрешенное относительно 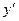уравнение плохо интегрируется. В некоторых случаях уравнение (1.18) удобнее интегрировать методом введения параметра.
Пусть, например, уравнение (1.18) легко разрешается относительно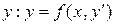 
. Введем параметр 
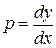. Тогда уравнение примет вид 
. Дифференцируя обе части последнего равенства по 
, получим 
. Если удается разрешить это уравнение относительно , то есть найти 
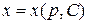, то получим решение исходного уравнения в параметрической форме:
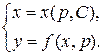
Пример 2.Решить уравнение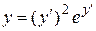 
.
Решение. Введем параметр 
Тогда
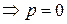или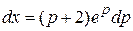 
.
Получаем, что 
или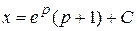 
. Значению соответствует решение .
Итак, решениями исходного уравнения являются и 
Пусть уравнение (1.18) может быть разрешено относительно х: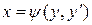 
. В этом случае уравнение может быть решено с использованием подстановки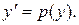 
Пример 3. Найти общее решение уравнения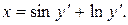 
Решение.
Итак, параметрические уравнения решения имеют вид
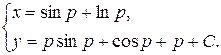
Как и уравнение, разрешенное относительно производной, уравнение (1.18) может иметь особые решения, то есть решения, целиком состоящие из особых точек (точек неединственности). Особые решения, если они имеются, удовлетворяют системе уравнений
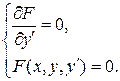(1.19)
Для каждой функции 
, удовлетворяющей системе (1.19), необходимо проверить, что она в самом деле является решением уравнения (1.18) и является особым решением, то есть в каждой точке кривой ее касаются другие интегральные кривые того же уравнения.
Особым решением дифференциального уравнения (1.18) будет являться и огибающая семейства 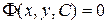интегральных кривых этого уравнения. Для нахождения огибающей семейства интегральных кривых 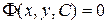следует исключить параметр 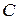из системы уравнений
(1.20)
и проверить, является ли полученная кривая огибающей, то есть, касаются ли ее в каждой точке кривые данного семейства.
Пример 4.Решить уравнение 
. Найти его особые решения (если они есть).
Решение.Положив 
, получим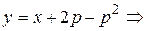 
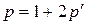
. То есть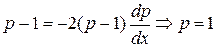 
или 
. Поэтому решениями исходного уравнения являются функции
и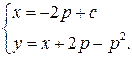 
Исключая параметр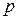 
, имеем 
.
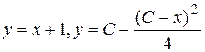Найдем теперь решения, "подозрительные" на особые. Система (1.19) в данном случае принимает вид
Исключая из нее 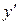, найдем: 
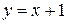. Проверим, является ли решение 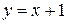особым, то есть проверим касаются ли его кривые семейства решений 
. Условия касания кривых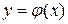 
и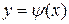 
в точке с абсциссой 
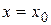выглядят так: 
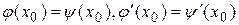. В данном случае они примут вид
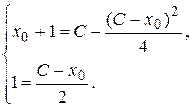
Исключая 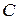из этой системы, получаем 
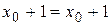. Это равенство справедливо при всех 
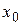. Последнее и означает, что 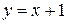– особое решение.
Заметим, что это же особое решение могло быть найдено из системы (1.20), которая в данном случае имеет вид
Задание 5
Найти все решения данных уравнений. Выделить особые решения (если они есть).
1. 
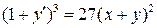
2. 
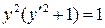
3. 
4. 
5. 
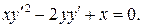
6. 
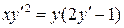
7. 
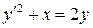
8. 
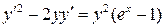
9. 
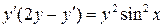
10. 
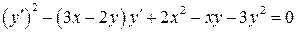
11. 
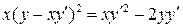
12. 
13. 
Уравнения 13-30 решить методом введения параметра. Найти особые решения (если они есть).
14. 
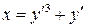
15. 
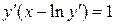
16. 
17. 
18. 
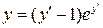
19. 
20. 
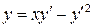
21. 
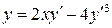
22. 
23. 
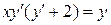
24. 
25. 
26. 
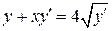
27. 
28. 
29. 
30. 
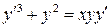
31. 
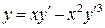
1.7. Существование и единственность решения задачи Коши.
Метод последовательных приближений
Укажем условия существования и единственности решения задачи Коши (1.2) – (1.3).
Теорема Пикара-Линделефа. Пусть функция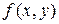 
непрерывна на множестве 
и удовлетворяет условию Липшица по 
равномерно относительно , то есть существует такая постоянная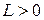 
, что для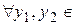 
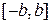и 
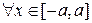выполнено соотношение
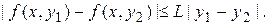
Пусть М является верхней границей для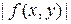 
на 
, а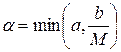 
. Тогда задача Коши
имеет на отрезке 
единственное решение.
Решение 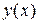задачи Коши при выполнении условий теоремы Пикара-Линделефа может быть найдено как предел при 
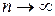равномерно сходящейся последовательности функций 
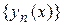, определяемых рекуррентными соотношениями
(1.21)
Оценка погрешности при замене точного решения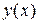 
-ым приближением 
может быть выражена неравенством
(1.22)
Заметим, что если функция 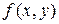имеет непрерывную частную производную 
в области , то значение постоянной Липшица L может быть определено так: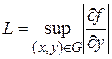 
.
Пример 1. Найти область, в которой уравнение 
имеет единственное решение.
Решение. Здесь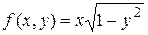 
. Функция 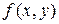определена и непрерывна при 
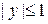. Частная производная 
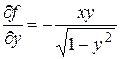непрерывна и ограничена при 
. Следовательно, данное уравнение имеет единственное решение в любой полосе 
Пример 2. Для задачи Коши 
указать какой-либо интервал существования решения. Найти это решение методом последовательных приближений, ограничившись приближениями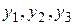 
и оценить ошибку третьего приближения.
Решение. Рассмотрим прямоугольник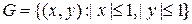 
. На множестве 
. Поэтому интервал существования решения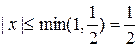 
. Значит, решение существует при 
и на этом же интервале сходятся последовательные приближения. Последовательные приближения найдем по формуле (1.21):
Оценим теперь ошибку третьего приближения, пользуясь формулой (1.22). В качестве значения постоянной L можно взять верхнюю границу для на G: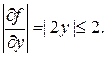 
Поэтому 
.
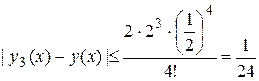Задание 6
Указать какой-нибудь отрезок, на котором существует решение с данными начальными условиями:
1. 
;
2. 
;
3. 
.
Построить последовательные приближения 
к решению данного уравнения с данными начальными условиями, указать какой-либо интервал, на котором сходится последовательность приближений:
4. 
5. 
6. 
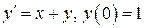
7. 
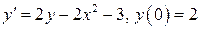
8. 
9. 
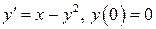
10. 
11. 
12. 
13. 
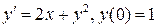
14. 
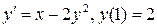
15. 
16. 
17. 
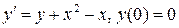
18. 
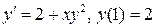
19. 
20. 
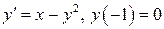
21. 
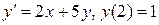
Для следующих уравнений построить третье приближение в заданной области (или на заданном интервале) и оценить его ошибку.
22. 
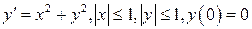
23. 
Для следующих уравнений выделить области на плоскости (x,y),в которых через каждую точку проходит единственное решение уравнения.
24. 
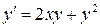
25. 
26. 
27. 
28. 
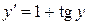
29. 
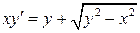
30. 
31. 
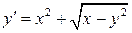
2. Дифференциальные уравнения n-го порядка
Дифференциальное уравнение вида
называется дифференциальным уравнением -го порядка не разрешенным относительно старшей производной. Если удается разрешить его относительно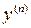 
, то получаем
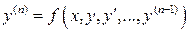. (2.1)
Теорема Коши(существования и единственности решения). Пусть функция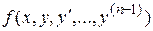 
, рассматриваемая как функция 
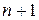переменной, непрерывна в некоторой области 
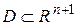, содержащей точку 
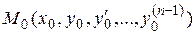, вместе со своими частными производными 
. Тогда существует интервал 
и определенная на нем n раз дифференцируемая функция 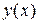, удовлетворяющая уравнению (2.1) и начальным условиям
. (2.2)
Функция 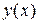, обладающая указанными свойствами, единственна.
Определение.Общим решением уравнения (2.1) (удовлетворяющего условиям теоремы Коши) называется функция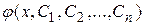 
, зависящая от x и n произвольных постоянных 
, такая, что
1) для любых значений произвольных постоянных функция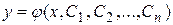 
есть решение уравнения (2.1);
2) существуют единственные значения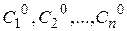 
такие, что 
есть решение уравнения (2.1), удовлетворяющее начальному условию (2.2).
Если общее решение в области 
задано неявно соотношением
,
то оно называется общим интегралом уравнения.
Любое решение, получающееся из общего при конкретных значениях произвольных постоянных , называется частным решением.
Задание 7
Решить дифференциальные уравнения, используя методы понижения порядка. Найти общее или (если заданы начальные условия) частное решение.
1. 
2. 
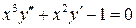
3. 
4. 
5. 
6. 
7. 
8. 
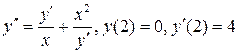
9. 
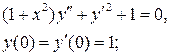
10. 
11. 
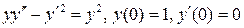
12. 
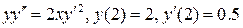
13. 
14. 
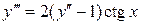
15. 
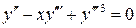
16. 
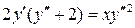
17. 
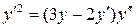
18. 
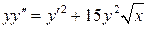
19. 
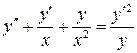
20. 
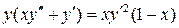
21. 
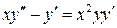
22. 
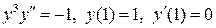
23. 
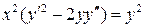
24. 
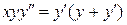
25. 
26. 
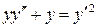
27. 
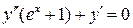
28. 
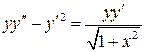
29. 
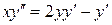
30. 
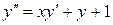
31. 
Задание 8
Найти общее решение дифференциального уравнения
1. 
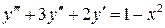
2. 
3. 
4. 
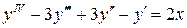
5. 
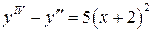
6. 
7. 
8. 
9. 
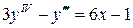
10. 
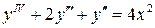
11. 
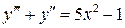
12. 
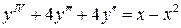
13. 
14. 
15. 
16. 
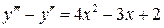
17. 
18. 
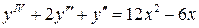
19. 
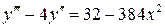
20. 
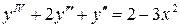
21. 
22. 
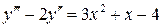
23. 
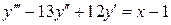
24. 
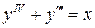
25. 
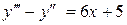
26. 
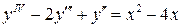
27. 
28. 
29. 
30. 
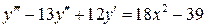
31. 
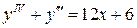
Задание 9
Найти общее решение дифференциального уравнения
1. 
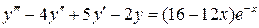
2. 
3. 
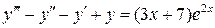
4. 
5. 
6. 
7. 
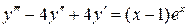
8. 
9. 
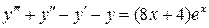
10. 
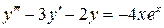
11. 
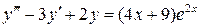
12. 
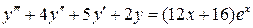
13. 
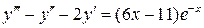
14. 
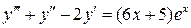
15. 
16. 
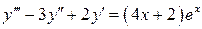
17. 
18. 
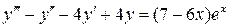
19. 
20. 
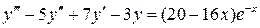
21. 
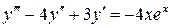
22. 
23. 
24. 
25. 
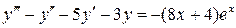
26. 
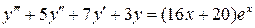
27. 
28. 
29. 
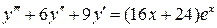
30. 
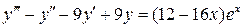
31. 
Задание 10
Найти общее решение дифференциального уравнения
1. 
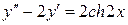
2. 
3. 
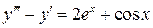
4. 
5. 
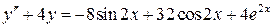
6. 
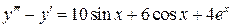
7. 
8. 
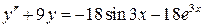
9. 
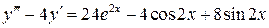
10. 
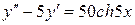
11. 
12. 
13. 
14. 
15. 
16. 
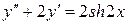
17. 
18. 
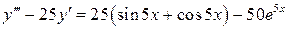
19. 
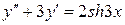
20. 
21. 
22. 
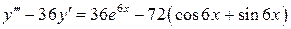
23. 
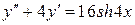
24. 
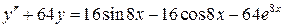
25. 
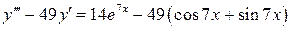
26. 
27. 
28. 
29. 
30. 
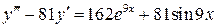
31. 
Задание 11
Найти решение задачи Коши
1. 
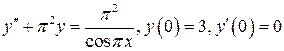
2. 
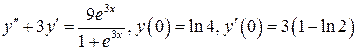
3. 
4. 
5. 
6. 
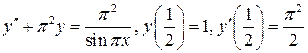
7. 
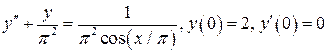
8. 
9. 
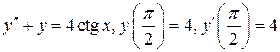
10. 
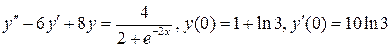
11.