Тема 6. Элементы операционного исчисления.

1.Знать определения оригинала и изображения. Изображения некоторых функций.

2.Используя таблицу основных формул соответствия и теоремы операционного исчисления, уметь находить изображения оригиналов и оригиналы по их изображениям.

3.Уметь находить изображения дифференциального выражения.

4.Уметь находить операционным методом частные решения дифференциальных уравнений с постоянными коэффициентами.

Задания для самостоятельного выполнения

1 Найти изображение F(p) по заданному оригиналу f(t):

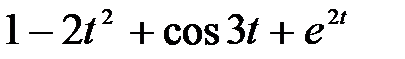а) ; б) ; в) .

2 Найти оригинал f(t) по изображению F(p):

а) ; б) ;

в) .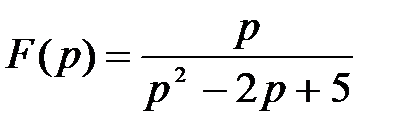

3 Найти изображение дифференциального выражения:

а) ;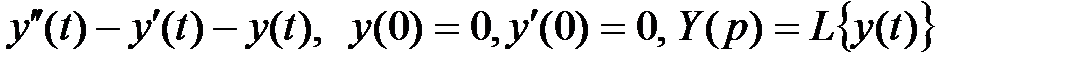

б) ;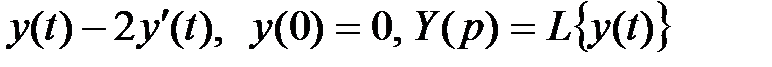

в) .

4Операционным методом найти решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.

а) 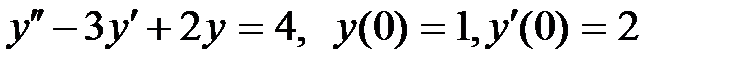; б) .

Образцы решения заданий

Любая комплексная функция f (t) действительного переменного t называется оригиналом, если она удовлетворяет следующим условиям:

1) f (t) – кусочно–непрерывная при t ≥ 0, это значит, что она либо непрерывна, либо в каждом конечном интервале имеет лишь конечное число точек разрыва 1-го рода;

2) f (t) ≡ 0 при t < 0;

3) при t → ∞ функция f (t) растёт не быстрее некоторой показательной функции (имеет ограниченную степень роста), т.е. существует такое положительное число М и такое неотрицательное число s, что для всех t ≥ 0 выполняется неравенство:| f (t) | ≤ M∙e^st, М > 0, s ≥ 0.

Точная нижняя грань s тех значений s, для которых выполняется указанное условие, называется показателем роста функции f(t).

Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного p=s+i из некоторой области D плоскости комплексного переменного p, определяемая равенством

F(p)= .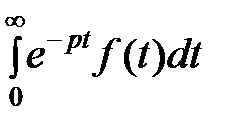

Связь между функциями f(t)и F(p) будем обозначать в дальнейшем следующим образом: f(t) = L^–1{F(p)} или F(p) = L{f(t)}.

Первую запись следует читать так: «Оригинал f (t) имеет изображение F (p)». Вторую запись следует читать так: «Изображение F (p) имеет оригинал f (t)» или «f (t) является оригиналом изображения F (p)». Используются также и другие обозначения.

Свойства преобразования Лапласа

1 Теорема единственности.Если два изображения F (р) и Φ (р) совпадают, то совпадают между собой и соответствующие им оригиналы во всех точках, за исключением, быть может, точек разрыва. То есть, если

F (p) = L{f(t)}, Ф (p) = L{φ (t)} и F (p) ≡ Ф (p), то f (t) ≡ φ (t)

во всех точках непрерывности f (t).

2 Теорема линейности. Если f (t) = L^–1{F (p)}, g (t) = L^–1{G (p)} для любых действительных или комплексных постоянных с₁ и с₂

с₁f (t) + с₂g (t) = с₁ L^–1{F (p)} + с₂ L^–1{G (p)}, Re p > s₀^(k) (k = 1,2,)

т.е. линейной комбинации оригиналов соответствует такая же линейная комбинация изображений.

3. Теорема подобия. Если f (t) = L^–1{F (p)}, Re p > s₀, то для любого числа а > 0

f (аt) = 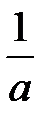L^–1{ 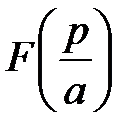}, Re p > аs₀,

т.е. умножение аргумента оригинала на положительное число приводит к делению аргумента изображения и самого изображения на то же число а.

4. Теорема запаздывания.Если f (t) = L^–1{F (p)}, Re p > s₀, то для любого положительного числа τ

f (t – τ) = e^{– рτ} L^–1{F (p)}, Re p > s₀.

5. Теорема о смещении изображения (затухания).Если

f (t) = L^–1{F (p)}, Re p > s₀, то для любого действительного или комплексного числа α

e^αtf (t) = L^–1{F(р – α)}, Re (р – α) > s_0,

т.е. умножение оригинала на функцию e^αt, влечёт за собой «смещение» переменной p.

6. Теорема дифференцирования оригинала. Если функции f(t), f (t), … , f (t) являются функциями-оригиналами, то

f ^/ (t) = p L^–1{F (p)} – f (0),

f ^// (t) = p 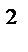L^–1{F (p)}-p f (0) – f ^/ (0),

…

f (t) = p L^–1{F (p)} – p f(0) – p 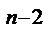f ^/ (0)-…-f (0).

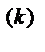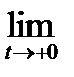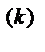Величина f (0), k=0, 1, … , n-1, понимается как f (t).

7. Теорема об интегрировании оригинала.Если функция f (t) является оригиналом и f (t) = L^–1{F (p)} то функция g(t) = 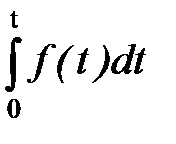также является оригиналом и g(t) = 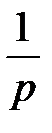L^–1{F (p)}

т.е. интегрирование оригинала в пределах от 0 до t приводит к делению изображения на p.

На основании определений оригинала и изображения и основных свойств преобразований Лапласа можно составить таблицу основных формул соответствия (таблица 6. 1).

Таблица 6. 1 – Таблица основных формул соответствия

Номер формулы	Оригинал	Изображение
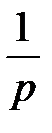	eαt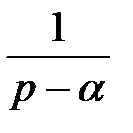
	sin ωt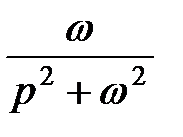
	cos ωt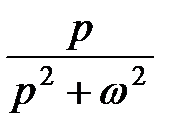
	sh ωt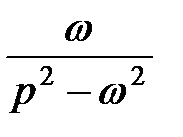
	ch ωt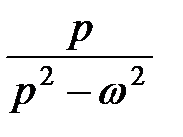
	t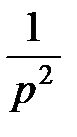
	tn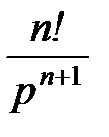
	tn∙eαt
	t∙sin ωt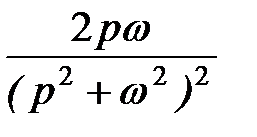
	t∙cos ωt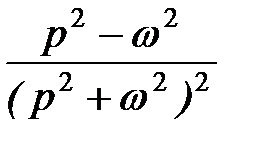

Задание 1 .Найти изображение функции , используя основные свойства (теоремы) преобразования Лапласа.

Решение. Найдем изображение каждого из слагаемых функции . Из таблиц соответствия известно, что:

1 = L^–1{ }.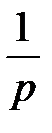

По теореме об интегрировании оригинала имеем

.

Так как , то . Тогда по теореме о смещении изображения (затухания) получим

.

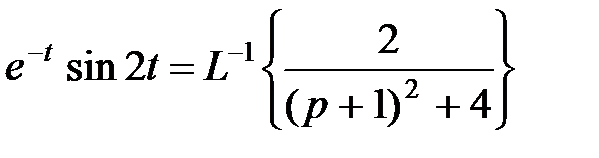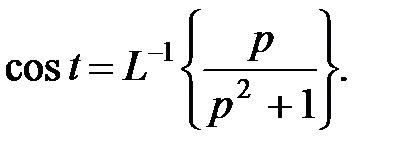
Применяя теорему подобия, находим

.

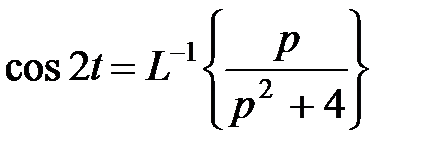Для нахождения изображения функции применим теорему о дифференцировании изображения. Получим

.

Далее, применяя теорему линейности преобразования Лапласа, получим

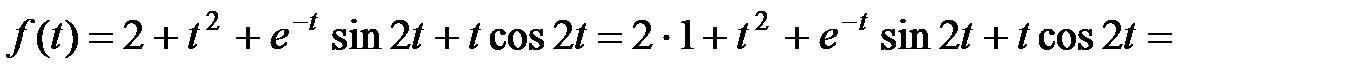
= 2 L^–1{ } + + + .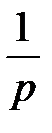

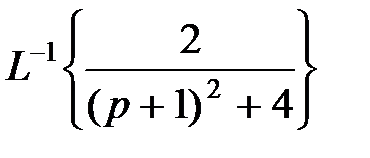Следовательно,

.

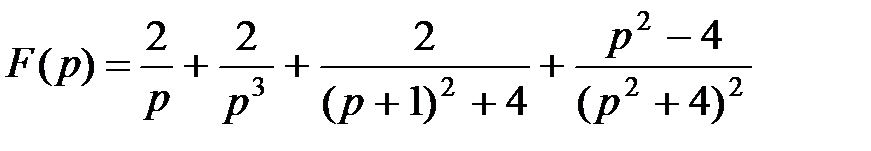Задание 2.Найти оригинал f(t) по изображению .

Решение.Используя табличные операционные соотношения и свойства линейности, получаем .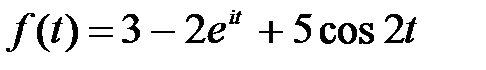

Задание 3.Найти изображение дифференциального выражения 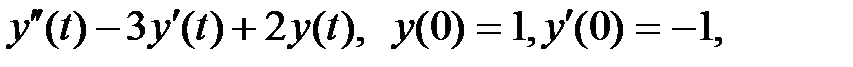y (t) = L^–1{Y (p)}

Решение.На основании свойства дифференцирования оригинала получаем:

= p L^–1{Y (p)} – y (0),

Используя свойство линейности, находим

,
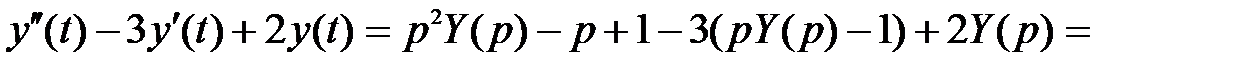
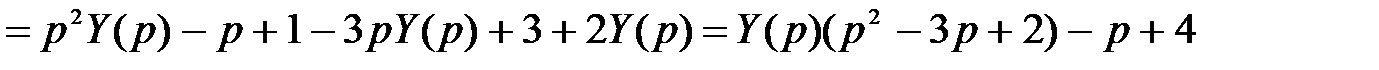