Тема 3. Числовые и функциональные ряды.
1. Находить члены числовых рядов.
2. Определять, какой ряд является знакопеременным, знакочередующимся, гармоническим, обобщенным гармоническим.
3. Знать определение сходящегося ряда.
4. Знать и уметь применять необходимый признак сходимости ряда.
5. Знать и уметь применять достаточные признаки сходимости положительных рядов: признаки сравнения, признак Даламбера, признак Коши, интегральный признак сходимости.
6. Знать и уметь применять признак Лейбница сходимости знакочередующегося ряда.
7. Определять коэффициенты степенного ряда.
8. Находить радиус сходимости степенного ряда.
9. Находить интервал сходимости степенного ряда.
10. Находить область сходимости степенного ряда.
11. Знать определение ряда Тейлора, ряда Маклорена.
Задания для самостоятельного выполнения.
1. Записать первые пять членов ряда по заданному общему члену:
а) 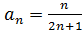 ;
;
б) 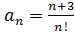 , где
, где 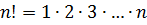 ;
;
в) 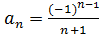 .
.
4. Исследовать сходимость ряда:
а) 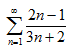 ; б)
; б) 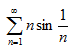
5. Исследовать сходимость ряда:
а) 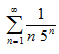 ; б)
; б) 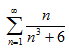 ; в)
; в) 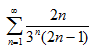 ; г)
; г) 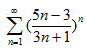 ; д)
; д) 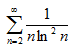 .
.
6. Исследовать на абсолютную или условную сходимость ряд:
а) 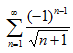 ; б)
; б) 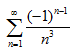 ; в)
; в) 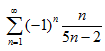 .
.
7. Определить коэффициенты степенного ряда:
а) 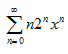 ; б)
; б) 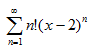 ; в)
; в) 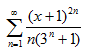 .
.
8. Найти радиус сходимости степенного ряда 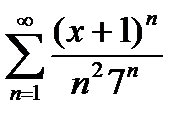 .
.
9. Найти интервал сходимости степенного ряда 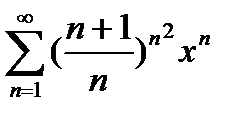 .
.
10. Найти область сходимости степенного ряда 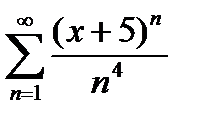 .
.
11. Найти первые четыре члена ряда Тейлора для функции 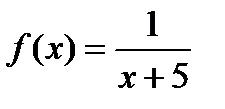 в окрестности точки
в окрестности точки 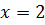 .
.
Образцы решения заданий.
Задание 1.Написать первые три члена ряда, общий член которого
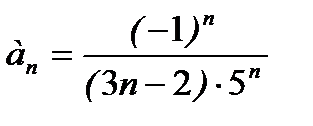
Решение.Полагая в данной формуле n=1,2,3, получаем:
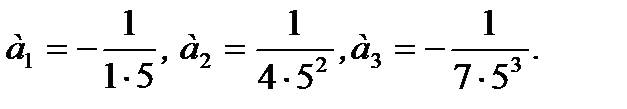
Задание 2.Найти формулу общего члена ряда
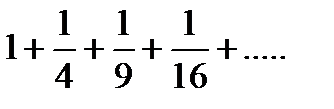
Решение.В рассматриваемом ряде члены представлены в виде дробей. Числитель каждой дроби – число 1, а знаменатель – квадрат натурального числа. Тогда 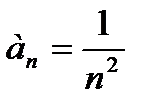 . Данный ряд можно записать также в виде
. Данный ряд можно записать также в виде 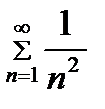 .
.
Задание 3.Исследовать ряд 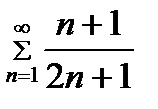 на сходимость.
на сходимость.
Решение.Заметим, что предел общего члена рассматриваемого ряда 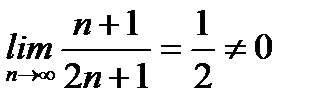 . Поэтому, согласно необходимому признаку сходимости, ряд
. Поэтому, согласно необходимому признаку сходимости, ряд 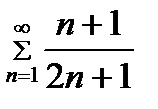 не может сходиться, т.е. он расходится.
не может сходиться, т.е. он расходится.
Задание 4.Исследовать на сходимость ряд
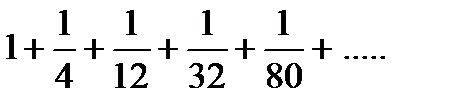
Решение. Заданный ряд запишем в виде 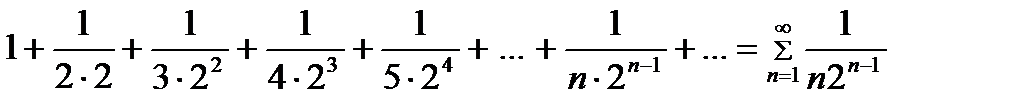 и сравним его с рядом
и сравним его с рядом 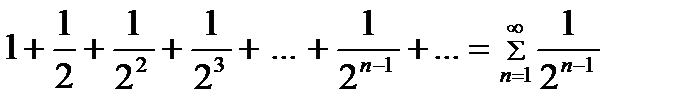 . Ряд
. Ряд 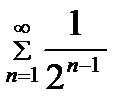 сходится, т.к. является геометрическим рядом со знаменателем
сходится, т.к. является геометрическим рядом со знаменателем 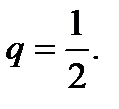 Кроме того,
Кроме того, 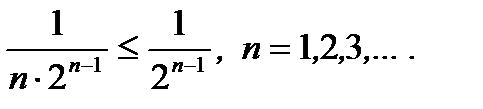 Значит, согласно признаку сравнения, ряд
Значит, согласно признаку сравнения, ряд 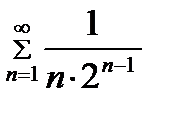 сходится.
сходится.
Задание 5.Исследовать на сходимость ряд 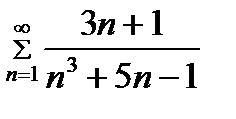 .
.
Решение.Возьмем для сравнения ряд 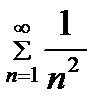 , который сходится как обобщенный гармонический ряд, у которого α = 2>1.
, который сходится как обобщенный гармонический ряд, у которого α = 2>1.
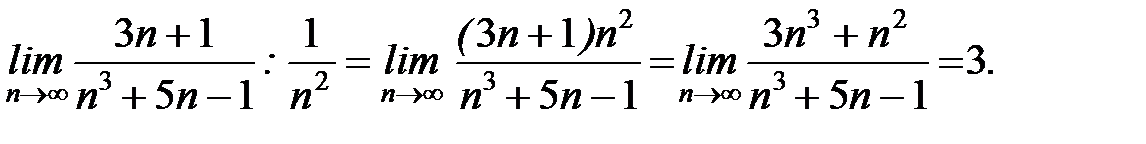 Значит, согласно предельному признаку сравнения, ряд
Значит, согласно предельному признаку сравнения, ряд 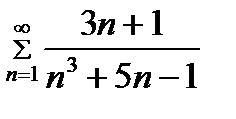 сходится.
сходится.
Задание 6.Исследовать на сходимость ряд 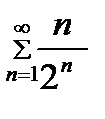 .
.
Решение. Запишем 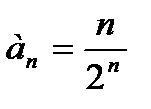 . Чтобы получить выражение для
. Чтобы получить выражение для 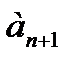 , необходимо в формулу n-го члена ряда подставить n+1 вместо n:
, необходимо в формулу n-го члена ряда подставить n+1 вместо n: 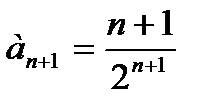 .
.
Имеем: 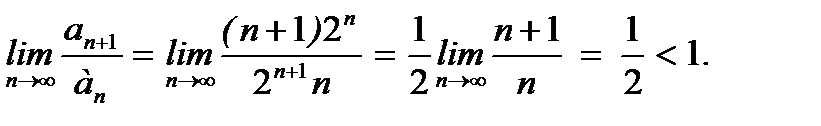
По признаку Д/Аламбера данный ряд сходится.
Задание 7. Исследовать на сходимость ряд 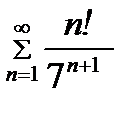 .
.
Решение. 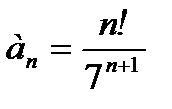 ,
, 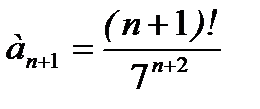
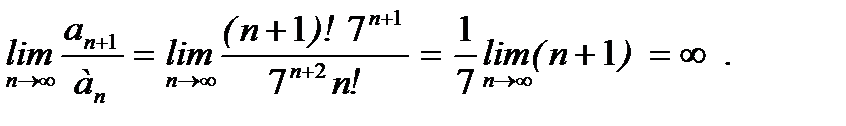 Данный ряд расходится.
Данный ряд расходится.
Задание 8.Исследовать на сходимость ряд 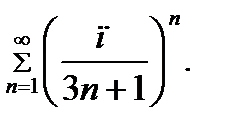
Решение. 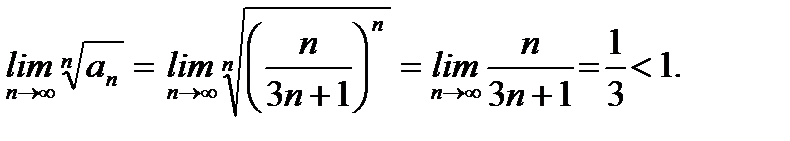
По признаку Коши ряд 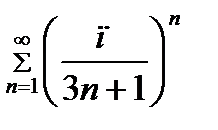 сходится.
сходится.
Задание 9. Исследовать на сходимость ряд 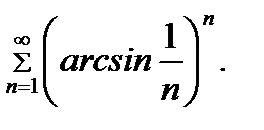
Решение. 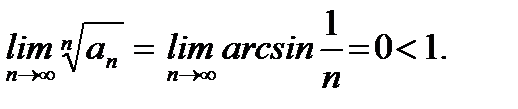 Данный ряд сходится.
Данный ряд сходится.
Задание 10.Исследовать на сходимость ряд 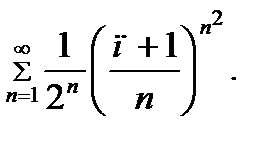
Решение. 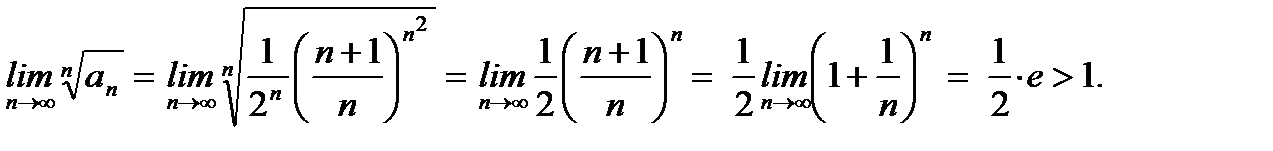
Согласно признаку Коши ряд 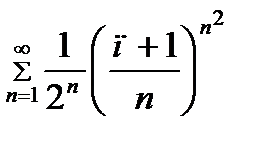 расходится.
расходится.
Задание 11. Исследовать на сходимость ряд 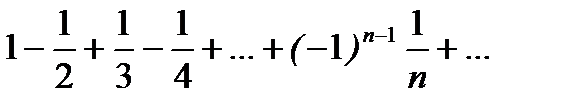
Решение. Данный ряд является знакочередующимся, исследуем его по признаку Лейбница:
а) 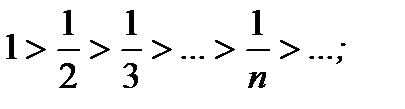 б)
б) 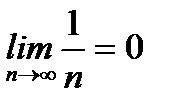 . Итак, данный ряд сходится.
. Итак, данный ряд сходится.
Задание 12. Выяснить вопрос об условной или абсолютной сходимости ряда 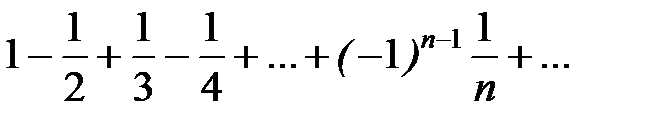 .
.
Решение. Ряд сходится условно, т.к. он сходится по признаку Лейбница, а ряд, составленный из его модулей 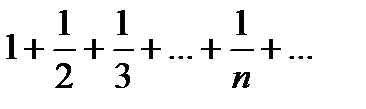 , расходится, ибо является гармоническим рядом.
, расходится, ибо является гармоническим рядом.
Задание 13.Найти радиус и интервал сходимости степенного ряда и исследовать сходимость ряда на концах интервала сходимости 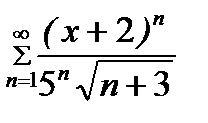 .
.
Решение. Для определения радиуса сходимости степенного ряда воспользуемся формулой: R = 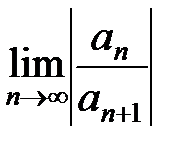 .
.
Так как ап = 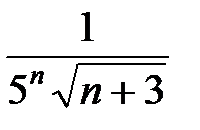 и ап + 1 =
и ап + 1 = 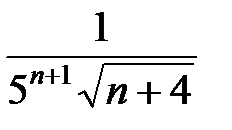 , то
, то
R = 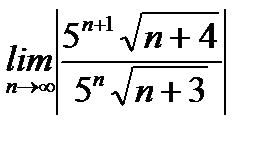 =5
=5 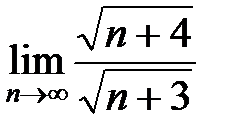 =5
=5 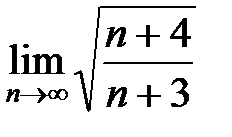 =5
=5 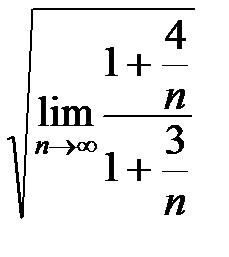 =5.
=5.
Итак, радиус сходимости ряда R = 5.
Определим интервал сходимости данного степенного ряда:
|x + 2| < 5  – 5< x + 2 < 5
– 5< x + 2 < 5  – 7 < x < 3.
– 7 < x < 3.
Итак, (– 7; 3) – интервал сходимости степенного ряда.
Исследуем сходимость ряда на концах интервала сходимости, то есть в точках х = – 7 и х = 3.
Пусть х = – 7. Подставим это значение в исследуемый степенной ряд. Получим знакочередующийся числовой ряд:
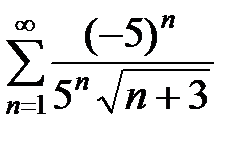 =
= 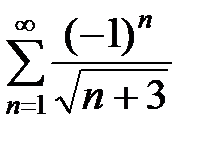 .
.
Так как 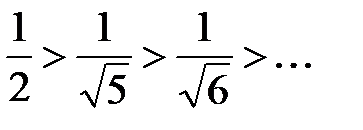 и
и 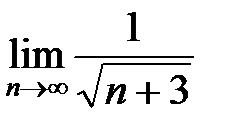 = 0, то согласно признаку Лейбница данный ряд сходится. Таким образом, х = – 7 принадлежит области сходимости степенного ряда.
= 0, то согласно признаку Лейбница данный ряд сходится. Таким образом, х = – 7 принадлежит области сходимости степенного ряда.
Пусть х = 3. Подставив это значение в исследуемый степенной ряд, получим числовой ряд с положительными членами:
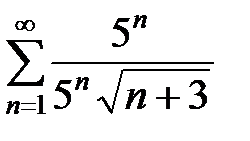 =
= 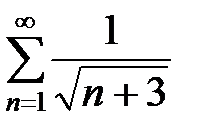 .
.
Сравним данный ряд с обобщенным гармоническим рядом 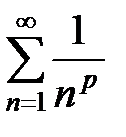 при р =
при р = 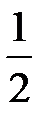 < 1, который является расходящимся. Для исследования на сходимость применим предельный признак сравнения. Получим
< 1, который является расходящимся. Для исследования на сходимость применим предельный признак сравнения. Получим
= 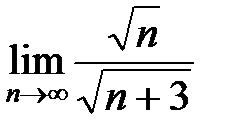 = 1 ≠ 0.
= 1 ≠ 0.
Следовательно, оба ряда ведут себя одинаково и исследуемый ряд, как и вспомогательный ряд, расходится. Таким образом, х = 3 не принадлежит области сходимости степенного ряда.
Поэтому, областью сходимости исследуемого степенного ряда является полуинтервал [– 7; 3).
Ответ: R = 5, [– 7; 3).
