Это так называемый биноминальный закон распределения
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Оглавление.
1. Дискретные случайные величины.
2. Часто встречающиеся распределения дискретной случайной величины.
3. Функция распределения вероятностей случайной величины и ее свойства.
4. Непрерывные случайные величины.
5. Равномерное распределение.
6. Нормальное распределение.
7. Экспоненциальное распределение.
8. Двумерные случайные величины.
Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, является число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д.
Таким образом, случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное числовое значение.
В дальнейшем мы рассмотрим два типа случайных величин — дискретные и непрерывные.
1. Дискретные случайные величины.
Рассмотрим случайную величину (случайные величины будем обозначать прописными буквами латинского алфавита: 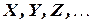 )
)  , возможные значения которой образуют конечную или бесконечную последовательность чисел
, возможные значения которой образуют конечную или бесконечную последовательность чисел 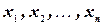 . Такая случайная величина
. Такая случайная величина  называется дискретной (прерывной).
называется дискретной (прерывной).
На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные. Поэтому
для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.
Важнейшей характеристикой случайной величины служит ее распределение вероятностей.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) или графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности:
 | 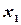 | 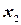 | … | 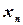 |
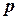 | 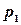 | 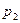 | … | 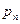 |
Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события 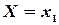 ,
, 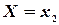 , …,
, …, 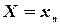 образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:
образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:
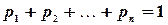 .
.
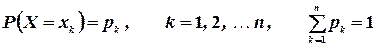 (3.1)
(3.1)
Эту таблицу называют рядом распределения случайной величины  . Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости. По горизонтальной оси будем откладывать возможные значения случайной величины
. Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости. По горизонтальной оси будем откладывать возможные значения случайной величины  , а по вертикальной оси - значения функции
, а по вертикальной оси - значения функции 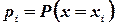 . График функции р(х) изображен на рис. 3.1. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.
. График функции р(х) изображен на рис. 3.1. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.
Пример 3.1. Пусть событие А — появление одного какого-либо очка при бросании игральной кости. Как мы знаем, вероятность выпадения какого-либо очка для всех цифр (1, 2, 3, 4, 5, 6) одинакова и равна Р(A)=1/6. Рассмотрим случайную величину  — число наступлений события А (т.е. число т) при десяти бросаниях игральной кости (т.е. n=10). Значения функции р(х) (закона распределения) приведены в следующей таблице:
— число наступлений события А (т.е. число т) при десяти бросаниях игральной кости (т.е. n=10). Значения функции р(х) (закона распределения) приведены в следующей таблице:
Значения  | … | ||||||||
Вероятности 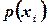 | 0,162 | 0,323 | 0,291 | 0,155 | 0,054 | 0,013 | 0,002 | … |
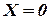 означает, что цифра 1 (или любая другая из шести, могущих выпасть) при десяти бросаний кости не выпала ни разу.
означает, что цифра 1 (или любая другая из шести, могущих выпасть) при десяти бросаний кости не выпала ни разу. 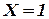 - цифра 1 при десяти бросаний выпала один раз.
- цифра 1 при десяти бросаний выпала один раз. 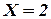 - два раза и т.д.
- два раза и т.д.
Вероятности 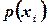 приведенные в таблице, вычислены по формуле Бернулли (
приведенные в таблице, вычислены по формуле Бернулли ( 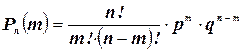 ) при n=10. Для x>6 они практически равны нулю:
) при n=10. Для x>6 они практически равны нулю:
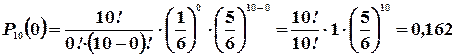
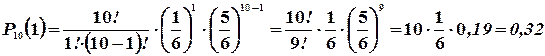
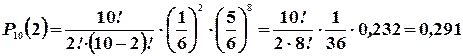
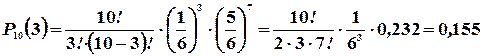
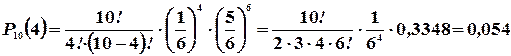
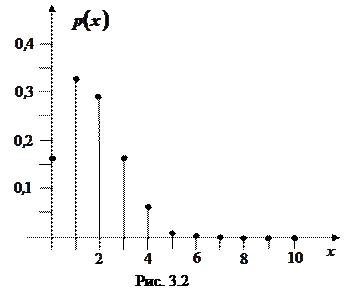
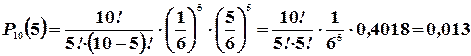
График функции p(x) изображен на рис. 3.2.
Замечание.
Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытаний конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания.
В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение  как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение
как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение  .
.
Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.
Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.
Пример 20. Плотность распределения непрерывной случайной величины задана следующим образом:
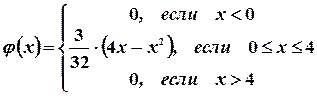
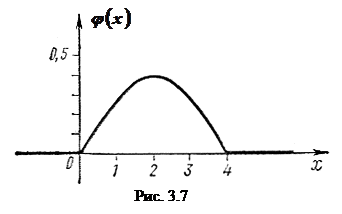 |
График функции
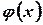 представлен па рис. 3.7.
представлен па рис. 3.7.
|
 примет значение, удовлетворяющее неравенствам
примет значение, удовлетворяющее неравенствам 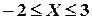 . 2) Найти функцию распределения заданной случайной величины.
. 2) Найти функцию распределения заданной случайной величины. Решение: Используя формулу (3.6), имеем:
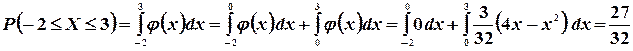
По формуле (3.6) находим функцию распределения F(x) для заданной случайной величины. Если 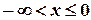 , то
, то 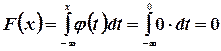 .
.
Если 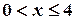 , то
, то
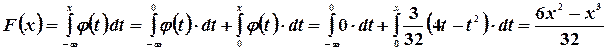 Если
Если 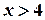 , то
, то
ч 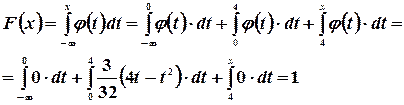
Итак,
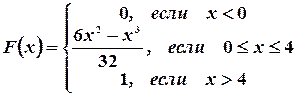
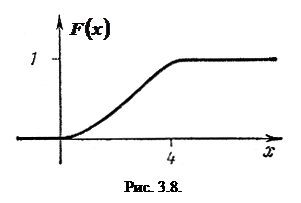
График функции F(x) изображен на рис. 3.8.
 |
Следующие три пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному, экспоненциальному и нормальному распределениям.
5. Равномерное распределение.
Пусть сегмент 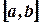 на оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина
на оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина  могущая принять любое значение из сегмента
могущая принять любое значение из сегмента 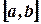 . Поэтому
. Поэтому 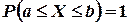 . Если, далее,
. Если, далее, 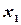 и
и 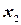
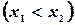 - две любые отметки на шкале, то согласно условию имеем
- две любые отметки на шкале, то согласно условию имеем 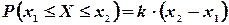 , где k - коэффициент пропорциональности, не зависящий от
, где k - коэффициент пропорциональности, не зависящий от 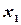 и
и 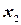 , а разность
, а разность 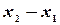 , - длина сегмента
, - длина сегмента 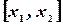 . Так как при
. Так как при 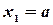 и
и 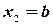 имеем
имеем 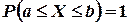 , то
, то 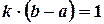 , откуда
, откуда 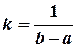 . Таким образом
. Таким образом
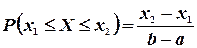 (3.9)
(3.9)
Теперь легко найти функцию F(x) распределения вероятностей случайной величины  . Если
. Если 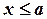 , то
, то 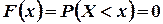 так как
так как  не принимает значений, меньших a. Пусть теперь
не принимает значений, меньших a. Пусть теперь 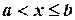 . По аксиоме сложения вероятностей
. По аксиоме сложения вероятностей 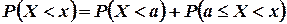 . Согласно формуле (3.9), в которой принимаем
. Согласно формуле (3.9), в которой принимаем 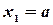 и
и 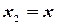 , имеем
, имеем 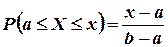 . Так как
. Так как 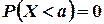 , то при
, то при 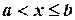 получаем
получаем 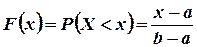 . Наконец, если
. Наконец, если 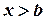 , то
, то 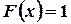 , так как значения
, так как значения  лежат на сегменте
лежат на сегменте 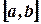 и, следовательно, не превосходят b. Итак, приходим к следующей функции распределения:
и, следовательно, не превосходят b. Итак, приходим к следующей функции распределения:
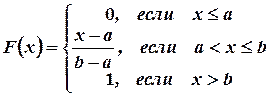 .
.
График функции F(x) представлен на рис. 3.9.
Плотность распределения вероятностей найдем по формуле (3.8). Если 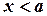 или
или 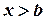 , то
, то 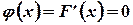 . Если
. Если 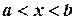 , то
, то
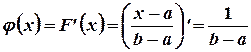 .
.
Таким образом,
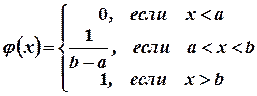 (3.10)
(3.10)
График функции 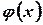 изображен на рис. 3.10. Заметим, что в точках aи b функция
изображен на рис. 3.10. Заметим, что в точках aи b функция 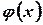 терпит разрыв.
терпит разрыв.
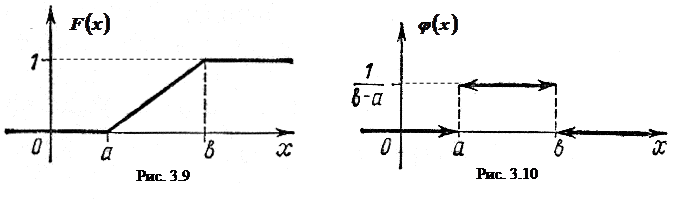
Величина, плотность распределения которой задана формулой (3.10), называется равномерно распределенной случайной величиной.
Нормальное распределение.
Говорят, что случайная величина  нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения
нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения 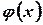 имеет вид
имеет вид
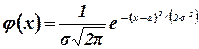 (3.11)
(3.11)
где 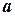 - любое действительное число, а
- любое действительное число, а 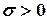 . Смысл параметров
. Смысл параметров 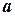 и
и 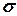 будет установлен в дальнейшем. Исходя из связи между плотностью распределения
будет установлен в дальнейшем. Исходя из связи между плотностью распределения 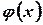 и функцией распределения F(x) [см. формулы (3.5, 3.8)], имеем
и функцией распределения F(x) [см. формулы (3.5, 3.8)], имеем
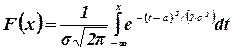
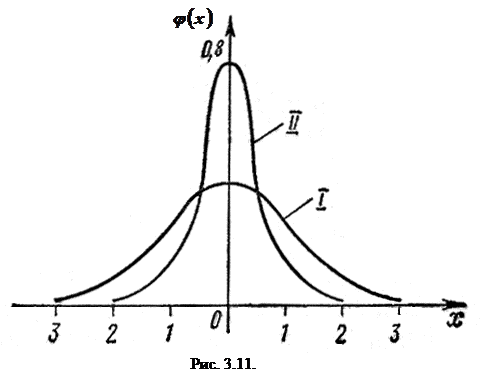 |
График функции
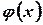 симметричен относительно прямой
симметричен относительно прямой 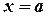 . Несложные исследования показывают, что функция
. Несложные исследования показывают, что функция 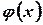 достигает максимума при
достигает максимума при 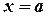 , а ее график имеет точки перегиба при
, а ее график имеет точки перегиба при  и
и 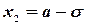 . При
. При 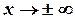 график функции асимптотически приближается к оси Ox. Можно показать, что при увеличении
график функции асимптотически приближается к оси Ox. Можно показать, что при увеличении 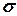 кривая плотности распределения становится более пологой. Наоборот, при уменьшении
кривая плотности распределения становится более пологой. Наоборот, при уменьшении 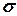 график плотности распределения сжимается к оси симметрии. При
график плотности распределения сжимается к оси симметрии. При 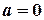 осью симметрии является ось Oy. На рис. 3.11 изображены два графика функции
осью симметрии является ось Oy. На рис. 3.11 изображены два графика функции 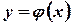 . График I соответствует значениям
. График I соответствует значениям 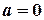 ,
,  , а график II - значениям
, а график II - значениям 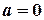 ,
, 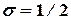 .
. Покажем, что функция 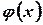 удовлетворяет условию (3.7), т.е. при любых
удовлетворяет условию (3.7), т.е. при любых 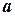 и
и 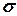 выполняется соотношение
выполняется соотношение
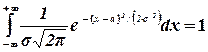
В самом деле, сделаем в этом интеграле замену переменной, полагая 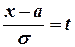 . Тогда
. Тогда
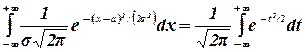
В силу четности подынтегральной функции имеем
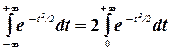 .
.
Следовательно,
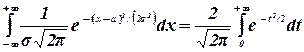
Но, 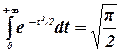 .
.
В результате получим
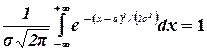 (3.12)
(3.12)
Найдем вероятность  . По формуле (3.6) имеем
. По формуле (3.6) имеем
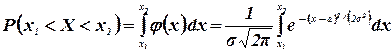
Сделаем в этом интеграле замену переменной, снова полагая 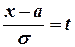 . Тогда
. Тогда 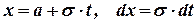 , и
, и
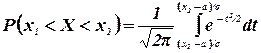 (3.13)
(3.13)
Как мы знаем, интеграл 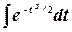 не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (3.13) вводится функция, которую мы определяли раньше [формула (2.9)] :
не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (3.13) вводится функция, которую мы определяли раньше [формула (2.9)] :
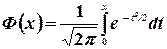 (3.14)
(3.14)
называемая интегралом вероятностей.
Для этой функции составлены таблицы ее значений для различных значений аргумента (см. табл. II Приложения). Используя формулу (3.13) получим:
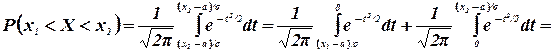
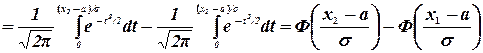
Итак,
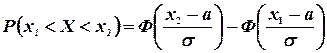 (3.15)
(3.15)
Легко показать, что функция Ф(х)(интеграл вероятностей) обладает следующими свойствами.
1°. Ф(0)=0
2°. 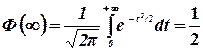 ;
;
при 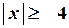 величина
величина 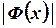 практически равна 1/2 (см. табл. II).
практически равна 1/2 (см. табл. II).
3°. 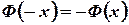 ,
,
т.е. интеграл вероятностей является нечетной функцией.
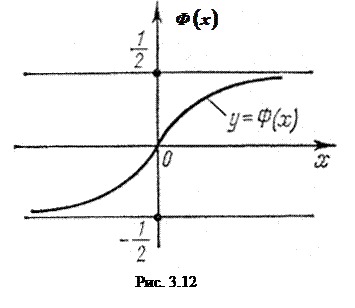
График функции Ф(х) изображен на рис. 3.12.
 |
Таким образом, если случайная величина
 нормально распределена с параметрами a и
нормально распределена с параметрами a и 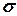 , то вероятность того, что случайная величина удовлетворяет неравенствам
, то вероятность того, что случайная величина удовлетворяет неравенствам 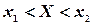 , определяется соотношением (3.15).
, определяется соотношением (3.15). Пусть  . Найдем вероятность того, что нормально распределенная случайная величина
. Найдем вероятность того, что нормально распределенная случайная величина  отклонится от параметра a по абсолютной величине не более чем на
отклонится от параметра a по абсолютной величине не более чем на 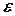 , т.е. рассмотрим неравенство -
, т.е. рассмотрим неравенство - 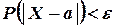 .
.
Так как неравенство  равносильно неравенствам
равносильно неравенствам 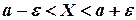 , то полагая в соотношении (3.15)
, то полагая в соотношении (3.15) 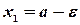 ,
, 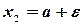 получим
получим
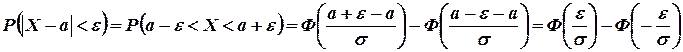
Вследствие того, что интеграл вероятностей - нечетная функция, имеем
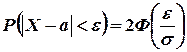 (3.16)
(3.16)
Пример 1. Пусть случайная величина  подчиняется нормальному закону распределения вероятностей с параметрами
подчиняется нормальному закону распределения вероятностей с параметрами 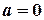 ,
, 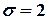 .
.
Определить:
1) 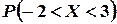 ; 2)
; 2) 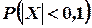 ;
;
Решение: 1) Используя формулу (3.15), имеем
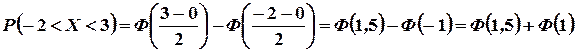
Из таблицы II находим, что 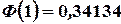 ,
, 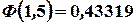 . Следовательно
. Следовательно
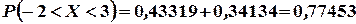
2) Так как 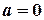 , то
, то 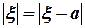 . По формуле (3.16) находим
. По формуле (3.16) находим
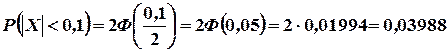
Пример 2. В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы 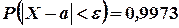 .
.
Решение: По формуле (37) имеем
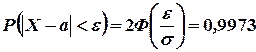 .
.
Следовательно, 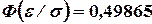 . Из табл. II находим, что этому значению
. Из табл. II находим, что этому значению 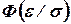 соответствует
соответствует 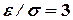 , откуда
, откуда 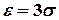 .
.
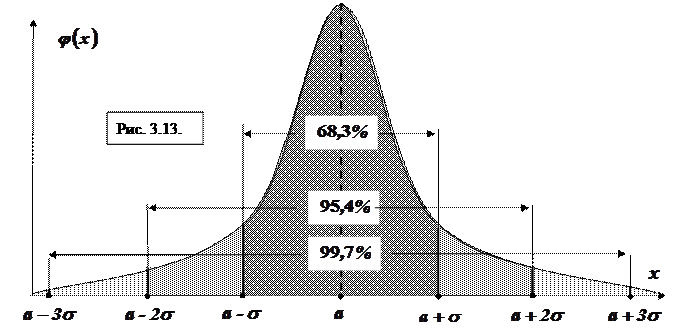
Из последнего примера следует, что если случайная величина подчиняется нормальному закону распределения, то можно утверждать с вероятностью, равной 0,9973, что случайная величина находится в интервале 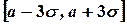 . Так как данная вероятность близка к единице, то можно считать, что значения нормально распределенной случайной величины практически не выходят за границы интервала
. Так как данная вероятность близка к единице, то можно считать, что значения нормально распределенной случайной величины практически не выходят за границы интервала 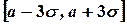 . Этот факт называют правилом трех сигм.
. Этот факт называют правилом трех сигм.
Аналогично можно посчитать, что вероятность того, что случайная величина, распределенная по нормальному закону, заключена в интервале 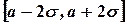 , равна 95,44 % .Соответственно в интервале
, равна 95,44 % .Соответственно в интервале 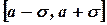 равна 67,26 % .То есть:
равна 67,26 % .То есть:
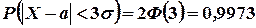
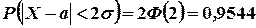
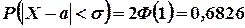
Данные условия наглядно изображены на рис. 3.13.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Оглавление.
1. Дискретные случайные величины.
2. Часто встречающиеся распределения дискретной случайной величины.
3. Функция распределения вероятностей случайной величины и ее свойства.
4. Непрерывные случайные величины.
5. Равномерное распределение.
6. Нормальное распределение.
7. Экспоненциальное распределение.
8. Двумерные случайные величины.
Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, является число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д.
Таким образом, случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное числовое значение.
В дальнейшем мы рассмотрим два типа случайных величин — дискретные и непрерывные.
1. Дискретные случайные величины.
Рассмотрим случайную величину (случайные величины будем обозначать прописными буквами латинского алфавита: 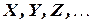 )
)  , возможные значения которой образуют конечную или бесконечную последовательность чисел
, возможные значения которой образуют конечную или бесконечную последовательность чисел 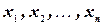 . Такая случайная величина
. Такая случайная величина  называется дискретной (прерывной).
называется дискретной (прерывной).
На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные. Поэтому
для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.
Важнейшей характеристикой случайной величины служит ее распределение вероятностей.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) или графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности:
 | 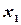 | 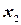 | … | 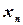 |
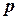 | 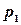 | 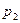 | … | 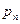 |
Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события 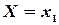 ,
, 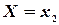 , …,
, …, 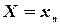 образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:
образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:
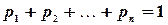 .
.
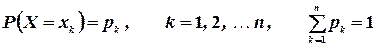 (3.1)
(3.1)
Эту таблицу называют рядом распределения случайной величины  . Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости. По горизонтальной оси будем откладывать возможные значения случайной величины
. Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости. По горизонтальной оси будем откладывать возможные значения случайной величины  , а по вертикальной оси - значения функции
, а по вертикальной оси - значения функции 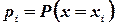 . График функции р(х) изображен на рис. 3.1. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.
. График функции р(х) изображен на рис. 3.1. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.
Пример 3.1. Пусть событие А — появление одного какого-либо очка при бросании игральной кости. Как мы знаем, вероятность выпадения какого-либо очка для всех цифр (1, 2, 3, 4, 5, 6) одинакова и равна Р(A)=1/6. Рассмотрим случайную величину  — число наступлений события А (т.е. число т) при десяти бросаниях игральной кости (т.е. n=10). Значения функции р(х) (закона распределения) приведены в следующей таблице:
— число наступлений события А (т.е. число т) при десяти бросаниях игральной кости (т.е. n=10). Значения функции р(х) (закона распределения) приведены в следующей таблице:
Значения  | … | ||||||||
Вероятности 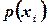 | 0,162 | 0,323 | 0,291 | 0,155 | 0,054 | 0,013 | 0,002 | … |
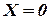 означает, что цифра 1 (или любая другая из шести, могущих выпасть) при десяти бросаний кости не выпала ни разу.
означает, что цифра 1 (или любая другая из шести, могущих выпасть) при десяти бросаний кости не выпала ни разу. 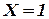 - цифра 1 при десяти бросаний выпала один раз.
- цифра 1 при десяти бросаний выпала один раз. 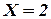 - два раза и т.д.
- два раза и т.д.
Вероятности 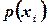 приведенные в таблице, вычислены по формуле Бернулли (
приведенные в таблице, вычислены по формуле Бернулли ( 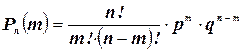 ) при n=10. Для x>6 они практически равны нулю:
) при n=10. Для x>6 они практически равны нулю:
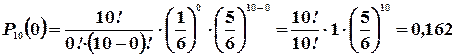
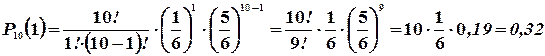
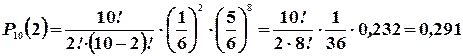
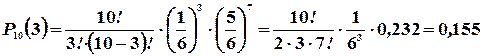
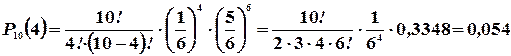
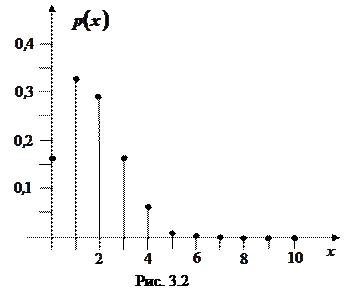
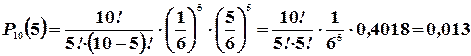
График функции p(x) изображен на рис. 3.2.
Это так называемый биноминальный закон распределения
