Макроэконометрические модели
Макроэконометрическими называют модели, которые описывают корреляционно-регрессионные связи и зависимости, а также закономерности и динамические тенденции, изменения макроуровневых, итоговых народнохозяйственных показателей от затратно-ресурсных. Так, если с их помощью описываются связи и зависимости, то эконометрическими являются модели, на вход которых поступают ресурсы (R1, R2,….,Rn), а на выходе получают величины итоговых (результативных) показателей.
Эконометрическая модель, в которой в качестве результативного показателя принят выпуск продукции, называют производственной функцией.
В качестве ресурсов (факторов производства) на макроуровне наиболее часто рассматриваются накопленный труд в форме производственных фондов (капитал) К и живой труд L, а в качестве результата – валовой выпуск Х (либо валовой внутренний доход N).
Пусть экономика описывается эконометрической моделью в форме нелинейной производственной функции (ПФ):
Х=F(K,L), (6.1)
т.е. выпуск (продукции) есть функция от затрат ресурсов (фондов и труда).
ПФ Х=F(K,L) называется неоклассической, если она является гладкой и удовлетворяет следующим условиям:
1) 
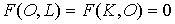
при отсутствии одного из ресурсов производство невозможно;
2) 
, 
c ростом ресурсов выпуск растет;
3) 
, 
c увеличением ресурсов скорость роста выпуска замедляется;
4) 
при неограниченном увеличении одного из ресурсов выпуск неограниченно растет.
Рассмотрим мультипликативную производственную функцию
, 
, 
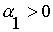, (6.2)
где А – коэффициент нейтрального технического прогресса;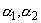 
- коэффициенты эластичности по труду и фондам.
Частным случаем этой функции является известная функция Кобба- Дугласа:
, 
. (6.3)
Логарифмируя эту функцию, получаем
,
т.е. в логарифмах функции (6.3) и (6.2) линейны и являются моделями множественной регрессии, где параметры А, 
, 
могут быть определены по методу наименьших квадратов.
Можно показать (доказать), что производственная функция (6.2) является неоклассической, т.е. отвечает вышеперечисленным условиям 1-4.
Производственная функция называется однородной степени 
, если,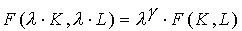 
.
Очевидно, функция (6.2) является однородной степени 
.
Для однородных производственных функций можно ввести понятие эластичности замены одного ресурса другим (труда фондами и наоборот), которая рассчитывается по формулам:
(6.4)
где 
- фондовооруженность, 
– предельная норма замены труда фондами.
Эта величина показывает, на сколько процентов надо изменить фондовооруженность, чтобы добиться изменения нормы замены на 1%. Аналогично вводится и показатель эластичности замены фондов трудом 
.
Можно показать что, 
Для функции (6.2) 
Класс производственных функций с постоянной эластичностью замены, 
называется СES – функциями:
, (6.5)
где 
.
При 
СES – функция стремится к функции Кобба-Дугласа.
При 
СES – функция переходит в линейную ПФ: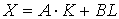 
.
Разработкой макроэконометрических моделей занимался Л.Клейн. По Клейну, такие макроэкономические показатели, как валовой национальный продукт, расходы федерального правительства, ставка процента и цены, являются «движущей силой» региональных моделей.
В 1950 г. Л. Клейн предложил динамическую модель макроэкономики, (получившую название модель Клейна1.) систему уравнений:
- потребление,
- инвестиции,
- зарплата в частном секторе,
- совокупный спрос в равновесии,
- доход частного сектора,
- капитал.
Переменные, стоящие в левых частях уравнений, являются эндогенными. Экзогенными переменными в данной модели являются: G-государственные расходы, не включающие зарплату, Т- непрямые налоги плюс чистый доход от экспорта, 
- зарплата в государственном секторе, 
- временный тренд (в годах, начиная с 1931г.). Кроме того, включены три предопределенные (лагированные) переменные. Таким образом, модель содержит три поведенческих уравнения, одно уравнение равновесия и два тождества.