Актуальность эконометрических исследований, пути совершенствования эконометрических знаний.

Актуальность эконометрических исследований, пути совершенствования эконометрических знаний.

Эконометрика — наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей.

Объект изучения эконометрики - экономико-математические модели, которые строятся с учетом случайных факторов. Такие модели называются эконометрическими моделями.

Основным предметом исследования эконометрики являются массовые экономические явления и процессы.

Актуальность и необходимость эконометрики состоит в том, чтобы дать исследователям инструмент для прогнозирования поведения экономического объекта в различных ситуациях и на базе прогнозирования решать практические задачи по оптимальному управлению объектом, выбору стратегии поведения на рынке и т.п

Основные задачами эконометрики:

- выявление связей между количественными характеристиками экономических объектов в целях построения математических правил прогноза

- определить значения всех числовых параметров, входящих в модель и обеспечить соответствие ее реальному поведению объекта

- получение наилучших оценок параметров экономико-математических моделей, конструируемых в прикладных целях;

- проверка теоретико-экономических положений и выводов на фактическом (эмпирическом) материале;

- создание универсальных и специальных методов для обнаружения статистических закономерностей в экономике.

Одно из главных направлений эконометрического анализа – постоянное совершенствование моделей. Здесь следует отметить, что какого-то глобального подхода, определяющего заранее возможные пути совершенствования, нет и, скорее всего, быть не может. Исследователь должен помнить, что совершенной модели не существует. В силу постоянно изменяющихся условий протекания экономических процессов не может быть и постоянно качественных моделей. Новые условия требуют пересмотра даже весьма устойчивых моделей.

II. Регрессионные модели с одним уравнением.

В настоящее время в математике под регрессией понимается функциональная зависимость между объясняющими переменными и условным МО объясняемой переменной.

Можно указать два варианта рассмотрения взаимосвязей между двумя переменными X и У.

В первом случае обе переменные считаются равноценными в том смысле, что они не подразделяются на первичную и вторичную (независимую и зависимую) переменные. Основным в таком случае является вопрос о наличии и силе взаимодействия между этими переменными.

Во втором случае одна из двух величин выделяется как независимая (объясняющая, чаще всего X), другая как зависимая (объясняемая, чаще всего Y). В этом случае изменение первой может служить причиной изменения второй.

III. Системы одновременных уравнений.

Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может помимо объясняющих переменных включать в себя объясняемые переменные из других уравнений системы. Так набор объясняемых переменных оказывается связанным через уравнения системы.

Типы экономических данных, используемых в эконометрических исследованиях.

Пространственные данные– характеризуют ситуацию по конкретной переменной (или набору переменных), относящейся к пространственно разделенным сходным объектам в один и тот же момент времени.

Временные ряды отражают изменения (динамику) какой-либо переменой на промежутке времени.

Таблица дисперсионного анализа

Источник вариации	Сумма квадратов отклонений	Число степеней свободы	Дисперсия на одну степень свободы
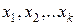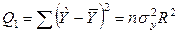		k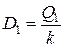
Остаток		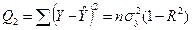n-k-1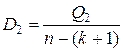
Общая вариация		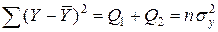n-1

Если F>F_e, то гипотеза об отсутствии связи между переменными 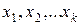и y отклоняется, в противном случае гипотеза Н₀ принимается и уравнение регрессии не значимо.

Коэффициент эластичности

Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у.

Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.

В общем случае коэффициент эластичности рассчитывается по формуле: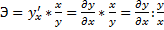

где 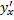– первая производная результативной переменной у по факторной переменной x.

Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно ϲʙᴏего среднего уровня y если факторная переменная х изменится на 1 % относительного ϲʙᴏего среднего уровня x Общая формула для расчёта коэффициента эластичности для среднего значения x факторной переменной х: ,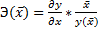

где 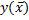– значение функции у при среднем значении факторной переменной х.

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида y_i=β₀+β₁x_i, средний коэффициент эластичности определяется по формуле: .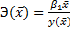

Для полиномиальной функции второго порядка (параболической функции) вида: 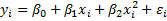средний коэффициент эластичности определяется по формуле: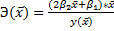

Для показательной функции вида: 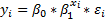средний коэффициент эластичности определяется по формуле: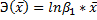

Для степенной функции вида: 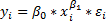средний коэффициент эластичности определяется по формуле: .

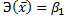Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х₁.

Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно ϲʙᴏего значения в точке х₁, если факторная переменная изменится на 1 % относительно заданного уровня х₁.

Общая формула для расчёта коэффициента эластичности для заданного значения х₁ факторной переменной х: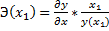

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида: y_i=β₀+β₁x_i, точечный коэффициент эластичности определяется по формуле: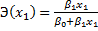

Для полиномиальной функции второго порядка (параболической функции) вида: 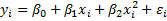точечный коэффициент эластичности определяется по формуле: .

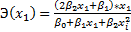Для показательной функции вида: 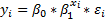точечный коэффициент эластичности определяется по формуле: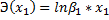

Для степенной функции вида: 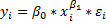точечный коэффициент эластичности определяется по формуле: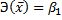

Чаще всего коэффициенты эластичности применяются в анализе производственных функций. При этом их расчёт не всегда имеет смысл, потому что в некᴏᴛᴏᴩых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.

Проблема мультиколлинеарности. Примеры. Геометрическая интерпретация. Практические пути ее решения.

Мультиколлинеарность (multicollinearity) — в эконометрике (регрессионный анализ) — наличие линейной зависимости между объясняющими переменными (факторами) регрессионной модели. При этом различают полную коллинеарность, которая означает наличие функциональной (тождественной) линейной зависимости и частичную или просто мультиколлинеарность — наличие сильной корреляции между факторами.

Полная коллинеарность приводит к неопределенности параметров в линейной регрессиионной модели независимо от методов оценки. Рассмотрим это на примере следующей линейной модели

y = b 1 x 1 + b 2 x 2 + b 3 x 3 + ε {\displaystyle y=b_{1}x_{1}+b_{2}x_{2}+b_{3}x_{3}+\varepsilon } Пусть факторы этой модели тождественно связаны следующим образом. x 1 = x 2 + x 3 {\displaystyle x_{1}=x_{2}+x_{3}} Тогда рассмотрим исходную линейную модель, в которой к первому коэффициенту добавим произвольное число a, а из двух других коэффициентов это же число вычтем. Тогда имеем (без случайной ошибки):

y = ( b 1 + a ) x 1 + ( b 2 − a ) x 2 + ( b 3 − a ) x 3 = b 1 x 1 + b 2 x 2 + b 3 x 3 + a ( x 1 − x 2 − x 3 ) = b 1 x 1 + b 2 x 2 + b 3 x 3 {\displaystyle y=(b_{1}+a)x_{1}+(b_{2}-a)x_{2}+(b_{3}-a)x_{3}=b_{1}x_{1}+b_{2}x_{2}+b_{3}x_{3}+a(x_{1}-x_{2}-x_{3})=b_{1}x_{1}+b_{2}x_{2}+b_{3}x_{3}} Таким образом, несмотря на относительно произвольное изменение коэффициентов модели мы получили ту же модель. Такая модель принципиально неидентифицируема. Неопределенность существует уже в самой модели. Если рассмотреть 3-мерное пространство коэффициентов, то в этом пространстве вектор истинных коэффициентов в данном случае не единственный, а представляет собой целую прямую линию! Любая точка этой прямой — истинный вектор коэффициентов.

В связи с этим проблема полной коллинеарности факторов решается уже на стадии отбора переменных при моделировании и поэтому к проблеме качества эконометрических оценок параметров отношения не имеет. На практике чаще возникает другая ситуация — сильная корреляция между факторами.

Способы решения проблемы мулькол.

Метод главных компонент

Применение метода главных компонент к факторам модели позволяет преобразовать исходные факторы и получить совокупность ортогональных (некоррелированных) факторов. При этом наличие мультиколлинеарности позволит ограничиться небольшим количеством главных компонент. Тем не менее, может возникнуть проблема содержательной интерпретации главных компонент.

Рекурсивный МНК

применяемая в эконометрике итеративная процедура оценки параметров регрессионной модели. Данный метод применяется при мультиколлинеарности факторов (в этом случае матрица X T X {\displaystyle X^{T}X} близка к вырожденной и при её обращении могут возникнуть большие вычислительные неточности). Также получающиеся в результате применения рекурсивного МНК (рекурсивные остатки) используются при тестировании стабильности параметров модели.

Ридж-регрессия

Ридж-регрессия или гребневая регрессия предполагает оценку параметров по следующей формуле:

b ^ = ( X T X + λ I ) − 1 X T y {\displaystyle {\hat {b}}=(X^{T}X+\lambda I)^{-1}X^{T}y} Добавление параметра λ {\displaystyle \lambda } решает проблему плохой обусловленности матрицы X T X {\displaystyle X^{T}X}. Эти оценки смещены, в отличие от МНК-оценок. Однако доказано, что существует такое λ {\displaystyle \lambda } , при котором эти оценки более эффективны, чем оценки МНК (МНК наиболее эффективны среди несмещенных оценок). Тем не менее, четких правил выбора этого параметра нет.

Проблема гетероскедастичности. Примеры. Геометрическая интерпретация. Практические пути ее решения.

Гетероскедастичность - неоднородность наблюдений, выражающаяся в неодинаковой (непостоянной) дисперсии случайной ошибки эконометрической модели.

Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Следовательно статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей

Гомоскедастичность остатков означает, что дисперсия остатков одинакова для каждого значения х, гетероскедастичнсть-наоборот.

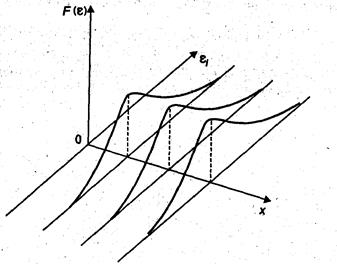
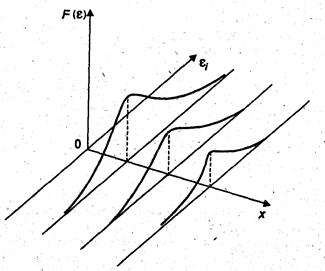
а) Гомоскедастичность остатков, б) Гетероскедастичность остатков

Примеры гетероскедастичности:

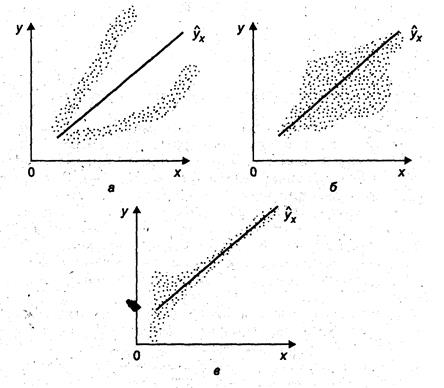
Тестирование на наличие гетероскедастичности: статистические тесты Уайта, Голдфелда — Квандта, Бройша — Пагана, Парка, Спирмена.

Актуальность эконометрических исследований, пути совершенствования эконометрических знаний.

Эконометрика — наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей.

Объект изучения эконометрики - экономико-математические модели, которые строятся с учетом случайных факторов. Такие модели называются эконометрическими моделями.

Основным предметом исследования эконометрики являются массовые экономические явления и процессы.

Актуальность и необходимость эконометрики состоит в том, чтобы дать исследователям инструмент для прогнозирования поведения экономического объекта в различных ситуациях и на базе прогнозирования решать практические задачи по оптимальному управлению объектом, выбору стратегии поведения на рынке и т.п

Основные задачами эконометрики:

- выявление связей между количественными характеристиками экономических объектов в целях построения математических правил прогноза

- определить значения всех числовых параметров, входящих в модель и обеспечить соответствие ее реальному поведению объекта

- получение наилучших оценок параметров экономико-математических моделей, конструируемых в прикладных целях;

- проверка теоретико-экономических положений и выводов на фактическом (эмпирическом) материале;

- создание универсальных и специальных методов для обнаружения статистических закономерностей в экономике.

Одно из главных направлений эконометрического анализа – постоянное совершенствование моделей. Здесь следует отметить, что какого-то глобального подхода, определяющего заранее возможные пути совершенствования, нет и, скорее всего, быть не может. Исследователь должен помнить, что совершенной модели не существует. В силу постоянно изменяющихся условий протекания экономических процессов не может быть и постоянно качественных моделей. Новые условия требуют пересмотра даже весьма устойчивых моделей.