Синтез рекурсивных фильтров по аналоговому прототипу

При синтезе стандартных частотно-избирательных фильтров удобно воспользоваться хорошо разработанным аппаратом расчета аналоговых фильтров. Наиболее широкое распространение получили следующие методы:

1. Метод инвариантности импульсной характеристики (метод стандартного 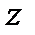- преобразования).

2. Метод билинейного 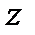- преобразования.

3. Метод замены производных конечными разностями.

4.2.1. Метод инвариантности импульсной характеристики (метод стандартного 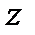- преобразования)

Под инвариантностью импульсной характеристики понимается равенство отсчетов импульсной характеристики цифрового фильтра значениям импульсной характеристики аналогового прототипа, взятым с периодом дискретизации.

Для реализации метода необходимо:

- найти импульсную характеристику прототипа ;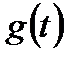

- получить импульсную характеристику цифрового фильтра 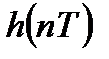путем дискретизации 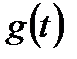с периодом 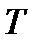с учетом масштабирующего множителя :

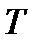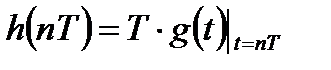; (4.1)

- найти передаточную функцию фильтра, взяв 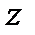- преобразование от :

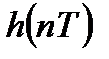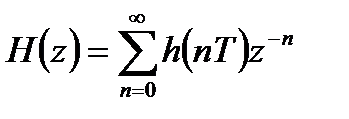. (4.2)

Рисунок 3.1 – дискретизация импульсной характеристики аналогового прототипа

Предположим, что передаточная функция аналогового прототипа записана в виде суммы простейших дробей:

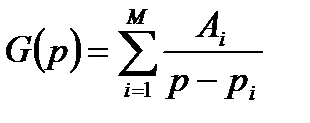. (4.3)

В этом случае в соответствии с обратным преобразованием Лапласа импульсная характеристика аналогового прототипа имеет следующий вид:

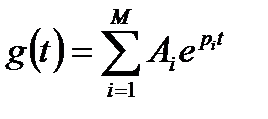. (4.4)

После дискретизации получим требуемую импульсную характеристику ЦФ:

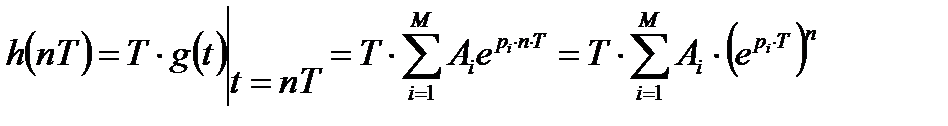. (4.5)

Передаточная функция синтезированного цифрового фильтра в результате применения 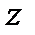- преобразования имеет следующий вид:

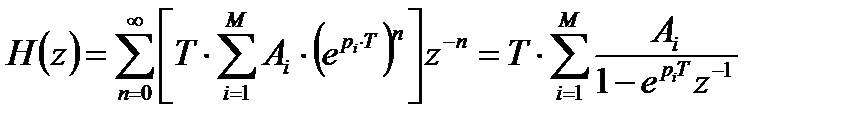. (4.6)

Полученная передаточная функция соответствует параллельной структуре цифрового фильтра. Структурная схема одного звена синтезированного цифрового фильтра с передаточной характеристикой 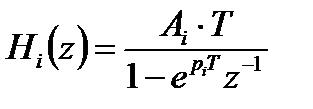имеет следующий вид: рисунок 3.2.

Рисунок 3.2 – структурная схема одного звена цифрового фильтра

Таким образом, процедура синтеза ЦФ методом инвариантности импульсной характеристики содержит следующие шаги:

1. Задать требования к цифровому фильтру.

2. Рассчитать нули и полюса аналогового фильтра-прототипа и построить его передаточную функцию .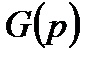

3. Разложить 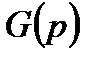на простейшие дроби.

4. Записать передаточную функцию цифрового фильтра 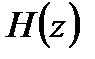на основе соотношений (4.3) и (4.6).

Частотная характеристика полученного фильтра связана с частотной характеристикой аналогового прототипа таким же образом, как спектр дискретизированного сигнала связан со спектром аналогового сигнала: периодическим повторением. Поэтому для получения хороших результатов для данного метода коэффициент передачи аналогового прототипа должен быть пренебрежимо малым на частотах, превышающих частоту Найквиста. Следовательно, метод подходит для создания ФНЧ и ПФ, но неприменим для разработки ФВЧ и РФ.

Пример использования метода инвариантности импульсной характеристики

Пусть передаточная функция аналогового прототипа имеет следующий вид:

.

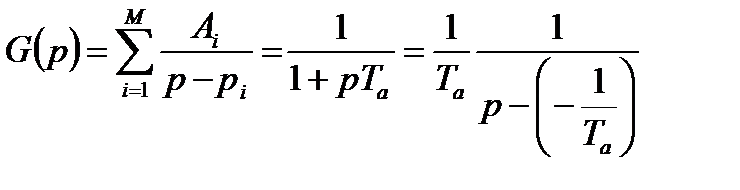Таким образом, в соответствии с выражением (4.3) можно записать следующие параметры аналогового прототипа:

,

.

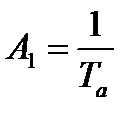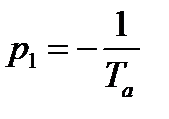В соответствии с выражением (4.6) получим следующее выражение для передаточной функции искомого цифрового фильтра:

.

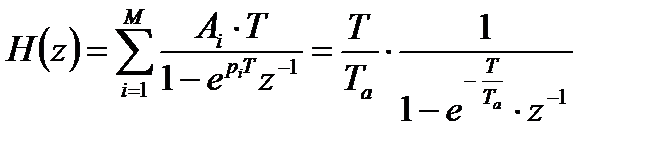Получим уравнение цифровой фильтрации. Для этого запишем передаточную функцию цифрового фильтра в виде:

,

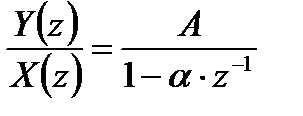где ,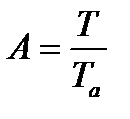

.

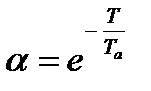В результате ряда математических преобразований последнего выражения можно получить:

,

,

.

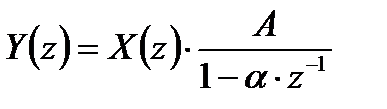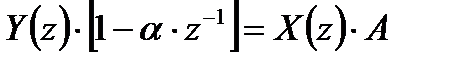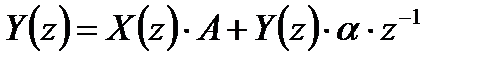После перехода от изображений z-преобразования к оригиналам, получим уравнение цифровой фильтрации:

.

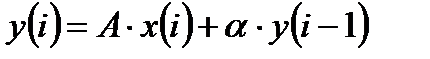4.2.2. Метод билинейного 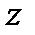- преобразования

Преобразование Лапласа и 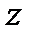- преобразование связаны между собой соотношением:

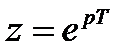. (4.7)

Выражение (4.7) непосредственно не может быть использовано для расчета цифрового фильтра при известной передаточной характеристике аналогового прототипа, так как обратное соотношение является транцендентным:

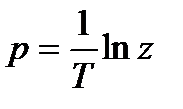. (4.8)

Это затруднение преодолевается использованием разложения в ряд:

.

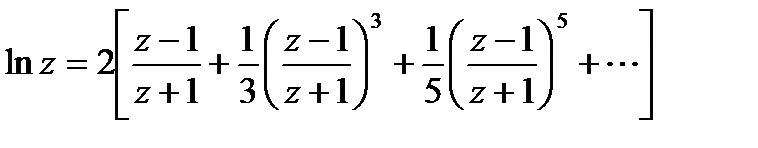Используя первый член разложения, можно получить:

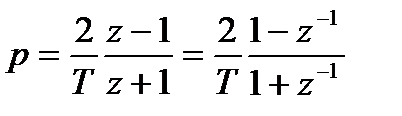. (4.9)

Данное преобразование представляет собой дробно-рациональную функцию первого порядка от аргумента 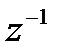и называется билинейным z – преобразованием.

Передаточная функция цифрового фильтра 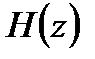получается из передаточной функции аналогового прототипа 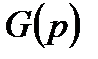применением следующей замены:

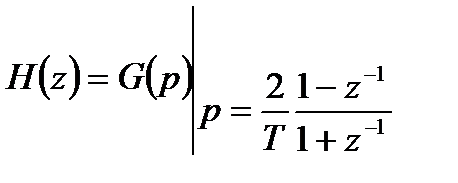. (4.10)

Рассмотрим свойства билинейного преобразования. Для этого получим:

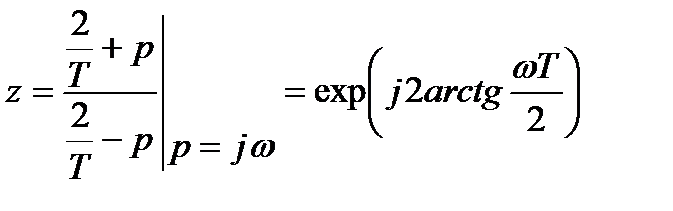. (4.11)

Таким образом, билинейное преобразование приводит к существенной деформации АЧХ аналога-прототипа при его пересчете в цифровую форму по сравнению с исходным соотношением 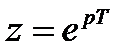. Связь между частотами АЧХ прототипа 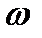и частотами цифрового фильтра определяются из соотношения:

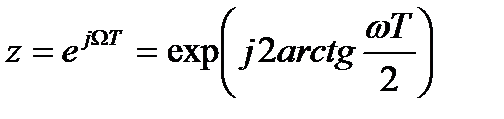
или

.

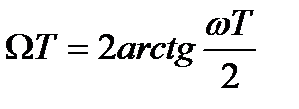Окончательно связь между частотой аналогового прототипа и частотой цифрового фильтра имеет следующий вид:

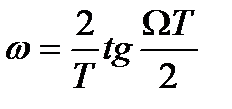. (4.12)

В соответствии с последним выражением вся ось бесконечная ось АЧХ аналогового прототипа полностью помещается в интервале Найквиста на оси цифровых частот от 0 до 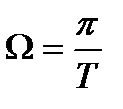: рисунок 3.3. Следовательно, полностью исключается эффект наложения копий частотных характеристик, свойственный методу инвариантности импульсной характеристики. В области малых частот частотные характеристики аналогового и цифрового фильтров совпадают:

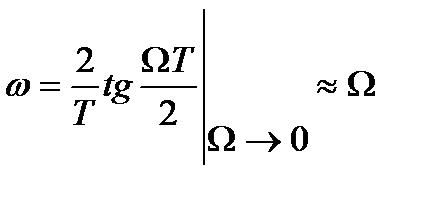. (4.13)

Рисунок 3.3 – трансформация частотной оси при билинейном преобразовании

Эффект деформации АЧХ легко учитывается для частотно-избирательных фильтров, характеризуемых границами полосы пропускания, с использованием последнего выражения связи частот.

Порядок расчета фильтра следующий:

1) АЧХ рассчитываемого фильтра задается в масштабе частот и в этом же масштабе отмечаются характерные точки АЧХ.

2) С помощью преобразующей функции 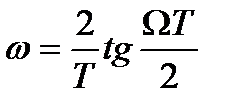определяются те же характерные точки в масштабе частот 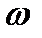для аналогового прототипа и составляется выражение для его передаточной функции .

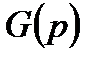3) Методом билинейного преобразования передаточная функция 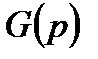пересчитывается в передаточную функцию 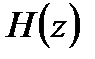цифрового фильтра.

Таким образом, устранен недостаток, связанный с деформацией ФЧХ аналогового прототипа.

Метод билинейного преобразования полностью исключает эффект наложения АЧХ, не требует повышения частоты дискретизации для уменьшения ошибок воспроизведения АЧХ. Метод используется, когда не требуется повышенная точность воспроизведения АЧХ аналогового прототипа.

Пример использования метода билинейного преобразования

Пусть передаточная функция аналогового прототипа описывается выражением:

.

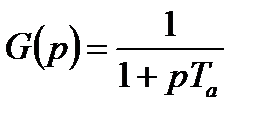С учетом выражения (4.10) можно получить следующее выражение для передаточной функции искомого цифрового фильтра:

,

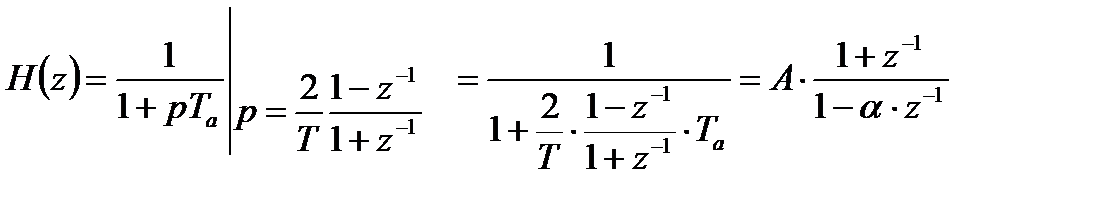где ;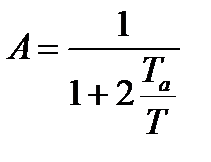

.

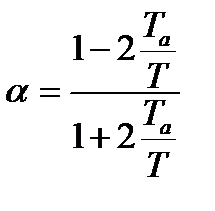Для получения уравнения цифровой фильтрации запишем передаточную функцию в следующем виде:

.

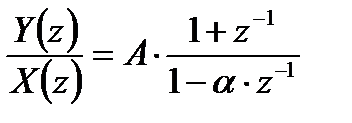После ряда математических преобразований последнего выражения можно получить:

,

,

.

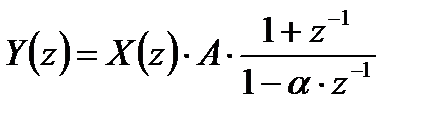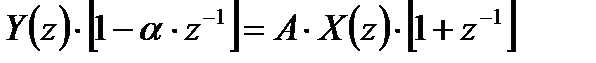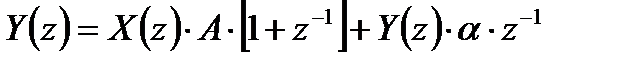После перехода от изображений z-преобразования к оригиналам, получим уравнение цифровой фильтрации:

.

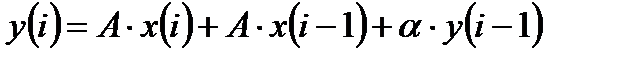4.2.3. Метод замены производных конечными разностями

Метод основан на замене производных конечными разностями:

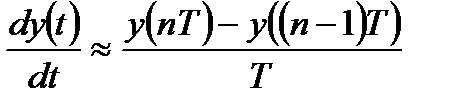; (4.14)

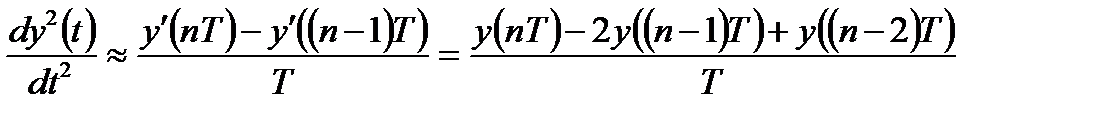. (4.15)

Установим связь аргументов преобразования Лапласа 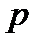и z-преобразования 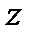с использованием выражения (4.14). В этом случае можно записать:

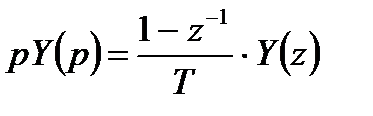. (4.16)

Соответственно можно получить следующую связь аргументов:

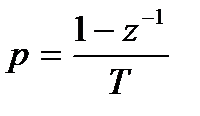. (4.17)

Передаточная функция цифрового фильтра 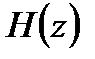получается из передаточной функции аналогового прототипа 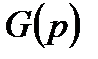применением следующей замены:

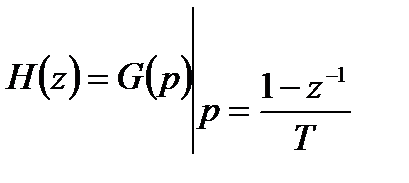. (4.18)

Пример использования метода замены производных конечными разностями

Пусть передаточная функция аналогового прототипа описывается выражением:

.

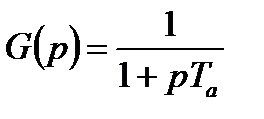С учетом выражения (3.18) можно получить следующее выражение для передаточной функции искомого цифрового фильтра:

,

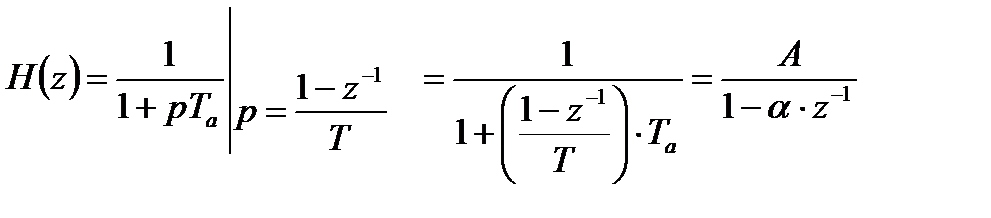где ;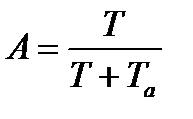

.
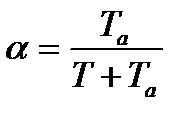