Тема. Построение графиков функций в электронных таблиц MS Excel.

Цель работы. Изучение графических возможностей электронных таблиц MS Excel, приобретение навыков работы с Мастером диаграмм в электронных таблицах.

Задание. Построить графики функций из табл. 5 – 8.

Таблица 5. Варианты заданий

№	f(x)	№	f(x)	№	f(x)

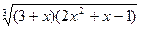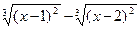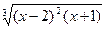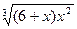Таблица 6. Варианты заданий

№	f(x)	№	f(x)	№	f(x)

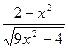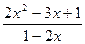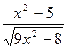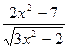Таблица 7. Варианты заданий

№	f(x)	№	f(x)	№	f(x)

Таблица 8. Варианты заданий

№	f(x,y)	№	f(x,y)	№	f(x,y)
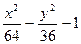	y2 - 2x2 - 4		y2 +4x2 - 4		2y2 - 9x2 –18
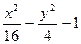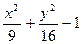	9y2 - 4x2 – 16		9y2 + 4x2 – 16		2y2 +9x2 – 81

Рекомендации к выполнению лабораторной работы. Рассмотрим несколько примеров.

Пример 1. Построить график функции (рис. 14).

Определим функцию f(x). Для этого в ячейки А1:А21 необходимо ввести значение аргумента при помощи автозаполнения, в данном случае с шагом 0,5[35]. В ячейку В1 вводится значение функции: В1=(A1^2*(A1+3))^(1/3). Ячейки В2:В21 заполняются копированием формулы из ячейки В1.

Рис. 14. График функции

Далее выделим диапазон А1:В21 и воспользуемся Мастером диаграмм. Для построения графика функции лучше выбрать точечную диаграмму, со значениями, соединенными сглаживающими линиями без маркеров. Чтобы график получился выразительным, можно определить промежуток изменения аргумента, увеличить толщину линий, выделить оси координат, нанести на них соответствующие деления, сделать подписи на осях и вывести заголовок.

Пример 2. Построить график функции f(x)= (рис. 15).

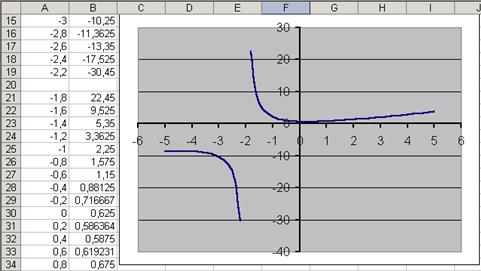
Рис. 15. График функции f(x)=

При построении этого графика следует обратить внимание на область определения функции. В данном случае функция не существует при обращении знаменателя в ноль. Решим уравнение:

.

Следовательно, при 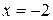функция не определена. Об этом надо помнить при определении значений аргумента. На рис. 15 видно, что значение аргумента задано с шагом 0.2, в два этапа, не включая (-2).

Пример 3. Построить график функции .

При построении этого графика следует использовать функцию ЕСЛИ. Например, в ячейке А1 находится начальное значение аргумента, тогда значение функции можно представить формулой:

В1=ЕСЛИ(A1<=0;(1+sin(A1)/(1+2*cos(A1));(1+A1)^0.5).

Пример 4. Изобразить линию заданную неявно уравнением: 4y² +5x² – 20=0.

Данная функция f(x,y)=0описывает кривую линию под названием эллипс. В связи с тем, что линия задана неявно, для ее построения необходимо разрешить заданное уравнение относительно переменной y:

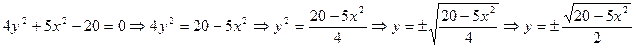
Понятно, что линию f(x,y) можно изобразить, построив графики двух функций в одной графической области. Причем определены эти функции только в диапазоне от -2 до 2[36].

Рис. 16. Эллипс

Итак, введем значения аргумента (от -2 до 2 с шагом 0,1), например, в диапазон А3:А43 (рис. 1.29).Определим функции формулами:

В3= КОРЕНЬ(20-5*$A3^2)/2 и С3=-КОРЕНЬ(20-5*$A3^2)/2.

Далее скопируем эти формулы до В43 и С43соответственно.

Затем выделим диапазон А3:С43 и воспользовавшись Мастером диаграмм, построим графики функций 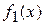и в одной графической области (рис. 16).

ЛАБОРАТОРНАЯ РАБОТА №5