Частотные характеристики звеньев
Если подать на вход динамического звена сигнал вида 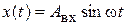 или в форме Эйлера
или в форме Эйлера 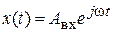 , то выходной сигнал будет иметь вид
, то выходной сигнал будет иметь вид 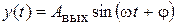 или в форме Эйлера
или в форме Эйлера 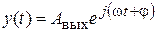 . Отношение выходного сигнала к входному называется частотной передаточной функцией:
. Отношение выходного сигнала к входному называется частотной передаточной функцией:
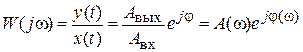 .
.
Здесь A(ω) – модуль частотной передаточной функции (отношение амплитуд выходного и входного сигналов), φ(ω) – аргумент частотной передаточной функции (сдвиг фазы выходного сигнала относительно входного).
Частотная передаточная функция является комплексной, и в ней можно выделить действительную и мнимую части:
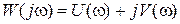 .
.
Пользуясь такой моделью, можно получить ряд частотных характеристик звена.
1. Амплитудно-фазочастотная характеристика (АФЧХ) – изображение частотной передаточной функции на комплексной плоскости (U, V) при изменении частоты от 0 до ∞.
2. Амплитудно-частотная характеристика (АЧХ) – зависимость модуля частотной передаточной функции от частоты:
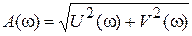 .
.
3. Фазочастотная характеристика (ФЧХ) – зависимость аргумента частотной передаточной функции от частоты:
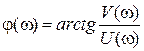 .
.
4. Вещественная частотная характеристика (ВЧХ) – зависимость вещественной части передаточной функции от частоты P = U(ω).
5. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) – форма представления АЧХ, когда по оси абсцисс откладывается частота в логарифмическом масштабе, по оси ординат – модуль частотной передаточной функции в децибелах:
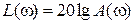 .
.
6. Логарифмическая фазочастотная характеристика (ЛФЧХ) – отличается от ФЧХ логарифмическим масштабом оси абсцисс (частот), масштаб оси ординат обычный.
Временные и частотные характеристики типовых звеньев приведены ниже.
Позиционные звенья
В зависимости от вида полинома C(p) имеют следующие разновидности.
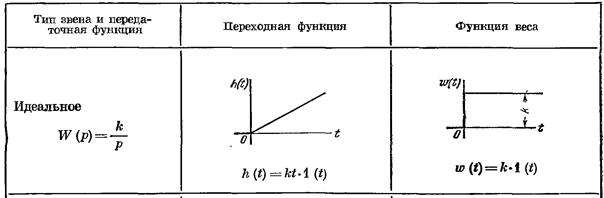
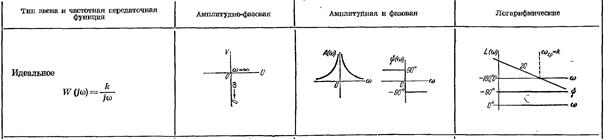
1. Безынерционное (идеальное, усилительное) звено.
Уравнение звена 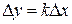 , передаточная функция W(p) = k.
, передаточная функция W(p) = k.
Как видно из уравнения, звено изменяет только уровень входного сигнала, не меняя его форму. Безынерционными считают звенья, инерционностью которых можно пренебречь: делители напряжения, рычаги и т. д.


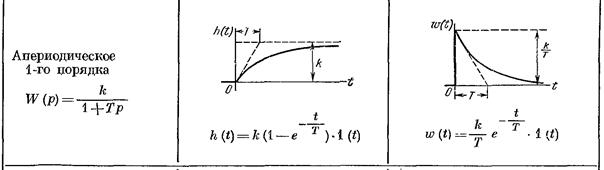
2. Апериодическое звено 1-го порядка.
Уравнение звена 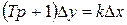 , передаточная функция
, передаточная функция 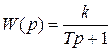 .
.
В процессе работы звена проявляется его инерционность, которая оценивается постоянной времени T. Для апериодических звеньев 1-го порядка T соответствует времени, за которое выходная величина достигает 63% установившегося значения.
Примерами звеньев могут служить нагревательные элементы, приводы различных типов (электрические, гидравлические, пневматические), датчики различных величин (терморезисторы, термопары и т. д.).
Пример.Металлические термометры сопротивления имеют практически линейную характеристику, поэтому коэффициент передачи постоянен во всем диапазоне измерений. Например, для платинового термометра сопротивления со стандартной градуировкой Pt100 при повышении температуры от 0 до 20°С сопротивление изменяется от 100,00 до 107,79 Ом. Коэффициент передачи:
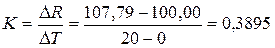 Ом/°С.
Ом/°С.
Для оценки динамических свойств термометров сопротивления нормируется показатель тепловой инерции – время, необходимое для того, чтобы при внесении термометра в среду с постоянной температурой, разность температуры среды и любой точки термометра составила 0,37 значения температуры среды. Следовательно, для термометра сопротивления показатель тепловой инерции и постоянная времени равнозначны.
Например, по паспортным данным термометра сопротивления платинового ТСП-1287 с градуировкой Pt100 показатель тепловой инерции равен 8 с. Следовательно, постоянная времени имеет то же значение, коэффициент передачи рассчитан ранее, и передаточная функция имеет вид
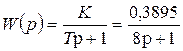 .
.



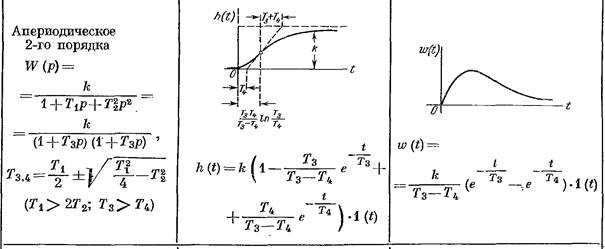
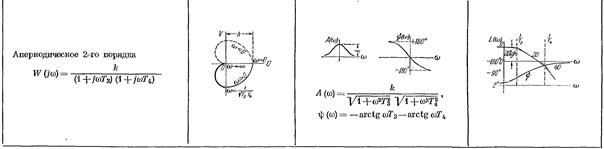
3. Апериодическое звено 2-го порядка.
Уравнение звена 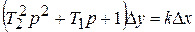 или
или 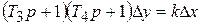 , передаточная функция
, передаточная функция 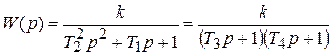 .
.
В данном случае инерционность звена определяется двумя постоянными времени, причем конкретный физический смысл могут иметь как значения T1, T2, T3, T4, так и их комбинации. Например, для двухступенчатого RC-фильтра (рис. 3.3) передаточная функция:
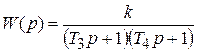 , где T3 = R1C1, T4 = R2C2, k = 1.
, где T3 = R1C1, T4 = R2C2, k = 1.

Рис. 3.3
В этом случае рассматривается последовательное соединение двух апериодических звеньев 1-го порядка.
Для электродвигателя постоянного тока с независимым возбуждением при управлении частотой вращения с помощью напряжения на якоре передаточная функция
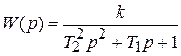 , где
, где 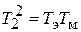 ,
, 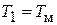 .
.
Здесь Тэ – электрическая постоянная времени; Тм – электромеханическая постоянная времени (подробности их расчета можно узнать из [6]).


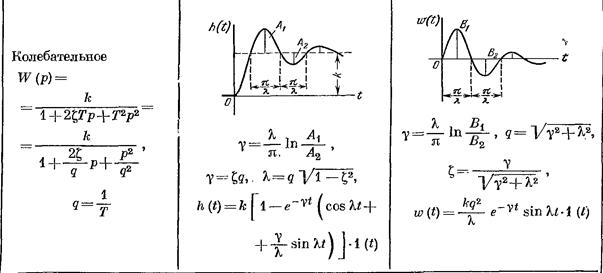
4. Колебательное звено.
Уравнение звена 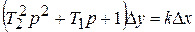 или
или 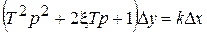 , передаточная функция
, передаточная функция
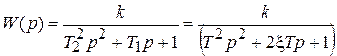 .
.
В отличие от апериодического звена второго порядка здесь T1 < 2T2, и полином не раскладывается на множители вида Tp + 1. Переход звена из одного статического состояния в другое сопровождается затухающими колебаниями выходной величины, причем скорость затухания зависит от параметра затухания ξ, который находится в пределах 0 < ξ < 1. Чем ближе значение параметра к единице, тем быстрее затухают колебания. Частотная характеристика колебательного звена характеризуется наличием резонанса на частоте 1/T.
Примерами колебательных звеньев являются маятник, акселерометр, колебательный контур (рис. 3.4).
Для колебательного контура
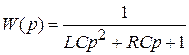 ,
, 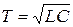 ,
, 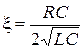 .
.
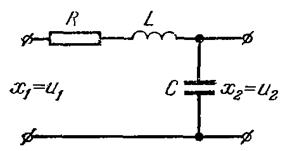
Рис. 3.4 – Последовательный колебательный контур

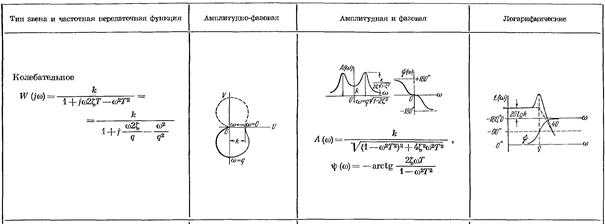
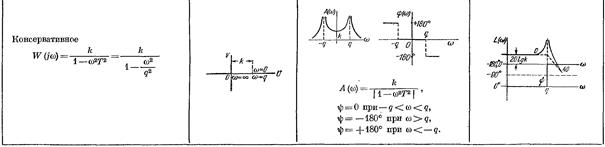
5. Консервативное звено.
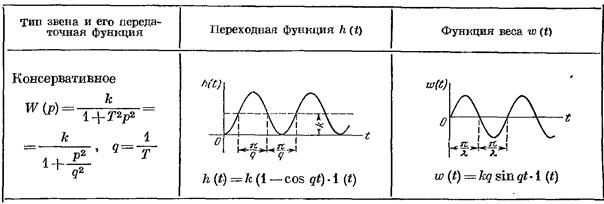
Если в колебательном звене устранить потери энергии или восполнять их из отдельного источника, получим незатухающие колебания. В этом случае ξ = 0, уравнение и передаточная функция имеют вид
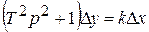 ;
; 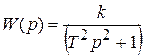
Примерами консервативных звеньев могут служить механические и электрические генераторы.

Интегрирующие звенья
1. Идеальное интегрирующее звено
Уравнение звена 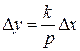 , передаточная функция
, передаточная функция 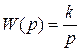 .
.
Как видно из передаточной функции, инерционностью звена при расчетах пренебрегают. К идеальным интегрирующим звеньям можно отнести резервуар с жидкостью (входная величина – расход поступающей жидкости, выходная – уровень жидкости), интегрирующий усилитель (рис. 3.5, а), гидравлический или механический демпфер (цилиндр с поршнем, входная величина – сила на поршне, выходная – его перемещение) (рис. 3.5, б).
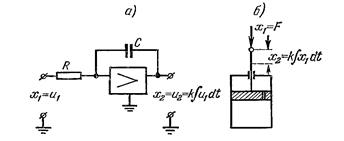
Рис. 3.5
2. Реальное интегрирующее звено (с замедлением)
Если более точно рассматривать уравнения идеальных интегрирующих звеньев и учитывать их инерцию, получим реальные интегрирующие звенья с уравнением 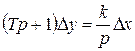 и передаточной функцией
и передаточной функцией 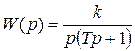 .
.
Примером может служить электродвигатель, если в качестве выходной величины рассматривать не скорость вращения, а угол поворота. Передаточная функция
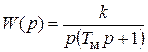 или
или 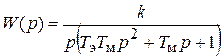 .
.



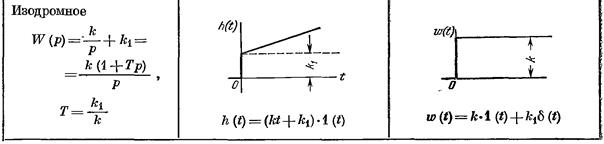
3. Изодромное звено
Представляет собой комбинацию в виде параллельного соединения идеального интегрирующего и безынерционного звеньев и имеет уравнение 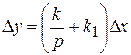 и передаточную функцию
и передаточную функцию 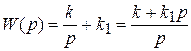 .
.
Примерами могут служить изодромный усилитель (рис. 3.6, а) и пружинно-гидравлический демпфер (рис. 3.6, б).
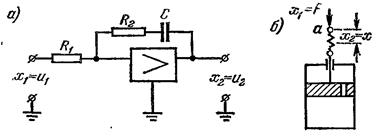
Рис. 3.6
Также можно изодромное звено может быть построено как последовательное соединение идеального интегрирующего и форсирующего звеньев (см. пункт «Дифференцирующие звенья»):
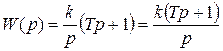 .
.
Таким способом из интегрирующего привода получают форсирующий, что позволяет обеспечить толчок при трогании с места. Это хорошо видно на переходной характеристике и позволяет легче перемещать крупные тяжелые объекты.

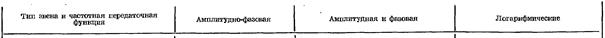

Дифференцирующие звенья
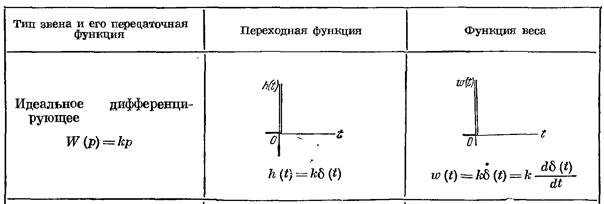
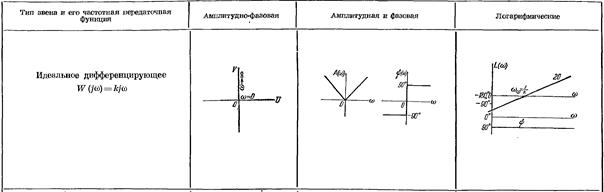
1. Идеальное дифференцирующее звено
Уравнение звена 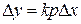 , передаточная функция
, передаточная функция 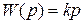 . Как видно из передаточной функции, инерционностью звена при расчетах пренебрегают. К идеальным дифференцирующим звеньям относят тахогенераторы, если входная величина – угол поворота, выходная – напряжение (рис. 3.7, а), дифференцирующий усилитель (рис. 3.7, б).
. Как видно из передаточной функции, инерционностью звена при расчетах пренебрегают. К идеальным дифференцирующим звеньям относят тахогенераторы, если входная величина – угол поворота, выходная – напряжение (рис. 3.7, а), дифференцирующий усилитель (рис. 3.7, б).
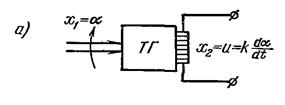
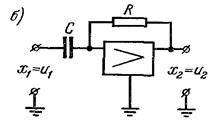
Рис. 3.7
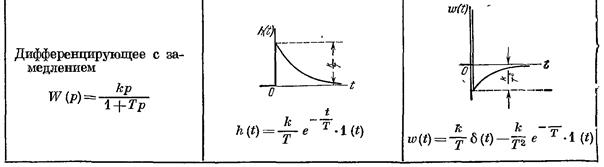
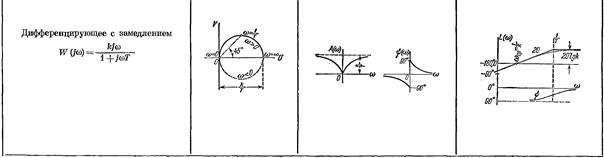
2. Реальное дифференцирующее звено (с замедлением)
Если более точно рассматривать уравнения идеальных дифференцирующих звеньев и учитывать их инерцию, получим реальные дифференцирующие звенья с уравнением 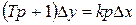 и передаточной функцией
и передаточной функцией 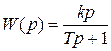 .
.
Дополнительно примерами могут служить RC и RL цепи (рис. 3.8).
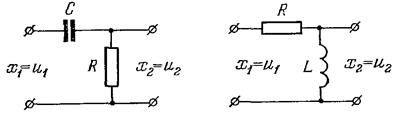
Рис. 3.8


3. Форсирующие звенья
Представляют собой комбинации дифференцирующих и позиционных звеньев:
| Звено | Передаточная функция |
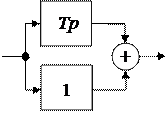 | 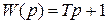 |
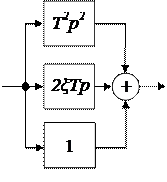 | 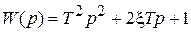 |
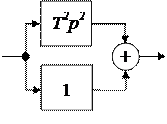 | 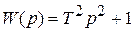 |
Звенья с запаздыванием
Представляют собой комбинацию либого из рассмотренных звеньев и звена чистого запаздывания, которое описывается дифференциально-разностным уравнением 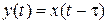 . По теореме запаздывания для преобразования Лапласа передаточная функция
. По теореме запаздывания для преобразования Лапласа передаточная функция 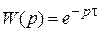 . Переходная характеристика звена представляет собой функцию Хевисайда, смещенную относительно входного сигнала на время запаздывания τ.
. Переходная характеристика звена представляет собой функцию Хевисайда, смещенную относительно входного сигнала на время запаздывания τ.
Примерами звеньев с запаздыванием могут служить акустические линии связи (τ – время прохождения звука), транспортеры (τ – время движения ленты), трубопроводы (τ – время распространения давления).
Для построения АФЧХ любого звена с запаздыванием нужно взять АФЧХ аналогичного звена без запаздывания и каждую ее точку сместить вдоль окружности по часовой стрелке на угол τω, где ω – частота, соответствующая этой точке. На рис. 3.9 показана АФЧХ комбинации апериодического звена 1-го порядка и звена чистого запаздывания, т. е. 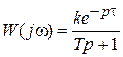 ,
, 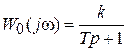 .
.
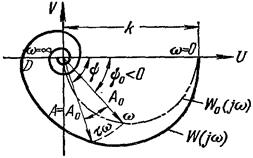
Рис. 3.9
Практическое задание
Часть 1. Исследование временных характеристик звеньев
1. Запустить на выполнение файл «Позиционные звенья.vsm».
2. Для апериодических звеньев 1-го порядка задать значения постоянных времени и коэффициентов передачи. Проанализировать, как влияют заданные параметры на форму временных характеристик.
3. Для апериодических звеньев 2-го порядка задать значения постоянных времени и коэффициентов передачи. Проанализировать, как влияют заданные параметры на форму временных характеристик.
4. Для колебательных звеньев задать значения постоянных времени, коэффициентов передачи и параметров затухания. Проанализировать, как влияют заданные параметры на форму временных характеристик.
5. Для консервативных звеньев задать значения постоянных времени и коэффициентов передачи. Проанализировать, как влияют заданные параметры на форму временных характеристик.
6. Выполнить аналогичные действия с файлами «Интегрирующие звенья.vsm», «Дифференцирующие звенья.vsm».
7. Запустить на выполнение файл «Неизвестное звено.vsm». Запустить процесс моделирования и по полученным временным характеристикам определить передаточную функцию звена.
Часть 2. Исследование частотных характеристик звеньев
1. Запустить на выполнение файл «Позиционные звенья.vsm».
2. Для апериодических звеньев 1-го порядка задать значения постоянных времени и коэффициентов передачи. Выделить одно из звеньев и с помощью меню Analyze – Frequency Response получить ЛАЧХ (Magnitude) и ЛФЧХ (Phase). С помощью меню Analyze – Nyquist Response получить АФЧХ (Imaginary). Для удобства просмотра увеличить размеры окон и включить сетку (Grid Lines в настройках осциллографа). Получить те же характеристики для звена с другими значениями постоянной времени и коэффициента передачи.
3. Те же действия выполнить для других видов позиционных звеньев.
4. Выполнить аналогичные действия с файлами «Интегрирующие звенья.vsm», «Дифференцирующие звенья.vsm».
5. Запустить на выполнение файл «Неизвестное звено.vsm». Запустить процесс моделирования. Получить ЛАЧХ и ЛФЧХ и по ним определить передаточную функцию звена.
Структурные схемы САУ
Структурная схема системы автоматического управления –графическое изображение структуры системы автоматического управления (части системы автоматического управления). Структурные схемы в автоматике используются для отражения взаимодействия динамических звеньев, т.е. представляют собой математические модели системы автоматического управления.
Основные элементы структурной схемы – динамическое звено, узел, сумматор, сравнивающее устройство (вычитатель). Они показаны на рис. 3.10.
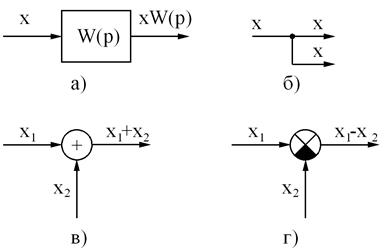
Рис. 3.10. Элементы структурных схем
а – динамическое звено; б – узел; в – сумматор; г – сравнивающее устройство
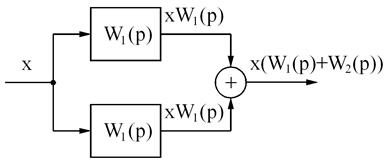
Динамические звенья в структурных схемах могут образовывать различные соединения, основными являются последовательное, параллельное и встречно параллельное (рис. 3.11).
 а) а) | 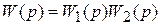 |
 б) б) | 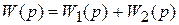 |
 в) в) | 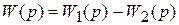 |
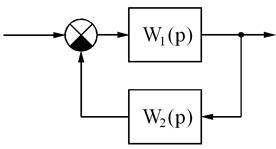 г) г) | 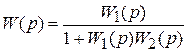 |
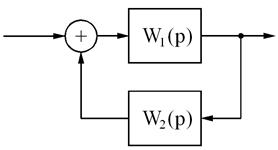 д) д) | 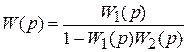 |
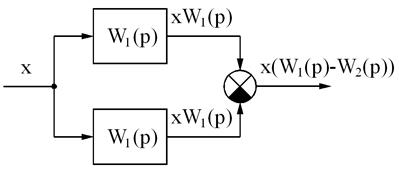
Рис. 3.11. Соединения динамических звеньев
а – последовательное; б – параллельное; в – параллельное с вычитанием;
г – встречно-параллельное с отрицательной обратной связью;
д – встречно-параллельное с положительной обратной связью
Если соединения звеньев имеют сложный вид, общую передаточную функцию получают переходом к основным видам соединений с помощью следующих правил преобразования.
1. Однотипные элементы, расположенные последовательно, можно менять местами:
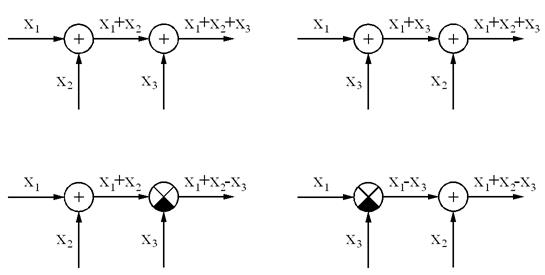
2. Узел можно переносить со входа на выход динамического звена:

3. Узел можно переносить с выхода на вход динамического звена:
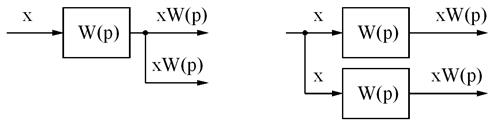
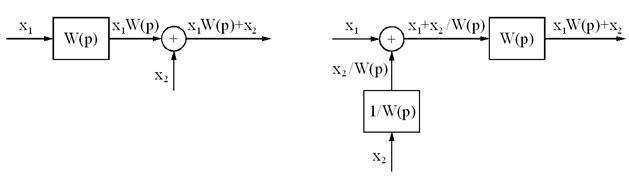
4. Сумматор (сравнивающее устройство) можно переносить со входа на выход динамического звена:
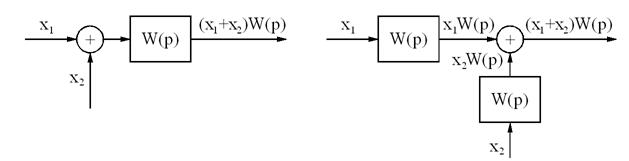
5. Сумматор (сравнивающее устройство) можно переносить с выхода на вход динамического звена:
6. Узел можно переносить с выхода на вход сумматора:
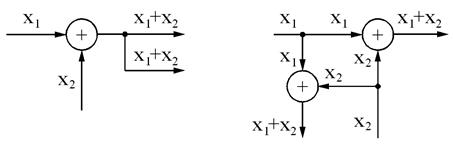
7. Можно переходить к единичной обратной связи:

Пример преобразования схемы.
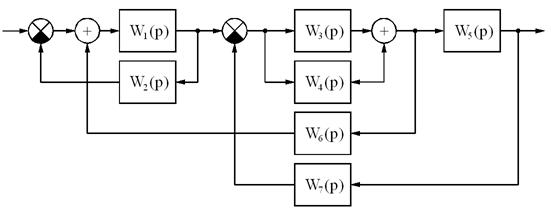
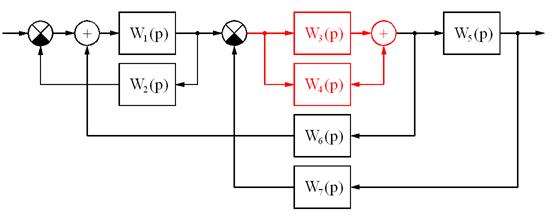
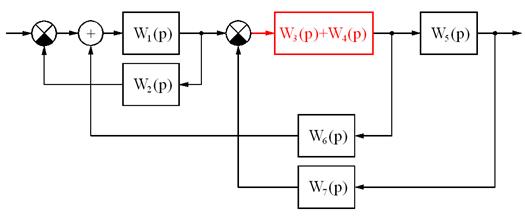
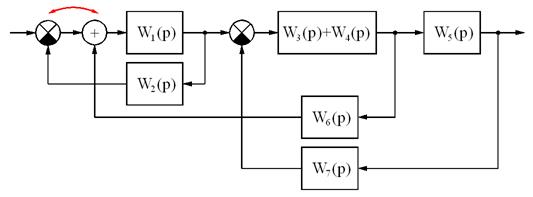
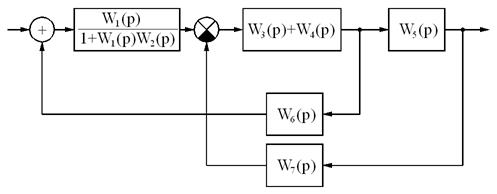
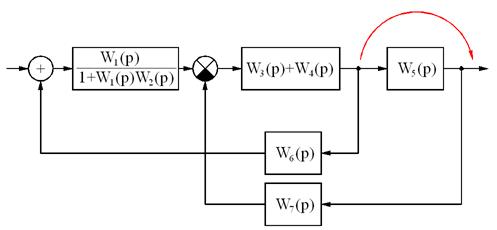
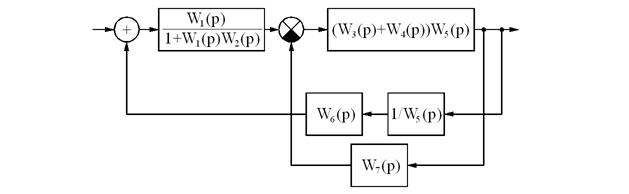
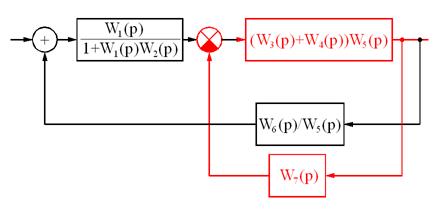
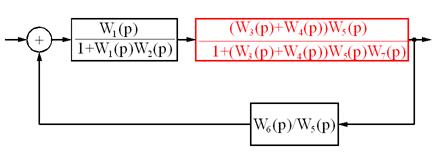
Итоговая передаточная функция:
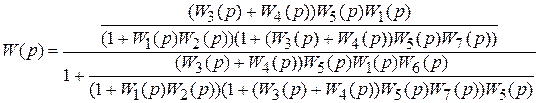
или после преобразования
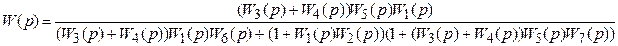
Литература: [1, c. 89 – 149], [4, c. 56 – 113]
АНАЛИЗ КАЧЕСТВА САР
