Фазо-частотных характеристик цепи

Входные и передаточные функции цепи представляют собой рациональные функции переменной S

где M(s), N(s) – полиномы. При подстановке получим

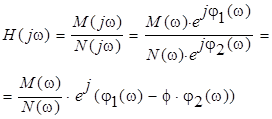(11)

Зависимость модуля 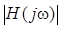от ω, т.е.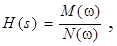

называется амплитудно–частотной характеристикой цепи, а 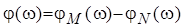– фазо–частотной характеристикой цепи.

Определение спектров входного и выходного сигналов в виде одиночных импульсов

Спектр импульсного сигнала находят по изображению сигнала, используя связь преобразований Лапласа и Фурье. Для одиночного импульса напряжения u_I(t), имеющего изображение U₁(s), комплексный спектр составит

Модуль функции U₁(jω) определяет амплитудный спектр A₁(ω), а аргумент U₁(jω)-фазовый спектр φ₁(ω)

Так, например, для сигнала в виде прямоугольного импульса получим комплексный спектр

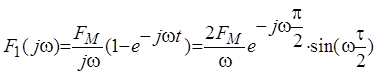
Амплитудный спектр

При A₁=0 , где k = ±1,±2…

Фазовый спектр

Графики амплитудного и фазового спектра показаны на рис.8.

Рис.8

Спектр выходного сигнала определяется с учетом частотных характеристик цепи.

или ,

где A₁(w), - амплитудный и фазовый спектр выходного сигнала соответственно.

Откуда следует, что

,

.

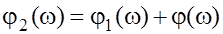При построении графиков спектров их целесообразно изобразить на одном рисунке.

Расчет вынужденного режима при несинусоидальном периодическом воздействии

При рассмотрении этого режима сигнал на входе цепи представляют в виде периодической последовательности заданных в условии задачи импульсов. Период Т принимают равным Т-nτ, где τ- длительность импульса, а величина n и форма импульса указаны в таблице вариантов.

Для нахождения комплексных амплитуд Аk периодического сигнала f1(t) можно использовать соотношение, связывающее величины Аk с изображением одиночных импульсов F1(s), совпадающее с периодической функцией f1 (t) в пределах периода [0;T].

Известно, что комплексные амплитуды определяются соотношением

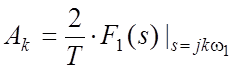
где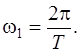

Очевидно, что связь А_k с комплексным спектром будет аналогичной:

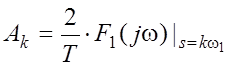
определим комплексные амплитуды для периодической последовательности прямоугольных импульсов длительностью

При k = 0 A = tF

,

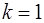
k = 2 ,

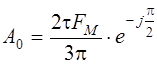и т. д.

Переходя во временную область, получим ряд Фурье в виде

.

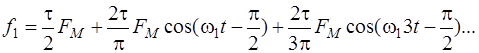По полученным выражениям комплексных амплитуд могут быть построены амплитудный и фазовый спектр периодического сигнала.

Для нахождения действующего значения напряжения используют формулу [8]

Для получения комплексного спектра выходного сигнала используют соотношение :

.

Анализ цепи на ЭВМ

Анализ цепи необходимо провести, используя различные прикладные программы: MathCad [2], Electronic WorkBench [3], MATLAB [4,7]. Целью этого раздела является ознакомление с методами приближенного определения реакций цепи и составления полученных результатов с аналитическими расчетами, полученными в предыдущих разделах.

Для проведения анализа в среде MathCad необходимо определить матрицы уравнений состояний. Для этого разработана программа MPS, алгоритм работы программы изложен в [1]. Работа с программой осуществляется в диалоговом режиме. Рассмотрим её работу на примере схемы рис.2. Зададимся параметрами этой цепи: R1=2Ом, R2=1Ом, С1=1Ф, С2=2Ф, L=1Гн, U =1В.

Перед работой с ЭВМ необходимо пронумеровать узлы схемы. Каждый элемент задания параметрам, узлом входа и выхода.

Пример диалога:

Количество элементов R?

2 < >

Параметры и узлы входа и выхода первого элемента R.

2 1 2 < >

Параметры и узлы входа и выхода второго элемента R.

1 3 4 < >

Количество элементов С?

2 < >

Параметры и узлы входа и выхода первого элемента С.

1 2 4 < >

Параметры и узлы входа и выхода второго элемента C.

2 3 4 < >

Количество элементов L?

1 < >

Параметры и узлы входа и выхода первого элемента L.

1 2 3 < >

Количество элементов I?

0 < >17

Количество элементов U?

1 < >

Параметры и узлы входа и выхода первого элемента U.

1 4 1 < >

Матрица А.

Матрица В.

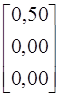
Выходные уравнения для токов через резисторы R1 и R2.

Матрица С.

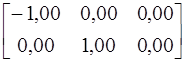
Для реакции y = i_R2 в матрицах C и D выбирают последние строки.

Имея описание цепи, с помощью уравнений состояний, легко осуществить численный расчет реакции схемы на различные воздействия, так что численное решение уравнений состояния сводилось к их численному интегрированию.

Рассмотрим уравнение (7). Чтобы перейти к численной схеме его решения, в простейшем случае можно воспользоваться методом Эйлера.

где h – шаг по времени, принимаемый постоянным.

Тогда уравнение (7) примет вид:

(7)

или интеграционная процедура

(12)

Очевидно, что выражение (12) необходимо дополнить начальными условиями:

x₀=0;

t₀=0.

Выражение (12) можно использовать как базовое для численного решения уравнений, описывающих цепь. Наиболее просто составить программу для решения дифференциальных уравнений, используя систему MathCad.

Для задания входного воздействия необходимо использовать функцию системы MathCad δ₁(t) – Хевисайда. Для получения функции δ(t) используют приближенное выражение

,

что соответствует узкому прямоугольному импульсу единичной площади.

Отметим, что при D, не равном нулю, невозможно получить точное значение импульсной характеристики вследствие наличия в ней слагаемого D×δ(t).

При D = 0 рекомендуется учитывать эту матрицу в конце расчета.

Образец программы с пояснениями представлен в Прил.1

Расчет спектральных характеристик и сигналов в системе MathCad осуществляется с помощью интегрирования функций комплексной переменной.

Зададим интеграл Фурье в виде

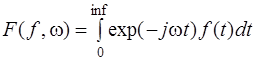
TOL=0.01

где inf = τ – длительность сигнала, TOL – точность интегрирования, задаваемая от площади сигнала, f(t) – представление сигнала в программе.

Так для прямоугольного сигнала

Пример выполнения программы представлен в приложении №2

В программе реализован контроль правильности полученных результатов с помощью обратного преобразования Фурье

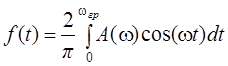
где ω_гр. – верхняя граница амплитудного спектра.

Расчет частотных характеристик цепи можно произвести в системе MathCad, используя

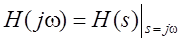
где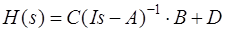

Амплитудно-частотная и фазо-частотная характеристики будут

A(ω)=|H(jω)|;

.

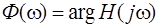Целесообразно сопоставить полученные результаты с результатами моделирования в системе Electronic WorkBench [3] с применением Боде-плоттера.

10. Рекомендации к выполнению и оформлению

Курсового расчета

Курсовую работу оформляют в виде пояснительной записки с титульным листом, на котором указывают министерство, институт, кафедру, наименование курсовой работы, исполнителя и фамилию преподавателя, а также место и год выполнения. На первом листе пояснительной записки должно быть оглавление, на втором – техническое задание; порядок расчета соответствует разделам данного методического руководства; в конце пояснительной записки следует привести заключение (краткие выводы по курсовой работе с анализом полученных результатов) и список использованной литературы.

Расчеты следует сопровождать ясными и краткими комментариями. Пояснительная записка должна иметь рубрикацию с выделением соответствующих разделов работы. К каждому разделу прилагаются листинги программ на ЭВМ с соответствующими результатами расчетов.

Работа выполняется на листах формата А4 в печатном виде.

Приложение 1.

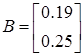
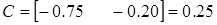– матрицы, определяющие цепь в пространстве состояний.

h : = 0.01 – шаг интегрирования

n : = 2000 – количество шагов

T : = 0.02 – параметр воздействия

i : = 0…n – 1 – начало цикла интегрирования

функция воздействия:

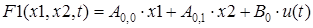
задание начальных условий:

,

численное интегрирование по методу Эйлера:

,

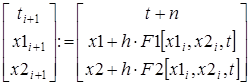определение реакции:

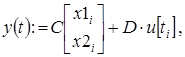
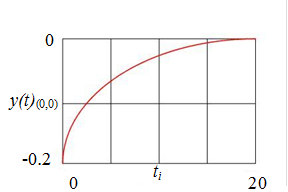
Приложение 2.

Преобразование Фурье .

inf : = 1 – верхняя граница интегрирования,

TOL : = 0.05 – точность интегрирования,

– задание комплексной единицы.

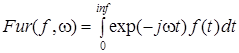
n : = 300

dw : = 0.1

k : = 0…n

W_k: = k dw

T : = 1

Форма сигнала:

,

,

,

.

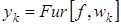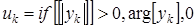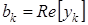Амплитудный спектр

Фазовый спектр

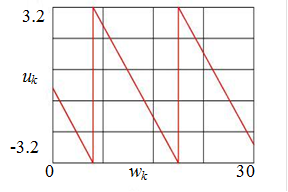
Рекомендуемая литература

1. Чуа Л. О. Машинный анализ электронных схем: алгоритмы и вычислительные методы / Л. О. Чуа, Лин Пен-Мин. – М.: Энергия, 1980. – 640 с.

2. Дьяконов В. П. Система MATCAD / В. П. Дьяконов. – М.: Радио и связь, 2001.

3. Электротехника и электроника в экспериментах и упражнениях. Практикум на Electronic WorkBench. Под общей ред. Д.И.Панфилова. М.:Додэка,- 1999- т.1, 304с.

4. .Новгородцев А.Б. Расчет электрических цепей в MATLAB:Учебный курс.-СПб.:ПИТЕР,-2004

5. Новгородцев А.Б. 30 лекций по теории электрических цепей.-СПб.: Политехника, 1995.-520с.

6. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники, 4-е изд.-СПб.:Питер,2003-т.1, 424с.

7. Дьяконов В.П., MATLAB 6. – СПб.: Питер, 2001.-592с.

8. Бычков Ю.А., Золотницкий В.М., Чернышев Э.П. Основы теории электрических цепей.-СПб.:Лань, 2004.