Повторные испытания. Формула Бернулли

Пусть проводится n независимых испытаний, в каждом из которых некоторое событие А может как появиться, так и не появиться. Пусть вероятность появления события А в одном испытании постоянна и равна p (вероятность непоявления события А равна q = 1– p).

При этих условиях вероятность того, что событие А при проведении n испытаний наступит ровно k раз определяется формулой Бернулли:

.

Число наступления события А в независимых испытаниях называется наивероятнейшим, если вероятность того, что событие А наступит в этих испытаниях раз, превышает (или не меньше) вероятности остальных исходов испытаний. Число определяется с помощью двойного неравенства:

Если – дробное число, то существует одно наивероятнейшее число .

Если – целое число, то существуют два наивероятнейших числа и .

Если – целое число, то .

Задача. Вероятность того, что изделие не пройдет контроля равна 0,125. Найти вероятность того, что среди 12 изделий не будет ни одного бракованного.

Решение. Обозначим событие А – «изделие не пройдет контроля». Проводится n = 12 независимых испытаний. Необходимо найти вероятность того, что событие А произойдет k = 0 раз (не будет ни одного изделия, не прошедшего контроля). Вероятность появления события А p = 0,125=1/8, непоявления – q = 0,875=7/8. По формуле Бернулли (17.1) получим:

.

Формула Пуассона

В случае, когда при возрастании n вероятность p появления интересующего события убывает, а — постоянное число (будем полагать, что a £ 10), то вероятность того, что событие А при проведении n испытаний наступит ровно k раз можно вычислить по формуле Пуассона:

.

Формула Пуассона является хорошим приближением формулы Бернулли в случае, когда вероятность события мала (p ® 0, ), а число испытаний n велико. Формулу Пуассона называют законом редких событий.

Потоком событий называется последовательность событий, которые наступают в случайные моменты времени.

Интенсивностью потока l называется среднее число событий, которое появляется в единицу времени.

Вероятность появления k событий простейшего потока за время t определяется формулой Пуассона:

.

Задача. С конвейера за сутки сходит 6 бракованных деталей. Конвейер работает в три смены. Определить вероятность того, что за смену не будет ни одной бракованной детали.

Решение. Интенсивность появления брака l = 6/24 = 0,25. Период времени t = 8 (ч.) – смена. Найдем вероятность того, что за смену не будет брака:

.

Дискретные случайные величины.

Числовые характеристики дискретных случайных величин.

Функция распределения

Случайной величиной называется величина, которая в результате испытания принимает любое наперед неизвестное значение из некоторого числового множества. Значение случайной величины зависит от многих случайных факторов, которые до опыта не могут быть учтены.

Случайная величина называется дискретной, если она принимает значения из некоторого фиксированного конечного или счетного множества. В этом случае значения случайной величины можно пронумеровать.

Законом распределения дискретной случайной величины называется соответствие между ее возможными значениями и их вероятностями. Закон распределения может быть задан аналитически, графически и таблично. Закон распределения в табличной форме имеет вид:

Х	х1	х2	…	xn
Р	р1	р2	…	pn

В первой строке таблицы содержатся возможные значения случайной величины Х, во второй — вероятности этих значений. При каждом испытании случайная величина Х может принять только одно значение, поэтому события Х = x₁, Х = x₂, …, Х = x_n образуют полную группу попарно несовместных событий, и, следовательно, .

Многоугольником(полигоном)распределения дискретной случайной величины называется графическое представление закона ее распределения. Для построения многоугольника распределения в прямоугольной декартовой системе координат надо последовательно соединить точки с координатами , где 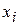— возможные значения случайной величины Х, — соответствующие вероятности (i = 1, 2, …, n).

Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех её возможных значений на их вероятности:

.

Дисперсией (рассеянием) D(X) дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

Дисперсию удобно вычислять по формуле:

.

Средним квадратическим отклонениемs(Х)дискретной случайной величины Х называется корень квадратный из дисперсии:

.

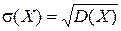Функцией распределения (интегральной функцией) случайной величины Х называется функция F(x), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее х:

.

Свойства функции распределения

1. Значения функции распределения 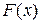принадлежит отрезку [0; 1]:

.

2. 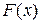— неубывающая функция, т.е. , если .

3. Если возможные значения случайной величины принадлежат интервалу (a, b), то при , при .

4. Вероятность того, что случайная величина Х примет значение, принадлежащее промежутку [a, b), равна приращению функции распределения на этом промежутке:

Задача. Дискретная случайная величина Х задана законом распределения:

Х
Р	0,2	0,1	0,4	0,3

1. Построить многоугольник распределения.

2. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

3. Найти функцию распределения случайной величины Х и построить ее график.

4. Найти вероятность того, что в результате испытания случайная величина Х примет значение из интервала [3; 6).

Решение. 1. Многоугольник распределения – ломаная, соединяющая точки с координатами . Для данной случайной величины многоугольник распределения выглядит следующим образом:

2. Найдем математическое ожидание М(Х).

Найдем дисперсию D(X).

Способ 1. Запишем закон распределения случайной величины :

	12,96	2,56	0,16	5,76
P	0,2	0,1	0,4	0,3

Используя формулу , получим: .

Способ 2. Используем формулу . Для этого запишем закон распределения случайной величины :

P	0,2	0,1	0,4	0,3

.

.

Найдем среднее квадратическое отклонение : .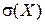

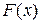3. По формуле . Найдем значения для разных интервалов значений переменной х:

при вероятность того, что случайная величина Х примет значение, меньшее х, равна (величина Х не принимает значения меньшие 1);

при (величина Х принимает одно значение, меньшее х, х = 1, его вероятность р = 0,2);

при (величина Х принимает два значения, меньших х, х₁ = 1 или х₂ = 3, вероятность суммы этих событий равна сумме вероятностей );

при (величина Х принимает три значения, меньших х, х₁=1, х₂ = 3 или х₃ = 5, вероятность суммы этих событий равна сумме вероятностей );

при (все значения, которые принимает случайная величина Х меньше х, это достоверное событие, вероятность его равна ).

Функция распределения случайной величины Х имеет вид:

,

Ее график выглядит следующим образом:

4. Вероятность того, что в результате испытания случайная величина Х примет значение из интервала [3; 6) равна:

.