Стоячие волны в длинных линиях
Как было показано выше, решение уравнений длинной линии можно представить в виде суммы прямой и обратной волн. В результате их наложения в цепях с распределенными параметрами возникают стоячие волны.
Рассмотрим два предельных случая: ХХ и КЗ в линии без потерь, когда поглощаемая приемником активная мощность равна нулю.
При ХХ на основании уравнений (17) и (18) имеем
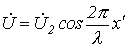и 
,
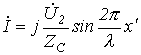откуда для мгновенных значений напряжения и тока можно записать
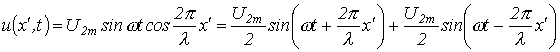 ; | (19) |
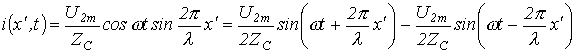 . | (20) |
Последние уравнения представляют собой уравнения стоячих волн, являющихся результатом наложения прямой и обратной волн с одинаковыми амплитудами.
При ХХ в соответствии с (19) и (20) в точках с координатами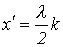 
, где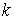 
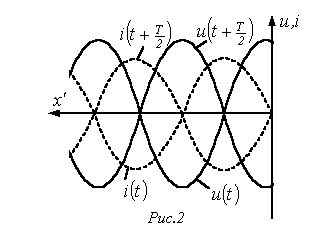
- целое число, имеют место максимумы напряжения, называемые пучностями,и нули тока, называемые узлами. В точках с координатами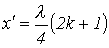 
пучности и узлы напряжения и тока меняются местами (см. рис. 2). Таким образом, узлы и пучности неподвижны, и пучности одной переменной совпадают с узлами другой и наоборот.
При КЗ на основании уравнений (17) и (18)
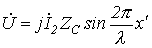и 
,
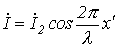откуда для мгновенных значений можно записать
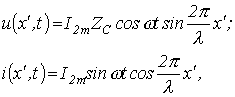
т.е. и в этом случае напряжение и ток представляют собой стоячие волны, причем по сравнению с режимом ХХ пучности и узлы напряжения и тока соответственно меняются местами.
Поскольку в узлах мощность тождественно равна нулю, стоячие волны в передаче энергии вдоль линии не участвуют. Ее передают только бегущие волны. Чем сильнее нагрузка отличается от согласованной, тем сильнее выражены обратные и, следовательно, стоячие волны. В рассмотренных предельных случаях ХХ и КЗ имеют место только стоячие волны, и мощность на нагрузке равна нулю.
Литература
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
- Что называется линией без искажений? Как соотносятся первичные параметры в такой линии?
- Запишите уравнения линии конечной длины для случаев, когда заданы ее входные напряжение и ток и когда выходные.
- Как определяются параметры цепи с распределенными параметрами?
- Что называется линией без потерь? Какими свойствами она обладает?
- При каких условиях в линии образуются стоячие волны?
- Определить напряжение и ток на входе трехфазной линии электропередачи длиной
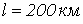, если 
, 
, 
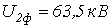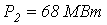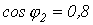. Параметры линии на фазу: 
, 
, 
, 
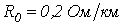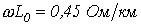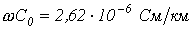. Определить КПД линии.
Ответ: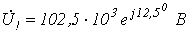 
; 
; 
.
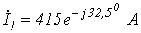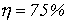- Определить входное сопротивление линии без потерь длиной в четверть волны, нагруженной на емкостную нагрузку
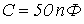при частоте 100 МГц. Волновое сопротивление 
.
Ответ: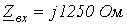 
.
- Однородная двухпроводная линия без искажений имеет волновое сопротивление , скорость распространения волны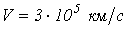
и затухание 1,5 Неп на 100 км. Определить первичные параметры линии, и также ее КПД при длине 
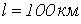и нагрузке, равной волновой.
Ответ: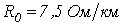 
; 
; 
; 
; 
.
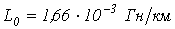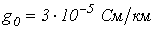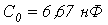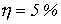- Линия без потерь нагружена на емкостное сопротивление, численно равное волновому.
, 
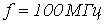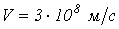. В конце линии 
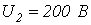. Найти 
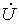на расстоянии 1м от конца линии.
Ответ: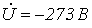 
.
- Линия без потерь длиной
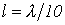разомкнута на конце. 
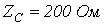, в начале линии 
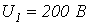. Найти 
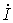в середине линии.
Ответ: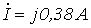 
.
Входным сопротивлением длинной линии (цепи с распределенными параметрами) называется такое сосредоточенное сопротивление, подключение которого вместо линии к зажимам источника не изменит режим работы последнего. В общем случае для линии с произвольной нагрузкой  для входного сопротивления можно записать
Полученное выражение показывает, что входное сопротивление является функцией параметров линии
Такой же величиной определяется входное сопротивление при При некоторых значениях длины линии ее входное сопротивление может оказаться чисто активным. Длину линии, при которой
Из (2) для режимов холостого хода (ХХ) и короткого замыкания (КЗ), т.е. случаев, когда потребляемая нагрузкой активная мощность равна нулю, соответственно получаем:
Исследование характера изменения В соответствии с (4) аналогичный характер, но со сдвигом на четверть волны, будет иметь зависимость
Точки, где Таким образом, изменяя длину линии без потерь, можно имитировать емкостное и индуктивное сопротивления любой величины. Поскольку длина волны Наши рекомендаци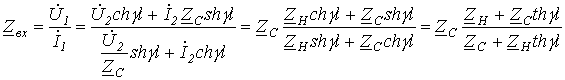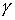и |
. 
и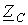 
, ее длины 
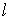и нагрузки 
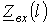, не является монотонной, а носит колебательный характер, обусловленный влиянием обратной (отраженной) волны. С ростом длины линии как прямая, так соответственно и отраженная волны затухают все сильнее. В результате влияние последней ослабевает и амплитуда колебаний функции 
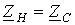, как было показано ранее, обратная волна отсутствует, что полностью соответствует выражению (1), которое при 
.
.
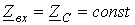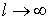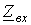вещественно, называют резонансной. Как и в цепи с сосредоточенными параметрами, резонанс наиболее ярко наблюдается при отсутствии потерь. Для линии без потерь на основании (1) можно записать
. 
; 
. 
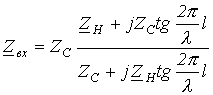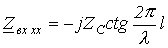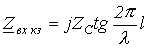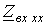в зависимости от длины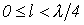 
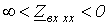и имеет емкостный характер, а при 
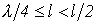- в пределах 
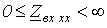и имеет индуктивный характер. Такое чередование продолжается и далее через отрезки длины линии, равные четверти длины волны (см. рис. 1,а).
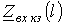при КЗ (см. рис. 1,б).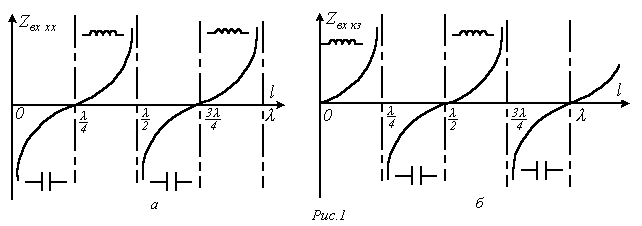
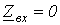, соответствуют резонансу напряжений, а точки, где 
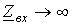, - резонансу токов.
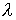есть функция частоты, то аналогичное изменение