Высшие гармоники в трехфазных цепях
Напряжения трехфазных источников энергии часто бывают существенно несинусоидальными (строго говоря, они несинусоидальны всегда). При этом напряжения на фазах В и С повторяют несинусоидальную кривую  напряжения на фазе А со сдвигом на треть периода Т основной гармоники:
напряжения на фазе А со сдвигом на треть периода Т основной гармоники:
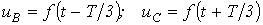 .
.
Пусть для фазы А к-я гармоника напряжения
 .
.
Тогда с учетом, что  , для к-х гармонических напряжений фаз В и С соответственно можно записать:
, для к-х гармонических напряжений фаз В и С соответственно можно записать:
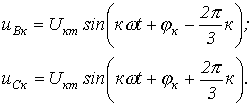
Всю совокупность гармоник к от 0 до 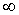 можно распределить по трем группам:
можно распределить по трем группам:
1. 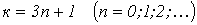 - гармоники данной группы образуют симметричные системы напряжений, последовательность которых соответствует последовательности фаз первой гармоники, т.е. они образуют симметричные системы напряжений прямой последовательности.
- гармоники данной группы образуют симметричные системы напряжений, последовательность которых соответствует последовательности фаз первой гармоники, т.е. они образуют симметричные системы напряжений прямой последовательности.
Действительно,

и
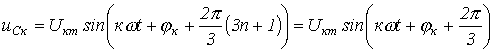 .
.
2.  . Для этих гармоник имеют место соотношения:
. Для этих гармоник имеют место соотношения:

т.е. гармоники данной группы образуют симметричные системы напряжений обратной последовательности.
3.  . Для этих гармоник справедливо
. Для этих гармоник справедливо

Таким образом, векторы напряжений данной группы во всех фазах в любой момент времени имеют одинаковые модули и направления, т.е. эти гармоники образуют системы нулевой последовательности.
Рассмотрим особенности работы трехфазных систем, обусловленные наличием гармоник, кратных трем.
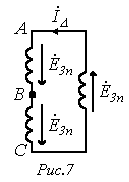 1. Если фазы генератора соединены в треугольник, то при несинусоидальных фазных ЭДС сумма ЭДС, действующих в контуре (см. рис. 7) не равна нулю, а определяется гармониками, кратными трем. Эти гармоники вызывают в замкнутом треугольнике генератора ток, даже когда его внешняя цепь разомкнута:
1. Если фазы генератора соединены в треугольник, то при несинусоидальных фазных ЭДС сумма ЭДС, действующих в контуре (см. рис. 7) не равна нулю, а определяется гармониками, кратными трем. Эти гармоники вызывают в замкнутом треугольнике генератора ток, даже когда его внешняя цепь разомкнута:
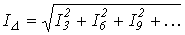 ,
,
где  , а
, а  - сопротивление фазы генератора для i-й гармоники, кратной трем.
- сопротивление фазы генератора для i-й гармоники, кратной трем.
2. Если фазы генератора соединить в открытый треугольник (см. рис. 8), то на зажимах 1-2 будет иметь место напряжение, определяемое суммой ЭДС гармоник, кратных трем:
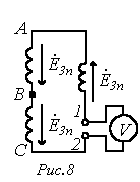
 .
.
Таким образом, показание вольтметра в цепи на рис. 8
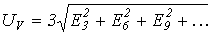 .
.
3. Независимо от способа соединения – в звезду или в треугольник – линейные напряжения не содержат гармоник, кратных трем.
При соединении в звезду это объясняется тем, что гармоники, кратные трем, как указывалось, образуют нулевую последовательность, ввиду чего исчезают из линейных напряжений, равных разности фазных.
При соединении в треугольник составляющие фазных ЭДС, кратные трем, не выявляются в линейных (фазных) напряжениях, так как компенсируются падениями напряжений на собственных сопротивлениях фаз генератора.
Таким образом, при соединении в треугольник напряжение генератора
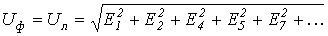
и ток
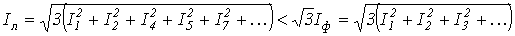 .
.
В свою очередь при соединении в звезду
 .
.
4. При симметричной нагрузке ток в нейтральном проводе определяется гармоническими, кратными трем, поскольку они образуют нулевую последовательность:
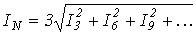 .
.
5. При соединении в звезду и отсутствии нейтрального провода фазные токи нагрузки не содержат гармоник, кратных трем (в соответствии с первым законом Кирхгофа сумма токов равна нулю, что невозможно при наличии этих гармоник). Соответственно нет этих гармоник и в фазных напряжениях нагрузки, связанных с токами законом Ома. Таким образом, при наличии гармоник, кратных трем, в фазных напряжениях генератора напряжение смещения нейтрали в симметричном режиме определяется этими гармониками
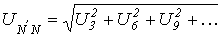 .
.
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- Какой характер: монотонный или колебательный – будет иметь зависимость действующего значения тока от величины индуктивности в цепи на рис. 1 при ее изменении от нуля до бесконечности?
- Почему на практике сигнал, пропорциональный току, получают с использованием резистивных шунтов?
- Какие гармоники и почему определяют характерные особенности режимов работы трехфазных цепей?
- Какие гармоники отсутствуют в линейных напряжениях и токах?
- Почему при несинусоидальных источниках питания, соединенных в треугольник, действующее значение фазной ЭДС может быть больше действующего значения фазного напряжения?
- При соединении трехфазного генератора и симметричной нагрузки по схеме «звезда-звезда» без нейтрального провода фазная ЭДС источника определяется выражением
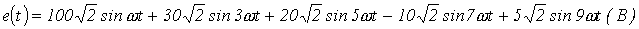
Определить действующие значения линейного напряжения, фазных напряжений генератора и приемника, а также напряжение смещения нейтрали.
Ответ: 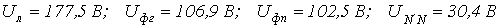 .
.
- В предыдущей задаче нейтральные точки генератора и приемника соединены проводом с нулевым сопротивлением.
Определить ток в нейтральном проводе, если сопротивление фазы нагрузки R=10 Ом.
Ответ: 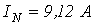 .
.
- При соединении трехфазного генератора и симметричной нагрузки по схеме «треугольник-треугольник» фазная ЭДС источника содержит первую и третью гармоники с амплитудами
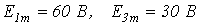 . Сопротивление нагрузки для первой гармоники
. Сопротивление нагрузки для первой гармоники 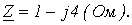
Определить действующее значение линейного тока.
Ответ: 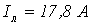 .
.
Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:
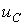 на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение. Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая. на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение. Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.  Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1. Составление характеристического уравнения по методу входного сопротивления заключается в следующем: записывается входное сопротивление цепи на переменном токе; jw заменяется на оператор р; полученное выражение Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1. Составление характеристического уравнения по методу входного сопротивления заключается в следующем: записывается входное сопротивление цепи на переменном токе; jw заменяется на оператор р; полученное выражение 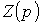 приравнивается к нулю. Уравнение приравнивается к нулю. Уравнение 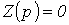 совпадает с характеристическим. Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание. Для цепи на рис. 1 относительно зажимов источника совпадает с характеристическим. Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание. Для цепи на рис. 1 относительно зажимов источника 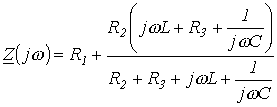 . Заменив jw на р и приравняв полученное выражение к нулю, запишем . Заменив jw на р и приравняв полученное выражение к нулю, запишем 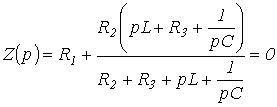 или или
При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов. Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид
Отсюда выражение для главного определителя этой системы
Приравняв D к нулю, получим результат, аналогичный (1). Наши рекомендации
|

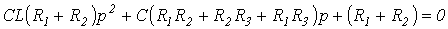 .
. 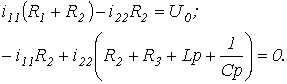
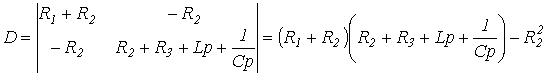 .
.