Воздушный (линейный) трансформатор
Одним из важнейших элементов электрических цепей является трансформатор, служащий для преобразования величин токов и напряжений. В простейшем случае трансформатор состоит из двух гальванически несвязанных и неподвижных катушек без ферромагнитного сердечника. Такой трансформатор называется воздушным. Он является линейным. Наличие ферромагнитного сердечника обусловило бы нелинейные свойства трансформатора.
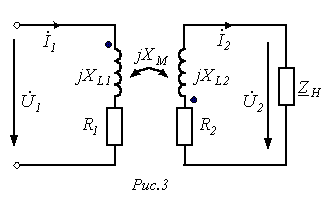 На рис. 3 представлена схема замещения трансформатора, первичная обмотка которого включена на напряжение U1, а от вторичной обмотки получает питание приемник с сопротивлением
На рис. 3 представлена схема замещения трансформатора, первичная обмотка которого включена на напряжение U1, а от вторичной обмотки получает питание приемник с сопротивлением  .
.
В трансформаторе энергия из первичной цепи передается во вторичную посредством магнитного поля. Если в первичной цепи под действием напряжения источника возникает переменный ток, то во вторичной цепи за счет магнитной связи катушек индуцируется ЭДС, вызывающая протекание тока в нагрузке.
По второму закону Кирхгофа для первичной и вторичной цепей трансформатора можно записать
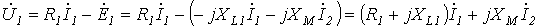 ;
;
 .
.
Таким образом, уравнения воздушного трансформатора имеют вид:
 ; ; | (11) |
 , . , . | (12) |
где 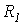 и
и 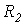 - активные сопротивления обмоток;
- активные сопротивления обмоток;  .
.
Если уравнения (11) и (12) решить относительно  , предварительно подставив в (12)
, предварительно подставив в (12)  и обозначив
и обозначив 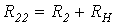 ;
;  , то получим
, то получим
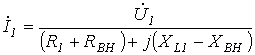 , , | (13) |
где  ;
;  - вносимые активное и реактивное сопротивления.
- вносимые активное и реактивное сопротивления.
Таким образом, согласно (13) воздушный трансформатор со стороны первичной обмотки может рассматриваться как двухполюсник с сопротивлением  .
.
 Баланс мощностей в цепях с индуктивно связанными элементами
Баланс мощностей в цепях с индуктивно связанными элементами
Пусть имеем схему по рис. 4, где А – некоторый активный четырехполюсник. Для данной цепи можно записать
 ;
;
 .
.
Обозначим токи  и
и 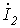 как:
как:  ;
;  .
.
Тогда для комплексов полных мощностей первой и второй ветвей соответственно можно записать:
 ;
;
 .
.
Рассмотрим в этих уравнениях члены со взаимной индуктивностью:
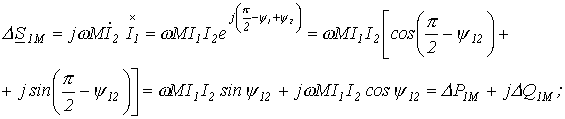 | (14) |
 . . | (15) |
где 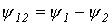 .
.
Из (14) и (15) вытекает, что
 ; ; | (16) |
 . . | (17) |
Соотношение (16) показывает, что активная мощность передается от первой катушки ко второй. При этом суммарная реактивная мощность, обусловленная взаимной индукцией, равна нулю, т.к.  . Это означает, что на общий баланс активной мощности цепи индуктивно связанные элементы не влияют.
. Это означает, что на общий баланс активной мощности цепи индуктивно связанные элементы не влияют.
Суммарная реактивная мощность, обусловленная взаимоиндукцией, равна
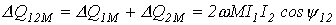 .
.
Таким образом, общее уравнение баланса мощностей с учетом индуктивно связанных элементов имеет вид
 , , | (18) |
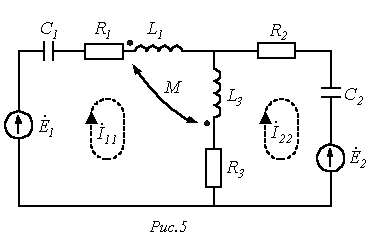 где знак “+” ставится при согласном включении катушек, а “-” – при встречном.
где знак “+” ставится при согласном включении катушек, а “-” – при встречном.
Расчет разветвленных цепей при наличии взаимной индуктивности может быть осуществлен путем составления уравнений по законам Кирхгофа или методом контурных токов. Непосредственное применение метода узловых потенциалов для расчета таких цепей неприемлемо, поскольку в этом случае ток в ветви зависит также от токов других ветвей, которые наводят ЭДС взаимной индукции.
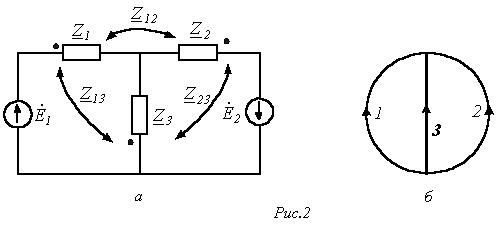
В качестве примера расчета цепей с индуктивно связанными элементами составим контурные уравнения для цепи на рис. 5:
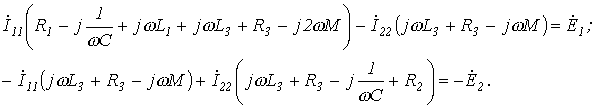
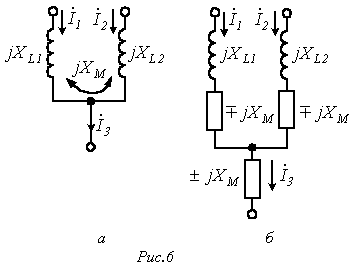 Чтобы обойти указанное выше ограничение в отношении применения метода узловых потенциалов для расчета рассматриваемых схем можно использовать эквивалентные преобразования, которые иллюстрируют схемы на рис. 6, где цепь на рис. 6,б эквивалентна цепи на рис. 6,а. При этом верхние знаки ставятся при согласном включении катушек, а нижние – при встречном.
Чтобы обойти указанное выше ограничение в отношении применения метода узловых потенциалов для расчета рассматриваемых схем можно использовать эквивалентные преобразования, которые иллюстрируют схемы на рис. 6, где цепь на рис. 6,б эквивалентна цепи на рис. 6,а. При этом верхние знаки ставятся при согласном включении катушек, а нижние – при встречном.
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А. Ионкин, А.В.Нетушил, С.В.Страхов. –5-еизд.,перераб.–М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какие элементы называются индуктивно связанными?
- Что такое коэффициент связи, и в каких пределах он изменяется?
- Что такое воздушный трансформатор? Почему он называется линейным?
- Запишите уравнения воздушного трансформатора, нарисуйте его схему замещения.
- Как влияют индуктивно связанные элементы на баланс мощностей?
- Какие методы расчета можно использовать для анализа цепей с индуктивно связанными элементами?
- Записать уравнения для расчета цепи на рис. 5, используя законы Кирхгофа.
- Записать контурные уравнения для цепи на рис. 5, используя эквивалентную замену индуктивных связей.
- С использованием эквивалентной замены индуктивных связей записать узловые уравнения для цепи на рис. 5.
- Рассчитать входное сопротивление на рис. 3, если
 ;
; 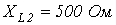 ;
; 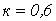 ;
; 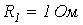 ;
; 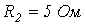 ;
; 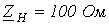 .
.
Ответ:  .
.
Матрицы сопротивлений и проводимостей для цепей со взаимной индукцией Как было показано ранее (см. лекцию N 6 ), для схем, не содержащих индуктивно связанные элементы, матрицы сопротивлений и проводимостей ветвей являются диагональными, т.е. все их элементы, за исключением стоящих на главной диагонали, равны нулю. В общем случае разветвленной цепи со взаимной индукцией матрица сопротивлений ветвей имеет вид Z  . Здесь элементы главной диагонали . Здесь элементы главной диагонали  , , 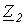 ,… ,… 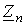 - комплексные сопротивления ветвей схемы; элементы вне главной диагонали - комплексные сопротивления ветвей схемы; элементы вне главной диагонали 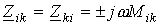 - комплексные сопротивления индуктивной связи i- й и k – й ветвей (знак “+” ставится при одинаковой ориентации ветвей относительно одноименных зажимов, в противном случае ставится знак “-”). Матрица проводимостей ветвей в цепях со взаимной индукцией определяется согласно Y = Z –1 . Зная матрицы и Y , можно составить контурные уравнения, а также узловые, т.е. в матричной форме метод узловых потенциалов распространяется на анализ цепей с индуктивно связанными элементами. Следует отметить, что обычно не все ветви схемы индуктивно связаны между собой. В этом случае с помощью соответствующей нумерации ветвей графа матрице Z целесообразно придать квазидиагональную форму Z - комплексные сопротивления индуктивной связи i- й и k – й ветвей (знак “+” ставится при одинаковой ориентации ветвей относительно одноименных зажимов, в противном случае ставится знак “-”). Матрица проводимостей ветвей в цепях со взаимной индукцией определяется согласно Y = Z –1 . Зная матрицы и Y , можно составить контурные уравнения, а также узловые, т.е. в матричной форме метод узловых потенциалов распространяется на анализ цепей с индуктивно связанными элементами. Следует отметить, что обычно не все ветви схемы индуктивно связаны между собой. В этом случае с помощью соответствующей нумерации ветвей графа матрице Z целесообразно придать квазидиагональную форму Z  , что облегчает ее обращение, поскольку Y , что облегчает ее обращение, поскольку Y 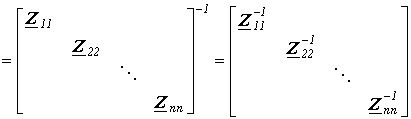 , где подматрицы , где подматрицы  могут быть квадратными диагональными или недиагональными. В качестве примера составим матрицы Z иYдля схемы на рис. 1,а, граф которой приведен на рис. 1,б. могут быть квадратными диагональными или недиагональными. В качестве примера составим матрицы Z иYдля схемы на рис. 1,а, граф которой приведен на рис. 1,б. 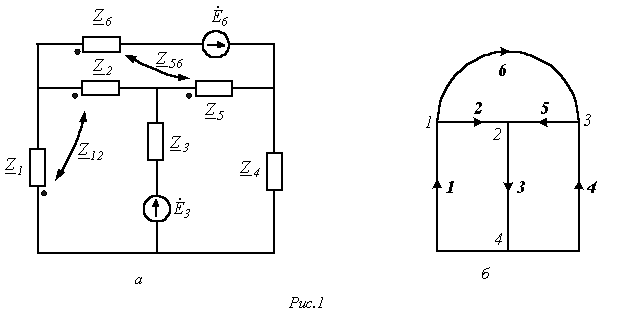 Для принятой нумерации ветвей матрица сопротивлений ветвей Z Для принятой нумерации ветвей матрица сопротивлений ветвей Z  . В этой матрице можно выделить три подматрицы, обращая которые, получим . В этой матрице можно выделить три подматрицы, обращая которые, получим
Таким образом, матрица проводимостей ветвей Y Отметим, что при принятой ориентации ветвей
Решение 1. Для заданной цепи составим граф (см. рис. 2,б), выделив в нем дерево, образованное ветвью 3. Тогда матрица главных контуров имеет вид В 2. Запишем матрицу сопротивлений ветвей с учетом их принятой ориентации Z 3. Определим матрицу контурных сопротивлений Zk=BZBT
4. Запишем столбцовую матрицу контурных ЭДС
5. Подставив найденные выражения в
Наши рекомендации
|

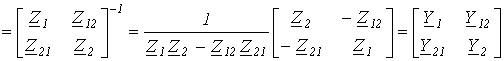 ;
;  ;
;  .
.  .
.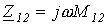 и
и  .
.
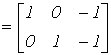 .
.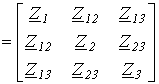 .
.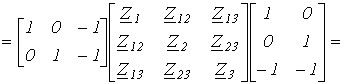


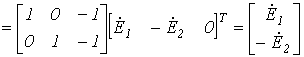 .
. , окончательно получим
, окончательно получим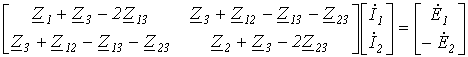 .
.