В силу следствия достаточно найти решение уравнения

,

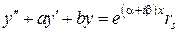но последнее было уже рассмотрено. Из этого следует, что его решение нужно искать в виде

,

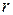– с неопределенными комплексными коэффициентами, – кратность 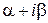в характеристическом уравнении.

На основании теоремы о наложении решений и следствия из вспомогательной теоремы,

,

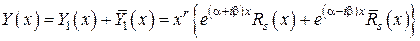где сопряжен с .

Снова используем формулы Эйлера:

,

.

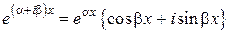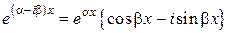Приводим 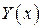к виду

, (**)

где 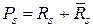, 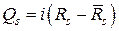– многочлены с вещественными коэффициентами.

Замечание.

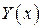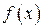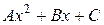При использовании (**) надо помнить, что вид подобен виду , но является более полным. Так, если , то в (**) мы должны брать , если 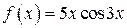, то в (**) следует взять , и если , то в (**) возьмем , и т. д.

Пример.

,

, , , ,

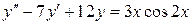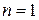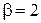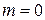, так как 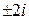не корень характеристического уравнения,

,

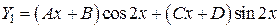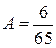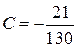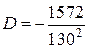, , , , и т. д.

9.4.3. Линейные дифференциальные уравнения, приводящиеся к урав­нениям с постоянными коэффициентами

Теорема.

Линейное дифференциальное уравнение преобразуется снова в линейное дифференциальное уравнение при всяком линейном преобразовании неизвестной функции и любом преобразовании аргумента (и только при таких преобразованиях).

Доказательство.

В уравнении

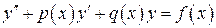
положим 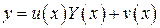, где 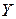– новая искомая функция, а 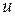и – известные функции. Тогда

,

,

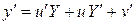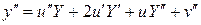и исходное уравнение преобразуется к виду

,

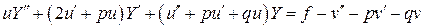и это уравнение снова является линейным, так как все коэффициенты и правая часть есть функции только 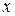. отметим, что входит только в правую часть.

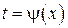Положим, что , тогда и

, .

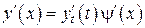Подставляя эти значения, получим опять линейное уравнение:

,

заменяя 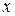на найдем, что все коэффициенты и правая часть есть функции только 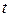. На этом доказательство первой части закончено.

Предположим теперь, что 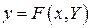. Тогда

, .

Подставляя 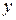, 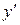и 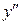в исходное уравнение, получим в общем случае нелинейное уравнение

. (*)

Чтобы (*) было линейным, нужно, чтобы 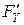и 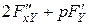не зависели от 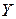, , а содержало 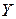лишь в первой степени или было функцией только от 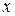. Выполнение этих требований превращает 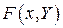в линейную функцию. Если

,

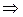
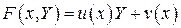и тогда не зависит от 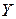, а . При этом

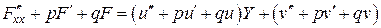
есть функция от 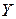в первой степени. Таким образом, теорема доказана.

Очевидно, что для преобразования линейного дифференциального уравнения с переменными коэффициентами в линйое дифференциальное уравнение с постоянными коэффициентами достаточно рассмотреть соответствующее однородное уравнение.

Согласно теореме, сохранение линейности возможно только в двух случаях: при линейном преобразовании функции 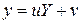( , так как она не входит в коэффициенты в левой части) и при произвольном преобразовании .

Теперь выведем условия, налагаемые на 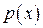и линейного дифференциального уравнения 2-го порядка, при которых это уравнение может быть приведено к линейному дифференциальному уравнению 2-го порядка с постоянными коэффициентами с помощью преобразования или .

Необходимое и достаточное условие для преобразования .

Итак, пусть дано уравнение

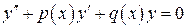(1)

и подстановка , тогда

,

,

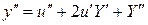подставляя в уравнение, получим:

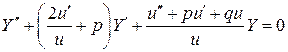, (2)

и потребуем, чтобы коэффициенты пр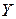и и были константами:

.

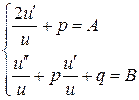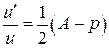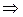
Тогда . Отсюда или

или

.

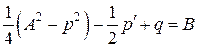Последнее равенство можно записать, как

, где . (3)

(3) и есть условие приводимости (1) к (2), в котором коэффициенты являются постоянными.

Найдем теперь , с помощью которой это приведение выполняется:

.

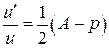
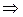
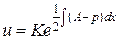Положим и , тогда и

.

Таким образом, преобразование выполняется, если выполнено (3).

Пример.

.

Условие (3) выполняется и 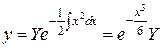приводит к уравнению

.

Необходимое и достаточное условие для преобразования .

Пусть 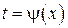, тогда

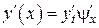и

. ( )

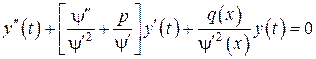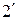Далее,

Из (*), считая , имеем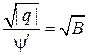

.

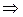
Кроме того, 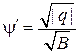. Подставляя эти результаты в (**), получим:

или ,

. ( )

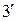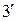( ) и есть искомое условие.

Найдем теперь 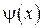. Из (*):

,

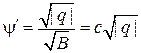
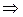
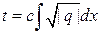где , а 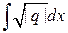– одна из первообразных от .

Таким образом, если выполняется ( 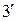), то (1) можно привести к уравнению с постоянными коэффициентами с помощью преобразования .

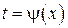Пример. Рассмотрим уравнение Эйлера

,

здесь 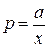, , 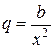, 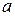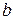– 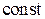, тогда или – нужная подстановка.