Неравенство П. Л. Чебышёва и законы больших чисел

Неравенство Чебышёва.

 Пусть случайная величина X такова, что математическое ожидание её квад-
рата существует и конечно: M(X²)<+¥.

 Тогда для любого e>0 справедливо неравенство:

             P{|X|³e}£ .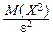

Доказательство. ƒ Введём случайную величину Y:

Y=

0, если |X|<e,
e², если |X|³e.

Это дискретная случайная величина. Её закон распределения даётся двумя вероятностями:

P{Y=0}=P{|X|<e},
P{Y=e²}=P{|X|³e};

её математическое ожидание равно: MY=e²P{|X|³e}.

Легко проверить, что Y£X². В самом деле, если Y=0, то неравенство очевидно; если Y=e², то при этом |X|³e Û X²³e². Отсюда: MY£M(X²), что можно переписать в виде:

P{|X|³e}£ . ‚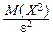

Неравенство Чебышёва записывают и в других формах. Например, применим его к случайной величине X-MX, в предположении, что существует дисперсия DX:

P{|X-MX|³e}£ = .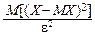

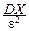Для противоположного события:

P{|X-MX|<e}³1- .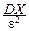

Применим неравенство Чебышёва в последней форме к среднему арифметическому 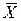попарно некоррелированных случайных величин X₁, X₂, ¼ , X_nc одинаковыми математическими ожиданиями MX_i=a и одинаковыми дисперсиями DX_i=s²:

1³P{| 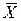-a|<e}³1- 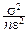, "e>0.

Перейдём здесь к пределу при n®+¥:

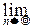P{| 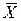-a|<e}=1, "e>0.

Мы получили так называемый закон больших чисел в форме Чебышёва.

  Закон больших чисел в форме Чебышёва

  Среднее арифметическое 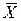отличается от истинного среднего значения
a меньше сколь угодно малого e>0 при достаточно большом числе наблюде-
ний с вероятностью, сколь угодно близкой к единице.

  Это утверждение кратко записывается так: 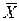 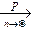a – и читается: " 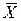схо-
дится по вероятности к a."

В частности, закон больших чисел Чебышёва действует в схеме повторных независимых равноточных измерений без систематической погрешности любой физической величины a и оправдывает нашу интуитивную веру в среднее арифметическое 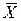как хорошее приближение для a. Мы получаем уверенность в том, что при достаточно большом числе измерений мы будем знать истинное значение измеряемой величины a сколь угодно точно со сколь угодно большой вероятностью. Однако закон больших чисел указывает лишь очень грубо, сколько наблюдений достаточно выполнить, чтобы добиться заданной точности: если мы хотим, чтобы P{| 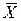-a|<e}³1-d, достаточно произвести n³  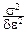наблюдений.

Из закона больших чисел Чебышёва следует закон больших чисел Бернулли.

  Закон больших чисел в форме Бернулли.

  Относительная частота 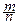  события A сходится по вероятности к вероят-
ности p события A: 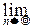 P{| 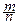-p|<e}=1 для "e>0.

Действительно, пусть проведено n независимых опытов, в которых событие A произошло m раз. Введём случайные величины

Xi=

1, если событие A_iпроизошло,
0, если событие A_iне произошло.

Это дискретные случайные величины, причём:

MX_i=1×p+0×(1-p)=p, MX_i²=1²×p+0²×(1-p)=p, DX_i=M(X_i²)-(MX_i)²=p-p²=pq,
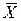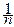= (X_i+X₂+¼+X_n)= .

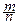Выполнены условия закона больших чисел Чебышёва, в котором a=p, s²=pq. Поэтому: 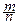 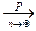p.

Закон больших чисел в форме Бернулли даёт обоснование нашей интуитивной веры в относительную частоту как приближение для вероятности: как бы ни было мало e>0, для достаточно большого числа наблюдений n относительная частота 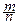события A бу­дет отличаться от его вероятности p меньше этого e с вероятностью, как угодно близкой к единице.

Возможно нам хотелось бы большего, а именно: 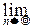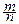=p. Но так много теория вероятностей дать не может. И это по существу! Например, при бросании монеты ничто не мешает ей всё время выпадать решкой, а для подобной серии испытаний относительная частота гербов равна нулю. Нетрудно также построить серию испытаний, для которой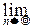 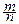  принимает любое заданное значение на отрезке [0, 1], либо не существует. Тем удивительнее усиленный закон больших чисел, доказанный Борелем.

  Усиленный закон больших чисел (Борель).

  Предел относительной частоты 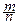  события A существует и равен вероят-
ности p этого события почти наверное: P{ 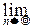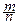=p}=1.

Связь относительной частоты и вероятности позволяет дать ещё одну мотивировку принятого в теории вероятностей определения математического ожидания и его толкования как среднего значения. Пусть дискретная случайная величина X с возможными значениями x_kи вероятностями p_kнаблюдается n раз независимым образом; пусть частота x_kравна m_k, Среднее арифметическое этих наблюдений равно

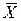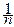
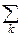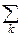= x_km_k= x_k .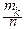

Можно думать, что истинное среднее мы получим, сделав бесконечно много наблюдений, а относительные частоты 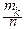при этом почти наверное будут равны вероятностям p_k. Это и даёт для истинного среднего выражение 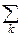x_kp_k, т. е. MX.