Лекции по теории вероятностей
Основные случайные величины
Любой сходящийся интеграл от неотрицательной функции порождает непрерывное распределение. Именно, если  j(x)dx=I, то роль плотности играет
j(x)dx=I, то роль плотности играет
|
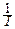 j(x), если xÎA,
j(x), если xÎA,0, если xÏA.
Любая конечная сумма или сходящийся ряд с неотрицательными слагаемыми порождает дискретное распределение. Именно: если 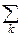 qk=S, то роль дискретных вероятностей играют pk=
qk=S, то роль дискретных вероятностей играют pk=  qk, а в качестве xkможно взять любые числа; наиболее простой выбор: xk=k.
qk, а в качестве xkможно взять любые числа; наиболее простой выбор: xk=k.
Рассмотрим конкретные примеры.
1°. Равномерное распределение. Его порождает интеграл  dx=b-a.
dx=b-a.
|
 , если xÎ[a, b],
, если xÎ[a, b],0, если xÏ[a, b].
Этот закон распределения будем обозначать R(a, b); числа a и b называются параметрами распределения. Тот факт, что случайная величина X равномерно распределена на отрезке [a, b], будем обозначать следующим образом: X~R(a, b).
В частности, плотность случайной величины X~R(0, 1) имеет наиболее простой вид:
|
0, если xÏ[0, 1].
Функция распределения такой случайной величины равна:
|
x, если 0£x£1,
1, если x>0.
Если мы наугад выбираем точку на отрезке [0, 1], то её абсцисса x является конкретным значением случайной величины X~R(0, 1). Слово ''наугад" имеет в теории вероятностей терминологическое значение и говорится с целью подчеркнуть, что соответствующая непрерывная случайная величина распределена равномерно, или дискретная случайная величина имеет конечное число N возможных равновероятных значений.
2°. Экспоненциальное распределение.
Его порождает интеграл  e-mxdx=
e-mxdx= 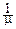 , m>0.
, m>0.
|
me-mx, если x³0,
0, если x<0,
|
1-me-mx, если x³0,
0, если x<0.
То обстоятельство, что случайная величина распределена по экспоненциальному закону, будем записывать так: X~Exp(m), m называется параметром распределения (m>0).
3°. Распределение Коши. Его порождает интеграл 
 dx=p.
dx=p.
Плотность вероятности: p(x)=  , -¥<x<+¥.
, -¥<x<+¥.
4°. Гамма-распределение. Его порождает интеграл, который определяет гамма-функцию: G(l)=  e-ttl-1dt, l>0. Выполним в этом интеграле замену переменной, положим: t=mx, m>0:
e-ttl-1dt, l>0. Выполним в этом интеграле замену переменной, положим: t=mx, m>0:
G(l)=ml  e-mxxl-1dx.
e-mxxl-1dx.
|
 xl-1e-mx, если x>0,
xl-1e-mx, если x>0,
0, если x£0.
Будем обозначать это распределение G(l, m), l и m – параметры распределения (l>0, m>0).
5°. Нормальное распределение. Его порождает интеграл Пуассона:
I= 
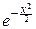 dx=
dx= 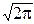 .
.
Докажем это равенство. Интеграл бы легко вычислялся, если бы подынтегральное выражение содержало множитель x. Такой множитель можно ввести под знак интеграла с помощью следующего остроумного приёма.
Запишем квадрат интеграла в следующем виде:
I2= 
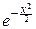 dx×
dx× 
 dy,
dy,
а теперь представим произведение интегралов как двойной интеграл:
I2= 

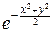 dxdy.
dxdy.
Перейдём в этом интеграле к полярным координатам. Положим: x=rcosj, y=
=rsinj, и ещё вспомним, что абсолютная величина якобиана при переходе от декартовых координат к полярным равна r. Заметим, наконец, что областью интегрирования двойного интеграла является вся плоскость, так что границы изменения переменных r и j, соответственно, таковы: rÎ[0; +¥), jÎ[0; 2p). Поэтому:
I2=  dj
dj 
 rdr.
rdr.
Теперь легко убедиться, что 
 rdr=1, а потому I2=2p.
rdr=1, а потому I2=2p.
Распределение с плотностью
p(x)= 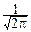
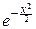 , xÎ(-¥; +¥)
, xÎ(-¥; +¥)
называется стандартным нормальным законом и обозначается N(0, 1).
Ему соответствует функция распределения:
F0(x)= 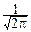
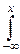
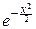 dx.
dx.
Обычно принято табулировать интеграл
F(x)= 
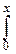
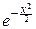 dx,
dx,
называемый интегралом ошибок или интегралом Лапласа. Функция распределения стандартного нормального закона просто выражается через этот интеграл:
F0(x)= 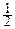 +
+ 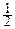 F(x).
F(x).
Если в интеграл Пуассона ввести параметры масштаба и сдвига с помощью замены переменной, заменив x на 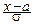 , то он примет вид:
, то он примет вид:


 dx=1.
dx=1.
Случайную величину с плотностью вероятности
p(x)= 
 , xÎ(-¥; +¥),
, xÎ(-¥; +¥),
называют нормально распределённой случайной величиной или просто нормальной. Соответствующий ей закон распределения обозначают N(a, s), a и s – параметры распределения (s>0, a – любое вещественное число).
График p(x) представлен на рис. 1.
     
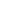
|
a – точка максимума p(x), его значение равно  . Так как площадь под кривой всегда равна единице, то чем меньше s, тем больше вероятности сосредоточивается вблизи максимума. Таким образом, устанавливаем вероятностный смысл параметров нормального закона: областью наиболее вероятных значений нормальной случайной величины является окрестность точки a, а s указывает на степень концентрации вероятности в окрестности точки a – чем меньше s, тем менее вероятны заметные отклонения X от a.
. Так как площадь под кривой всегда равна единице, то чем меньше s, тем больше вероятности сосредоточивается вблизи максимума. Таким образом, устанавливаем вероятностный смысл параметров нормального закона: областью наиболее вероятных значений нормальной случайной величины является окрестность точки a, а s указывает на степень концентрации вероятности в окрестности точки a – чем меньше s, тем менее вероятны заметные отклонения X от a.
Функцию распределения произвольного нормального закона легко выразить через интеграл Лапласа. Для этого нужно в выражении для функции распределения
F(x)= 
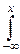
 dx
dx
выполнить замену переменной, положив 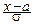 =y:
=y:
F(x)= 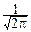
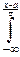
 dy=
dy= 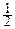 +
+ 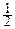 F(
F( 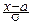 ).
).
6°. Геометрическое распределение. Его порождает геометрическая прогрессия: 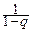 =
= 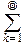 qk-1, 0<q<1.
qk-1, 0<q<1.
Соответствующая дискретная случайная величина имеет возможные значения xk=k, k=1, 2, ¼ с вероятностями pk=(1-q)qk-1. Обозначение геометрического распределения: G(q), q – параметр распределения (0<q<1).
7°. Пуассоновское распределение. Его порождает разложение в ряд показательной функции: el= 
 , l>0, которому отвечает дискретная случайная величина, принимающая целые неотрицательные значения xk=k, k=0, 1, 2, ¼ с вероятностями pk=
, l>0, которому отвечает дискретная случайная величина, принимающая целые неотрицательные значения xk=k, k=0, 1, 2, ¼ с вероятностями pk=  .
.
Будем обозначать это распределение через P(l), l – параметр распределения (l>0).
8°. Биномиальное распределение. Его порождает формула бинома Ньютона: (p+q)n= 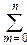
 pmqn-m.
pmqn-m.
Чтобы сумма вероятностей распределения pkравнялась единице и все они были положительными, возьмём p>0, q>0, p+q=1, т. е. q=1-p. Возможными значениями будем считать xk=k, k=0, 1, 2, ¼ , n, а их вероятностями – pk= 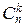 pkqn-k. Обозначим это распределение B(n, p), n и p – параметры распределения (0<p<1, nÎN, т. е. n – натуральное число).
pkqn-k. Обозначим это распределение B(n, p), n и p – параметры распределения (0<p<1, nÎN, т. е. n – натуральное число).
Биномиальная случайная величина появляется, например, в схеме Бернулли, называемой также схемой последовательных независимых испытаний. Состоит она в следующем: осуществляется некоторый комплекс условий, при котором мы имеем одно и только одно из двух событий: либо "успех", либо "неудачу", причём вероятность "успеха" равна p, вероятность "неудачи" равна q=
=1-p; эта попытка независимым образом повторяется n раз. Считая опытом все n попыток, можем считать элементарным событием опыта цепочку длины n, полученных в результате опыта "успехов" (У) и "неудач" (Н): УУУННУ
Н¼У.
Определим случайную величину X, задав её как число успехов в одном опыте. Событию {X=k} благоприятствуют те элементарные события, которые содержат "успех" ровно k раз, а "неудачу" – остальные n-k раз. Число таких благоприятствующих событию {X=k} элементарных событий, равно, очевидно, 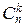 , а вероятности всех их одинаковы и по теореме умножения для независимых событий равны pkqn-k. Окончательно получаем: P{X=k}=
, а вероятности всех их одинаковы и по теореме умножения для независимых событий равны pkqn-k. Окончательно получаем: P{X=k}= 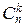 pkqn-k, а возможными значениями случайной величины X оказываются числа xk=k, k=
pkqn-k, а возможными значениями случайной величины X оказываются числа xk=k, k=
=0, 1, 2, ¼ n. Таким образом, число успехов X в схеме Бернулли – биномиальная случайная величина: X~B(n, p).
Пусть имеется вероятностное пространство (W, Å, P(×)) и рассматривается некоторое событие A. Обозначим его вероятность P(A)=p. Пусть испытание независимым образом повторяется n раз, причём событие A в этих n последовательных попытках наблюдалось k раз. Число k называется абсолютной частотой события A. Оно является конкретным значением случайной величины X, определённой на серии из n независимых испытаний. Ничто не мешает объявить событие A "успехом", а событие 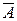 – "неудачей". Это превращает последовательность из n испытаний в схему Бернулли, а абсолютная частота события A оказывается распределённой по закону Бернулли.
– "неудачей". Это превращает последовательность из n испытаний в схему Бернулли, а абсолютная частота события A оказывается распределённой по закону Бернулли.
Геометрическое распределение также просто связано со схемой Бернулли: будем повторять попытку до появления первого "успеха". Элементарным событием в таком опыте является цепочка, у которой "успех" расположен только на последнем (k-м) месте, а на всех предыдущих местах (а их k-1) – только "неудачи": ННННН¼НУ. Свяжем с этим опытом случайную величину X – общее число попыток в опыте. Очевидно, значениями этой случайной величины могут быть xk=k, k=1, 2, 3, ¼ , а их вероятности pk=qk-1p, что и совпадает с геометрическим распределением G(p).
C– распределение
При y>0:
Fcn(y)=P{cn<y}=P{cn2<y2}= 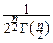
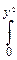
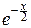
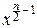 dx.
dx.
Отсюда:
pcn(y)= 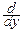 Fcn(y)=
Fcn(y)= 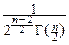
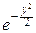 yn-1, при y>0, и pcn(y)º0, при y£0.
yn-1, при y>0, и pcn(y)º0, при y£0.
и, следовательно,
Fcn(x)= 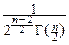
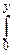
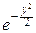 yn-1dy, при y>0 и Fcn(x)º0, при y£0.
yn-1dy, при y>0 и Fcn(x)º0, при y£0.
Распределение Стьюдента
Пусть даны две независимые случайные величины X~N(0, 1), и cn.
Определим случайную величину Tn равенством: Tn= 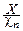 и найдём закон её распределения.
и найдём закон её распределения.
Совместная плотность вероятности двумерной случайной величины (X, cn) равна:
p(x, y)= 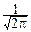
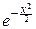
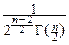
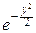 yn-1, для -¥<x<+¥, 0<y<+¥.
yn-1, для -¥<x<+¥, 0<y<+¥.
Функция распределения дроби Tn равна:
FTn(t)=P{Tn<t}=P{ 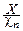 <t}=P{X<tcn}.
<t}=P{X<tcn}.
Неравенству X<tcn благоприятствуют точки, занимающие область, заштрихованную на Рис. 3:
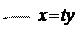
 |
Этой области досталась вероятность:
FTn(t)=P{Tn<t}=  dy
dy 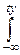 p(x, y)dx=
p(x, y)dx= 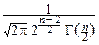
 dy
dy 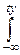
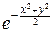 yn-1dx.
yn-1dx.
Отсюда находим плотность вероятности:
pTn(t)= 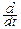 FTn(t)=
FTn(t)= 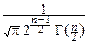
 yn-1
yn-1 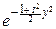 ydy.
ydy.
Отметим, что в интеграле t играет роль параметра и сделаем замену переменной:
u= 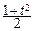 y2 Þ y=
y2 Þ y= 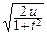 Þ dy=
Þ dy= 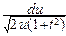 .
.
Имеем:
pTn(t)= 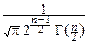 ×
× 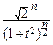 ×
× 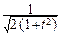
 e-u
e-u 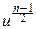 du
du
и, выражая интеграл через гамма-функцию, мы можем записать плотность распределения Стьюдента в следующем – окончательном виде:
pTn(t)= 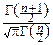 ×
× 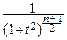 .
.
Отметим, что при n=1 из этой формулы получается плотность распределения Коши:
pT1(t)= 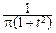 ,
,
т. е. случайную величину, распределенную по закону Коши, можно считать отношением двух независимых случайных величин, X= 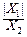 , где Xi~N(0, 1), i=1, 2.
, где Xi~N(0, 1), i=1, 2.
Замечание. Часто случайную величину Tnопределяют с дополнительным множителем: Tn= 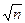 ×
× 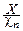 . В этом случае плотность вероятности имеет вид:
. В этом случае плотность вероятности имеет вид:
pTn(t)= 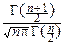 ×(1+
×(1+ 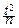 )
) 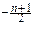 .
.
Дополнительные множители появляются и в выражении для функции распределения.
Числовые характеристики случайных величин:
математическое ожидание, дисперсия,
коэффициент корреляции
Наиболее полная информация о случайной величине содержится в законе её распределения. Более бедную, но зато и более конкретную информацию о ней дают её числовые характеристики. Простейшей из них является математическое ожидание, которое интерпретируется как среднее значение случайной величины. Если посмотреть на закон распределения как на распределение единичной вероятностной массы между значениями случайной величины, то в качестве среднего значения можно взять координаты центра тяжести этой массы. По известным из анализа и механики формулам получаем формулы для вычисления абсциссы центра тяжести:
 xp(x)dx – в непрерывном случае,
xp(x)dx – в непрерывном случае,
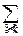 xkpk– в дискретном случае.
xkpk– в дискретном случае.
Для того, чтобы дать определение, пригодное и для общего случая, необходимо обобщить понятие риманова интеграла.
Сделаем поэтому небольшое математическое отступление.
––²––
Интеграл Стилтьеса
Интеграл Стилтьеса определяется для двух функций: одна из них j(x) – называется интегрируемой, другая F(x) – интегрирующей. Разобьём всю ось на интервалы Dtk: [tk, tk+1), относя для определённости к интервалу левый конец и исключая правый. В каждом интервале выберем произвольно точку xkи составим интегральную сумму
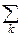 j(xk)[F(tk+1)-F(tk)].
j(xk)[F(tk+1)-F(tk)].
Перейдём к пределу, устремив наибольший из интервалов к нулю. Если предел существует и не зависит ни от способа разбиения оси на интервалы, ни от способа выбора точек xkна них, то он называется интегралом Стилтьеса от функции j(x) по функции F(x) и обозначается:  j(x)dF(x).
j(x)dF(x).
Легко убедиться в том, что обычные свойства интеграла сохраняются: постоянный множитель можно выносить за знак интеграла, интеграл от суммы равен сумме интегралов.
Интеграл Римана является частным случаем интеграла Стилтьеса для F(x)=x.
Рассмотрим два частных случая:
a. F(x) – ступенчатая функция, имеющая в точках xiскачки величины piи постоянная между этими точками. Приращения F(tk+1)-F(tk) на тех интервалах Dtk, которые не содержат точек разрыва функции F(x), равны нулю; если же точка xiявляется единственной точкой разрыва F(x), содержащейся в интервале Dtk, то разность F(tk+1)-F(tk) равна pi. Считая, что все точки разрыва изолированные, при переходе к пределу получим:  j(x)dF(x)=
j(x)dF(x)= 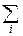 j(xi)pi.
j(xi)pi.
b. F(x) – дифференцируемая функция: существует производная F¢(x)=p(x). В интегральной сумме для интеграла Стилтьеса 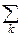 j(xk)[F(tk+1)-F(tk)] каждую из разностей [F(tk+1)-F(tk)] заменим по формуле Лагранжа: на каждом промежутке Dtkнайдётся такая точка hk, в которой F(tk+1)-F(tk)=F¢(hk)=
j(xk)[F(tk+1)-F(tk)] каждую из разностей [F(tk+1)-F(tk)] заменим по формуле Лагранжа: на каждом промежутке Dtkнайдётся такая точка hk, в которой F(tk+1)-F(tk)=F¢(hk)=
=p(hk)Dtk; пользуясь произволом в выборе точек xkиз промежутка Dtk, возьмём в каждом слагаемом интегральной суммы xk=hkи тогда сумма примет вид:
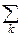 j(hk)p(hk)Dtk,
j(hk)p(hk)Dtk,
а это – ни что иное, как риманова интегральная сумма для функции j(x)p(x). Поэтому:
 j(x)dF(x)=
j(x)dF(x)=  j(x)p(x)dx.
j(x)p(x)dx.
В теории вероятностей интеграл Стилтьеса оказался удобным средством объединения случаев непрерывного и дискретного распределений в общем случае.
––²––
Вернёмся к изучению числовых характеристик случайных величин.
1°. Выше мы ввели понятие математического ожидания для дискретной и непрерывной случайных величин.
Пусть теперь X – случайная величина с функцией распределения F(x). Возьмём произвольную функцию j(x).
Назовём математическим ожиданием функции j от случайной величины X число Mj(X), определяемое равенством:
Mj(X)=  j(x)dF(x).
j(x)dF(x).
В частности, для непрерывной случайной величины с плотностью вероятности p(x) получаем:
Mj(X)=  j(x)p(x)dx,
j(x)p(x)dx,
а для дискретной случайной величины с распределением pk=P{X=xk}:
Mj(X)= 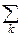 j(xk)pk.
j(xk)pk.
В случае, когда j(x)=x, последние три формулы принимают вид:
MX=  xdF(x) – в общем случае,
xdF(x) – в общем случае,
MX=  xp(x)dx – в непрерывном случае,
xp(x)dx – в непрерывном случае,
MX= 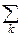 xkpk– в дискретном случае.
xkpk– в дискретном случае.
Формулы для непрерывного и дискретного случаев совпали с формулами для абсциссы центра тяжести распределения вероятностной массы, и тем самым оправдывается истолкование математического ожидания случайной величины X как среднего значения.
Для корректности определения математического ожидания следует обсудить вопрос о его существовании и единственности.
Вопрос о единственности Mj(X) возникает потому, что j(X) сама является случайной величиной со своей функцией распределения Fj(x) и в соответствии с нашим определением её математическое ожидание равно  xdFj(x).
xdFj(x).
Для однозначности определения необходимо выполнение равенства
 j(x)p(x)dx=
j(x)p(x)dx=  xdFj(x)
xdFj(x)
и такое равенство действительно можно доказать: оно даёт правило замены переменных в интеграле Стилтьеса. Мы здесь вынуждены принять его без доказательства.
Вопрос о существовании математического ожидания: ясно, что в непрерывном и дискретном случае любая ограниченная случайная величина имеет математическое ожидание. Если же X может принимать сколь угодно большие значения, то в дискретном случае сумма, определяющая MX, становится бесконечным рядом, а в непрерывном – интеграл становится несобственным, причём оба могут расходиться. Очевидно, в непрерывном случае достаточным условием существования среднего значения у случайной величины является
p(x)=O( 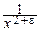 ) при x®±¥ (e>0),
) при x®±¥ (e>0),
а в дискретном случае:
xkpk=O( 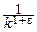 ) при k®¥ (e>0).
) при k®¥ (e>0).
Однако оба эти условия не являются необходимыми.
Легко также придумать примеры случайных величин, не имеющих среднего. Для непрерывного случая таким примером может служить распределение Коши. В дискретном подобный пример придумать ещё проще, если учесть, что вероятность pkможно приписать сколь угодно большим числам xk.
Если дана двумерная случайная величина (X, Y), то математическое ожидание функции j(X, Y) определяется равенствами
Mj(X, Y)= 
 j(x, y)p(x, y)dxdy – в непрерывном случае
j(x, y)p(x, y)dxdy – в непрерывном случае
(интеграл берётся по всей плоскости),
Mj(X, Y)= 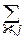 j(xi, yj)pij– в дискретном случае
j(xi, yj)pij– в дискретном случае
(сумма берётся по всем возможным значениям
двумерной случайной величины).
2°. Второй по важности числовой характеристикой случайной величины X служит её дисперсия DX. Дисперсией называется
DX=M[(X-MX)2]=  (x-MX)2dF(x),
(x-MX)2dF(x),
т. е. среднее значение квадрата отклонения случайной величины от её среднего. Эта формула в непрерывном случае переходит в
DX=  (x-MX)2p(x)dx,
(x-MX)2p(x)dx,
а в дискретном в:
DX= 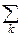 (xk-MX)2pk.
(xk-MX)2pk.
Если среднее есть не у всех случайных величин, то дисперсия и подавно. В дальнейшем все теоремы о MX и DX без особых оговорок формулируются лишь для тех X, которые их имеют.
Размерность дисперсии равна квадрату размерности случайной величины X. Поэтому иногда удобно вместо DX рассматривать величину sX= 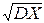 , называемую средним квадратичным отклонением случайной величины X или просто стандартом.
, называемую средним квадратичным отклонением случайной величины X или просто стандартом.
Дисперсия и стандарт мыслятся как меры разброса значений случайной величины вокруг её среднего.
3°. Докажем несколько простых утверждений:
Математическое ожидание постоянной C равно C: MC=C.
Постоянный множитель можно выносить за знак математического ожидания:
M(CX)=CMX.
Дисперсия постоянной равна нулю: DC=0.
Постоянный множитель выносится за знак дисперсии в квадрате:
D(CX)=C2DX.
Постоянную C можно рассматривать как частный случай дискретной случайной величины, принимающей единственное значение C с вероятностью, равной 1. Поэтому MC=C×1=C.
Свойство M(CX)=CMX следует из определения математического ожидания как предела интегральных сумм: постоянный множитель можно выносить за знак суммы и знак интеграла.
О дисперсии:
DC=M[(C-MC)2]=M[(C-C)2]=M0=0;
D(CX)=M[(CX-M(CX))2]=M[(CX-CM(X))2]=
=M[C2(C-MC)2]=C2×M[(X-MX)2]=C2DX.
4°. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:
M(X+Y)=MX+MY.
Докажем эту теорему отдельно для непрерывного и дискретного случая.
a. Непрерывный случай. Пусть p(x, y) – двумерная плотность вероятности.
Согласно определению математического ожидания функции от двумерной случайной величины:
M(X+Y)= 
 (x+y)p(x, y)dxdy.
(x+y)p(x, y)dxdy.
Представляя двойной интеграл как сумму двух повторных и выбирая соответствующий порядок интегрирования в слагаемых, имеем:
M(X+Y)=  xdx
xdx  p(x, y)dy+
p(x, y)dy+  ydy
ydy  p(x, y)dx=
p(x, y)dx=
=  xpX(x)dx+
xpX(x)dx+  ypY(y)dy=MX+MY.
ypY(y)dy=MX+MY.
b. Дискретный случай.
M(X+Y)= 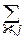 (xi+yj)pij.
(xi+yj)pij.
Представляем двойную сумму как две повторные:
M(X+Y)= 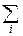 xi
xi 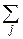 pij+
pij+ 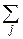 yi
yi 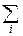 pij=
pij= 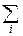 xipi+
xipi+ 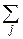 yjpj=MX+MY.
yjpj=MX+MY.
Аналогично эту теорему можно доказать для смешанного случая. Общая же формулировка потребовала бы введения двумерного интеграла Стилтьеса.
5°. Предыдущая теорема естественно обобщается на сумму n слагаемых:
M 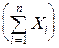 =
= 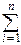 MXi.
MXi.
Как частный случай применения этой формулы отметим следующую задачу: имеются события A1, A2, ¼ , An, их вероятности соответственно равны p1, p2, ¼ , pn. Спрашивается, чему равно ожидаемое число событий A1, A2, ¼ , An, которые произойдут в опыте? Определим вспомогательные случайные величины Xiравенствами:
|
0, если событие Aiне произошло.
Всего в опыте происходит 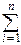 Xi событий, а ожидаемое число равно
Xi событий, а ожидаемое число равно
M 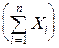 =
= 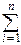 MXi=
MXi= 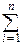 pi.
pi.
6°. Ещё одна формула для дисперсии: DX=M(X2)-M2(X).
Действительно, в силу теорем 3° и 4° имеем:
DX=M[(X-MX)2]=M(X2)-MX×MX+M[M(X)2]=
=M(X2)-2.M2(X)+M2(X)=M(X2)-M2(X).
В частности, если MX=0, то DX=M(X2).
7°. Нормированной случайной величиной X*назовём:
X*= 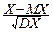 .
.
Это – безразмерная случайная величина, причём:
a) MX*=0, b) M(X*2)=1, c) DX*=1.
Действительно, по теореме 3° и 4°:
MX*=M( 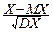 )=
)= 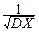 (MX-MX)=0,
(MX-MX)=0,
M(X*2)=M[ 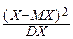 ]=
]= 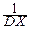 M[(X-MX)2]=
M[(X-MX)2]= 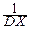 DX=1,
DX=1,
DX*=M(X*2)-(MX*)2=1-0=1.
8°. Если DX=0, то почти наверное X=const. Действительно,
DX=  (x-MX)2dF(x).
(x-MX)2dF(x).
Интегрируемая функция (x-MX)2 неотрицательна, причём обращается в ноль, только в точке x=MX. Интегрирующая функция F(x) монотонно неубывающая, причём её наименьшее значение ³0, а наибольшее £1. Очевидно, равенство DX=0 возможно лишь в том случае, когда весь рост функции F(x) сосредоточен в точке MX, а это и означает, что X=const почти наверное.
9°. Пусть дана двумерная случайная величина (X, Y). Назовем коэффициентом корреляции двумерной случайной величины число
r=r(X, Y)=M(X*, Y*)= 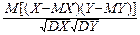 .
.
Числитель здесь называется ковариацией случайных величин X и Y:
cov(X, Y)=M[(X-MX)(Y-MY)]=M(XY)-MX×MY.
Из определения коэффициента корреляции следует, что
cov(X, Y)=r× 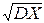 ×
× 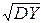 .
.
Очевидно, коэффициент корреляции не меняется при линейном преобразовании случайных величин; в частности, r(X, Y)=r(X*, Y*).
Коэффициент корреляции – числовая характеристика пары случайных величин, определённых на одном и том же вероятностном пространстве, –заслужил репутацию меры линейной связи величин X и Y.
Основанием к этому служат последующие теоремы о коэффициенте корреляции.
10°. M(XY)=MX×MY+cov(X, Y) или M(XY)=MX×MY+r× 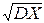 ×
× 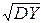 .
.
Действительно:
M(XY)=M{[(X-MX)+MX]×[(Y-MY)+MY]}=
=M[(X-MX)×(Y-MY)