Основные модели управления запасами.

При описании движения запаса используют две оси перемен­ных: объем запаса и время.

Изменение объема запаса во времени — основная проблема обеспечения потребности в запасе данного места хранения. Не­обходимо содержать запас в таком объеме, чтобы, невзирая на особенности реализации пополнения и потребления запаса, он всегда был достаточен для обслуживания потребления на задан­ном уровне.

Ранее отмечалось, что запас формируется под воз­действием входящего и выходящего материальных потоков. Не имея возможности напрямую влиять на характерис­тики потребности в запасе, специалисты по управлению запасами используют возможности влиять на характеристики поставки. При этом главными вопросами являются объем заказа и момент, когда следует заказать товарно-материальные ценности для вос­полнения запаса.

Оба вопроса взаимосвязаны. Исходя из принятого размера по­полнения запаса, необходимого для удовлетворения заданной или прогнозируемой (планируемой) потребности, можно определить моменты подачи заказов. Значение экономически целесообразно­го размера заказа — ключевой параметр оптимизации уровня за­паса в организации. Именно от его величины зависят дальнейшее поведение запаса и управление им.

Для манипуляции запасом у специа­листов по управлению запасами имеется только два инструмента: 1) размер заказа и 2) интервал времени между заказами. Исходя из этого можно сказать, что имеется только две возможности построе­ния модели управления запасами. Первая состоит в фиксировании размера заказа. Тем самым специалисты получают однозначный ответ на вопрос об объеме восполнения запаса. Вторая возмож­ность — зафиксировать интервал времени между заказами, тем самым однозначно ответив на вопрос о моменте, когда следует вы­дать заказ на восполнение запаса.

Таким образом, теоретически имеется две модели управления запасами:

1) модель управления запасами с фиксированным размером за­каза (или двухбункерная система (two-bin system));

2) модель управления запасами с фиксированным интервалом времени между заказами.

Эти модели являются основными в управлении запасами. Все огромное разнообразие алгоритмов управления запасами основы­вается на методике фиксированного размера заказа или методике фиксированного интервала времени между заказами.

Основным допущением классических моделей управления запасами с фиксированным раз­мером заказа и фиксированным интервалом времени между зака­зами является постоянство (или усреднение) объема потребности в запасе в единицу времени. Объ­ем потребности в запасе, как правило, меняется с течением време­ни. Для учета вероятности изменения объема потребности исполь­зуются варианты моделей с фиксированным размером заказа и фиксированным интервалом времени между заказами на основе математических моделей. Следует учитывать, что практика управления запасами ориентирована на оперативные решения и гибкое использование методов, что зачас­тую требует упрощения математического аппарата.

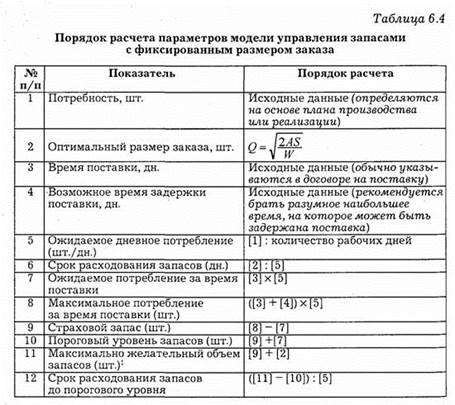
Основной параметр модели с фиксированным размером за­каза — размер заказа, который вычис­ляется описанным в предыдущей задаче способом. Таким обра­зом, главный критерий оптимизации в такой модели — мини­мизация совокупных затрат на хранение запасов и размещение заказа (если мы заказываем продукцию редко, но большими партиями, возникают затраты, связанные с хранением и порчей продукции, если заказываем часто — возникают затраты, свя­занные с транспортировкой маленьких партий, отсутствием оп­товых скидок и т. д.).

Методика расчета основных параметров модели приведена в табл. 4.1.

Таблица 4.1

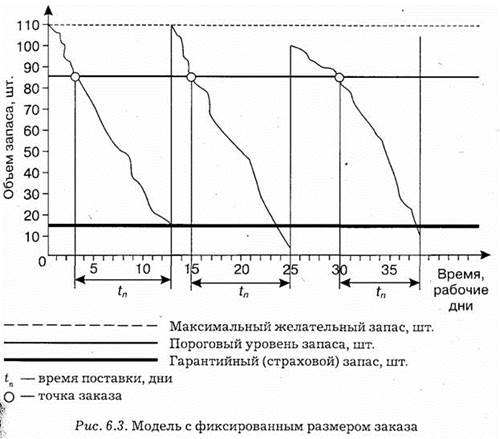
Схематично модель управления запасами с фиксированным размером заказа изображена на рис. 4.1.

Рисунок 4.1. Модель с фиксированным размером заказа

В работе системы с фиксированным интервалом времени между заказами оптимальный размер заказа непосредственно не исполь­зуется. Однако эффективный интервал времени между заказами, являющийся исходным параметром данной модели, предлагается исходя из оптимального размера заказа.

Отношение величины потребности к оптимальному размеру за­каза равно количеству заказов в заданный период, а число рабочих дней в заданном периоде, отнесенное к количеству заказов, равно интервалу между заказами, соответствующему оптимальному ре­жиму работы системы.

Следовательно, интервал времени между заказами можно рас­считать по следующей формуле:

I = NxQ/S, (4.1)

где I — интервал времени между заказами, дн.;

N — число рабочих дней в периоде, дн.;

Q — оптимальный размер заказа, шт.;

S— потребность, шт.

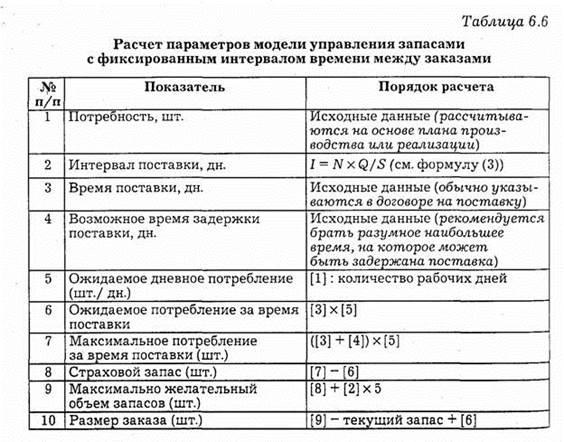
Методика расчета основных параметров модели приведена в табл. 4.2.

Таблица 4.2

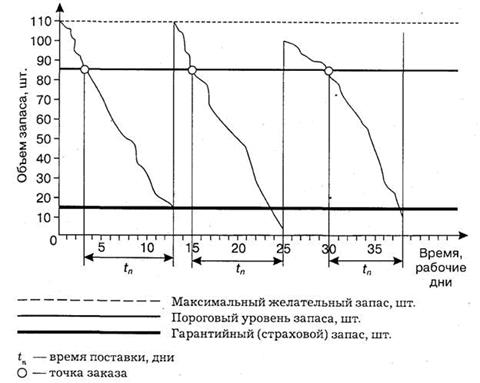
Схематично модель управления запасами с фиксированным интервалом времени между заказами изображена на рис. 4.2.

	Рисунок 4.2. Модель с фиксированным интервалом времени между заказами

В целом можно отметить, что модель с фиксированным размером заказа по сравнению с моделью с фиксированным интервалом вре­мени между заказами чаще приводит к экономии затрат на содер­жание запаса на складе за счет сокращения площадей под запаса­ми. В то же время модель с фиксированным интервалом времени между заказами требует лишь периодического контроля количества запасов. Это упрощает процедуру использования модели и сокра­щает операционные затраты.