Устранение статической ошибки

Следует заметить, что при модальном синтезе ставится задача обеспечения заданной формы переходного процесса, но при этом не обеспечивается автоматически желаемый уровень выходного сигнала. Эта проблема решается путем введения масштабирующего коэффициента для входного воздействия.

Рассмотрим разомкнутую систему (рис. 1.3). При подаче на вход единичного скачка

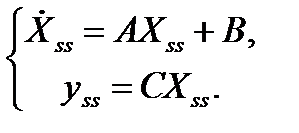
где X_ss – установившееся состояние; y_ss – установившееся значение выхода.

По окончании переходного процесса выполняется условие:

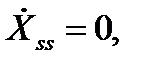
Таким образом

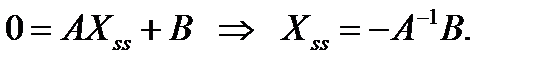
Следовательно, установившаяся ошибка равна

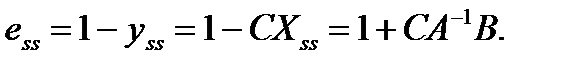
Аналогично для системы, замкнутой обратной связью по состоянию при единичном скачке:

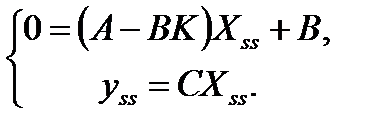
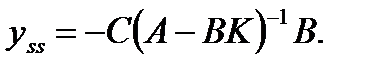
Для устранения статической ошибки надо умножить входной сигнал на масштабирующий коэффициент:

Пример 2.9. Рассмотрим систему, заданную матрицами (пример 2.6)

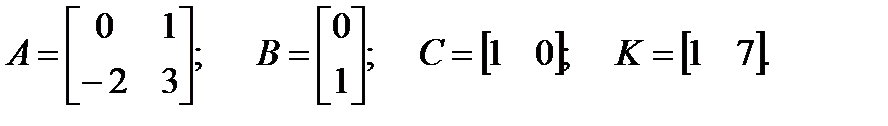
Для этой системы

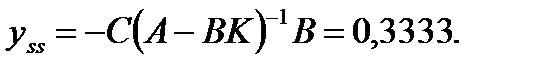
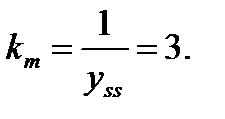
В общем случае для устранения статической ошибки в структуру регулятора может быть введена внутренняя модель эталонного сигнала. Это позволяет асимптотически отслеживать изменение входного сигнала с нулевой установившейся ошибкой.

В качестве эталонного входного сигнала могут выступать ступенчатый, линейный или синусоидальный сигнал.

Рассмотрим объект типа SISO (Single Input Single Output)

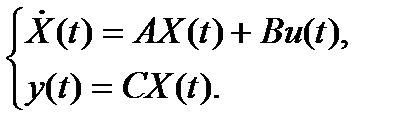
Эталонный входной сигнал генерируется линейной системой, описываемой такого же вида системой уравнений при нулевых начальных условиях:

Эта система соответствует полиному

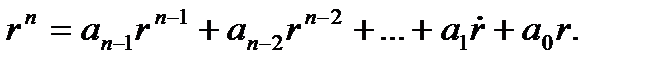
Рассмотрим ступенчатый входной сигнал. Для этого сигнала dr/dt=0, и ошибка воспроизведения

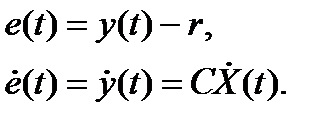
Также можно записать

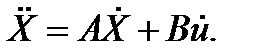
Введем вспомогательные переменные

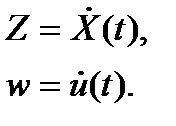
Тогда можно записать

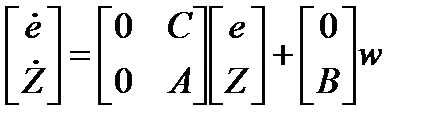
Если эта система является управляемой, то можно сформулировать такой сигнал обратной связи по состоянию

чтобы ошибка асимптотически стремилась к нулю.

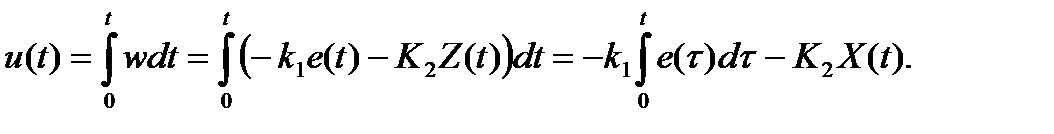
Структура системы управления будет иметь вид, показанный на рис. 2.3.

r(t)

y(t)

K2

Объект

ò

e(t)

k1

u(t)

X(t)

регулятор

Рис. 2.3. Использование внутренней модели для единичного скачка

Интегратор здесь является внутренней моделью ступенчатого входного сигнала.

Пример 2.10. Пусть объект управления описывается уравнениями

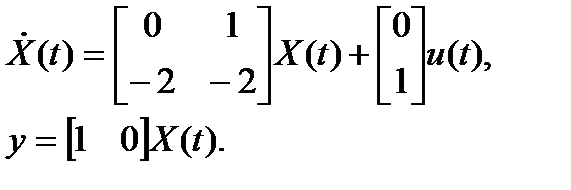
Требуется обеспечить воспроизведение системой ступенчатого входного сигнала с нулевой установившейся ошибкой.

Введем новые переменные, расширяющие вектор состояния системы:

Эта система управляема, поэтому можно выбрать желаемое положение корней замкнутой системы, и гарантировать, что при любой начальной ошибке e → 0 при t →¥.

Рассмотрим далее линейный входной сигнал

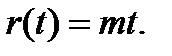
Для этого сигнала d²r/dt² = 0, и ошибка воспроизведения

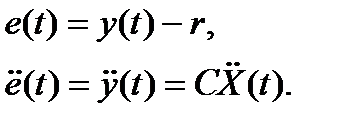
Введем вспомогательные переменные

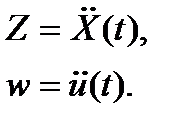
Составляется система

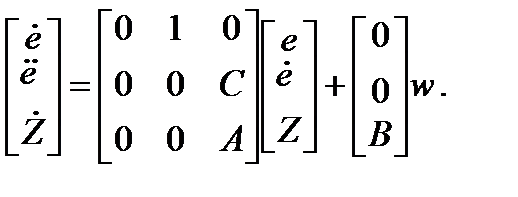
Если эта система управляема, то можно найти вектор коэффициентов обратной связи, при которых система будет асимптотически устойчива.

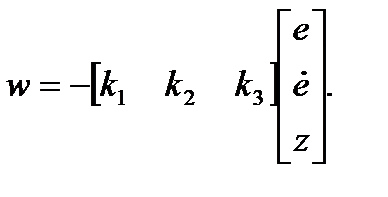
Так как w = d²u/dt²,

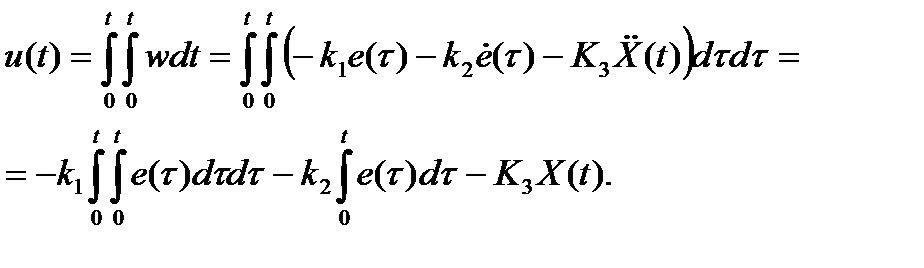
Этому выражению соответствует структура, показанная на рис. 2.3.

r(t)

y(t)

K3

Объект

ò

e(t)

k1

u(t)

X(t)

k2

ò

Рис. 2.4. Использование внутренней модели для линейного входного сигнала

Таким образом, здесь два интегратора представляют собой внутреннюю модель эталонного линейного входного сигнала.

Метод внутренней модели может быть использован и для других эталонных сигналов, процедура синтеза остается такой же.