Введение: Методические указания для работы с материалом кейса

Виды эконометрических моделей

Различают линейные и нелинейные эконометрические модели.

Линейная эконометрическая модельописывается уравнением:

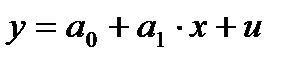(1.1)

где y – объясняемая (эндогенная) переменная,

a₀, a₁ – параметры модели,

x – объясняющая (экзогенная) переменная,

u – случайная переменная.

Нелинейные парные эконометрические моделиделятся на два класса:

1) модели, нелинейные по объясняющим переменным, но линейные по параметрам, например:

• равносторонняя гипербола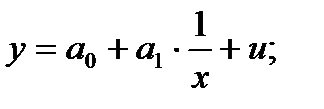

2) модели, нелинейные по параметрам, например:

• степенная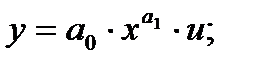

• показательная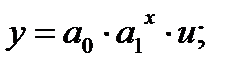

• экспоненциальная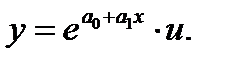

Для построения парной линейной регрессии вычисляют следующие вспомогательные величины (для выборки из 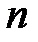наблюдений).

См. дополнительно литературу: [1, с. 31 - 35, c. 178 - 186]; [2, с. 60 - 63, с. 331 - 332]; [3, с. 49-71]; [5, с. 13 - 19, с. 52 - 60]; [7, с. 41 - 48, с. 62 - 80]; [8]; [9].

Оценивание параметров парной линейной эконометрической модели

Для исходной парной линейной эконометрической модели, представленной в виде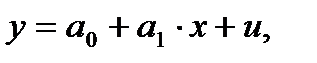необходимо построить парную линейную регрессию вида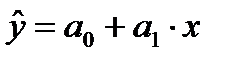

Построение линейной регрессии 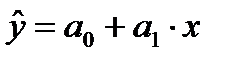сводится к оценке ее параметров 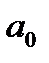и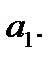

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 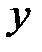от оценочного 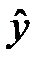минимальна, т.е.

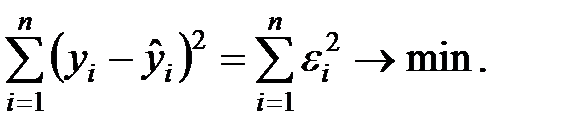(1.8)

Для линейной регрессии параметры 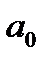и 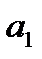находятся из системы нормальных уравнений:

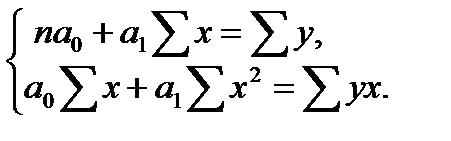(1.9)

Решая систему, находим оценку коэффициента парной линейной регрессии:

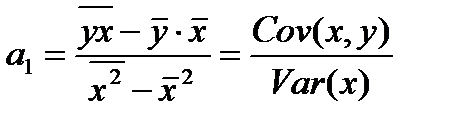(1.10)

и постоянный коэффициент

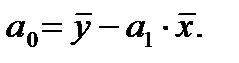(1.11)

Коэффициент 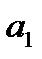при объясняющей переменной 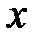показывает, насколько изменится в среднем величина 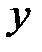при изменении значения 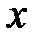на единицу.

См. дополнительно литературу: [1, с. 35 - 44]; [2, с. 148 - 153]; [3, с. 49 - 71]; [5, с. 50 - 56]; [7, с. 41 - 48]; [8]; [9].

Теорема Гауса-Маркова и проверка ее гипотез

Если имеется выборка значений переменных y и x

(y₁,x₁), (y₂, x₂), …. ,(y_n,x_n)

линейной модели парной регрессии 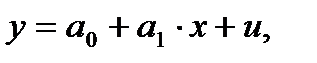то в рамках этой модели величины (y₁,x₁), (y₂, x₂), …. ,(y_n,x_n) связаны системой уравнений наблюдения объекта в виде линейных алгебраических уравнений:

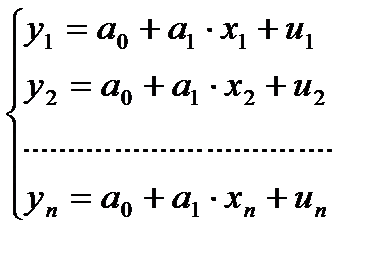(1.12)

Данная система называется схемой Гауса-Маркова. В матричном виде она имеет вид:

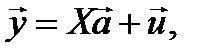(1.13)

где

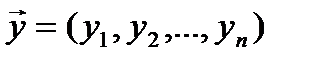- вектор наблюдений объясняющей переменной y,

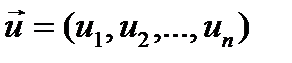- ненаблюдаемый вектор случайных возмущений (остатков),

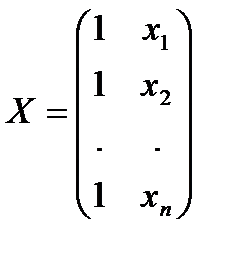- расширенная матрица наблюдаемых значений объясняющей переменной x,

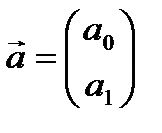- вектор столбец неизвестных параметров парной линейной эконометрической модели, которые подлежат оцениванию по имеющейся выборке.

Теорема Гауса-Маркова

Если имеется матрица X уравнений наблюдений размером n x (k+1), где n > k+1, имеющая линейно-независимые столбцы, а случайные возмущения u_i (i == 1,n), удовлетворяют следующим условиям:

E(u₁) = E(u₂) = … = E(u_n) = 0, (1.14)

Var(u₁) = Var(u₂)= …= Var(u_n) = σ_u², (1.15)

Cov(u_i,u_j) = 0 для всех i ≠ j, (1.16)

Cov(x_i,u_j) = 0 для всех i и j, (1.17)

то тогда наилучшей линейной процедурой нахождения параметров эконометрической модели является метод наименьших квадратов (МНК), позволяющий найти эффективные и несмещенные оценки параметров модели.

При этом предполагается, что случайные остатки в уравнениях наблюдений распределены по нормальному закону.

Таким образом, для того, чтобы воспользоваться МНК для оценки параметров парной эконометрической модели, необходимо соблюдение всех четырех условий теоремы Гауса-Маркова.

Если соблюдается условие (1.15), то говорят, что случайные остатки в модели гомоскедастичные, в противном случае – гетероскедастичные.

См. дополнительно литературу: [1, с. 45 - 47]; [2, с. 153 - 162]; [3, с. 72 - 117]; [5, с. 60 - 64]; [7, с. 155 - 169]; [8]; [9].

Тест Голдфелда-Квандта

Тест Голдфелда-Квандта предназначен для проверки условия (1.15) теоремы Гауса-Маркова о гомоскедастичности случайного остатка в модели, т.е. проверяется статистическая гипотеза о равенстве дисперсий случайных остатков в наблюдаемых уравнениях

Н₀: Var(u₁) = Var(u₂)= …= Var(u_n) = σ_u²

Реализация теста осуществляется по следующему алгоритму:

Шаг 1. Уравнения наблюдений 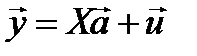упорядочивают по возрастанию объясняющей переменной x.

Шаг 2. Полученный отсортированный массив разбивают на две равные части (n₁ = n₂ = n/2). Если массив большой или количество значений в массиве нечетное (для небольших массивов), то его разбивают на 3 части (n₁ = n₃ ≈ 0,3n). При этом число элементов в первой части и число элементов в третьей части должны быть одинаковыми.

Шаг 3. Для первой части отсортированного массива рассчитывается величина ESS₁[1]:

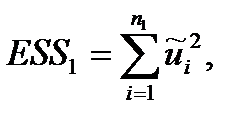(1.18)

где 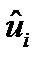- оценка случайного возмущения (остатков) u_i

Шаг 4. Аналогично рассчитывается величина ESS₂ для другой части отсортированного массива:

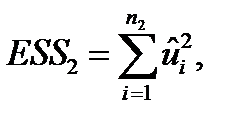
Шаг 5. Вычисляется статистика Голдфелда-Квандта (GQ):

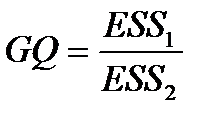и обратная ей 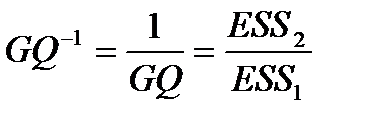(1.19)

Шаг 6. Задается уровень значимости α и при количествах степеней свободы обоих частей массива v₁ = v₂ = n₁-(k+1) определяется F_крит = F_1-α распределения Фишера по таблице 1 (см. Приложение 1), либо, если для расчетов применяется табличный процессор Excel, то F_крит можно рассчитать, используя функцию FРАСПОБР(1- α; v₁, v₂).

Шаг 7. Гипотеза Н₀ принимается, если справедливы следующие два неравенства

GQ ≤ F_крит ,

GQ^-1 ≤ F_крит , (1.20)

т.е. случайный остаток в парной эконометрической модели в этом случае полагается гомоскедастичным. В противном случае гипотеза Н₀ отклоняется и делается вывод, что случайный остаток в парной эконометрической модели является гетероскедастичным.

См. дополнительно литературу:[1, с. 32 - 49 ], [2, с. 186 - 189]; [5, с. 157 - 163]; [7, с. 41 - 48, с. 62 - 80]; [8]; [9].

Тест Дарбина – Уотсона

Тест Дарбина – Уотсона предназначен для проверки условия (1.3) теоремы Гауса - Маркова, т.е. проверки следующей гипотезы Н₀:

Н₀: Cov(u_i,u_j) = 0 для всех i ≠ j

Реализация теста осуществляется по следующему алгоритму:

Шаг 1. По уравнениям наблюдений 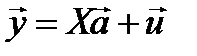вычисляются оценки параметров модели и оценки случайных остатков .

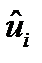Шаг 2. Вычисляется значение статистики Дарбина – Уотсона (DW) по формуле:

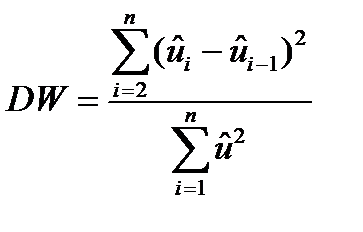(1.21)

Областью изменения статистики DW является интервал (0,4).

Шаг 3. Из таблицы 2 (см. Приложение 1) по количеству наблюдений (n) и количеству (k) объясняющих переменных выбираются значения величин d_L и d_U.

Шаг 4. Проводится проверка, в какой из пяти подмножеств (0, d_L), (d_L, d_U,), (d_U, 4- d_U), (4- d_U, 4- d_L), (4- d_L, 4) интервала (0,4)попадает рассчитанное значение статистики DW (см. рис. 1.1), и делается вывод:

	cov>0	?	cov=0	?	cov<0
	dL	dU		4-dU	4-dL

Рисунок 1.1.

а) если значение статистики DW попадает в третий интервал (d_U, 4- d_U), то подтверждается гипотеза:

Н₀: Cov(u_i,u_j) = 0 для всех i ≠ j,

б) если значение статистики DW попадает в первый интервал (0, d_L), то гипотеза Н₀ не подтверждается, а принимается альтернативная гипотеза:

Н₁: Cov(u_i,u_j) > 0,

в) если значение статистики DW попадает в пятый интервал (4- d_L, 4), то гипотеза Н₀ не подтверждается, а принимается альтернативная гипотеза:

Н₁: Cov(u_i,u_j) < 0,

г) если значение статистики DW попадает во второй (d_L, d_U,) или четвертый (4- d_U, 4- d_L) интервал, то отклонить или принять гипотезу Н₀ не удается с использованием данного теста.

Тест Дарбина-Уотсона предполагает, что соблюдаются другие условия теоремы Гауса-Маркова.

См. дополнительно литературу:[1, с .32-49], [2, с. 60 - 63, с. 331 - 332]; [3, с. 72-117]; [5, с. 170 - 178]; [7, с. 272 - 278]; [8]; [9].

F - тест

Оценка значимости уравнения регрессии проводится с помощью 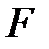-критерия Фишера, который заключается в проверке гипотезы о статистичес­кой незначимости уравнения регрессии. Для этого выполняется сравнение фактического 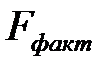и критического (табличного) 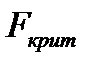значений 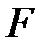- крите­рия Фишера.

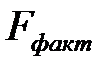определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы, т.е.

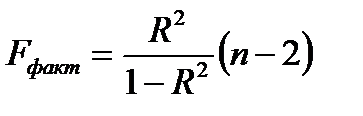или 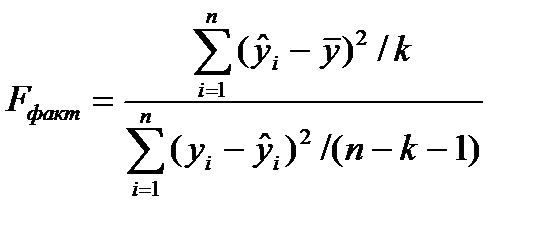(1.25)

где n – численность выборки,

k – количество оцениваемых параметров при х (количество регрессоров).

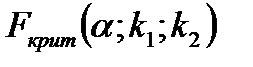– максимально возможное значение критерия под влиянием случайных факторов при степенях свободы 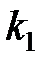=1, 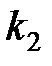= 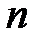-2 и уровне значимости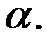 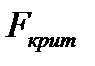находится из таблицы 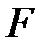-критерия Фишера (Таблица 1 Приложение 1), либо, если для расчетов применяется табличный процессор Excel, то его можно рассчитать, используя функцию FРАСПОБР(α;ν₁;ν₂).

Уровень значимости 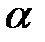– это вероятность отвергнуть правильную гипотезу при условии, что она верна.

Если 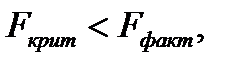то гипотеза об отсутствии связи изучаемого показателя с фактором отклоняется и делается вывод о существенности этой связи с уровнем значимости 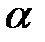(т.е. уравнение регрессии значимо).

Если 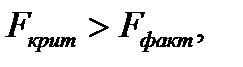то гипотеза принимается и признается статистическая незначимость и ненадежность уравнения регрессии.

T – тест

Для линейной регрессии значимость оцененных коэффициентов регрессии определяется с помощью 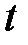-критерия Стьюдента, согласно которому выдвигается гипотеза о случайной природе показателей, т.е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия 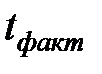для каждого из оцениваемых коэффициентов регрессии, т.е.

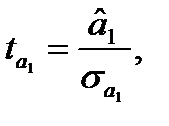(1.26)

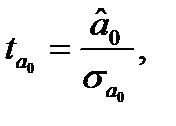(1.27)

где 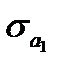и 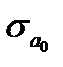– стандартные ошибкипараметров линейной регрессии определяются по формулам:

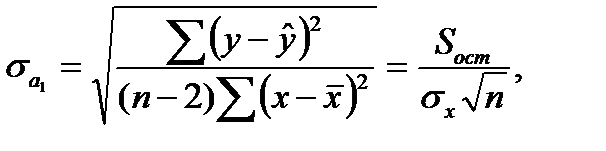(1.28)

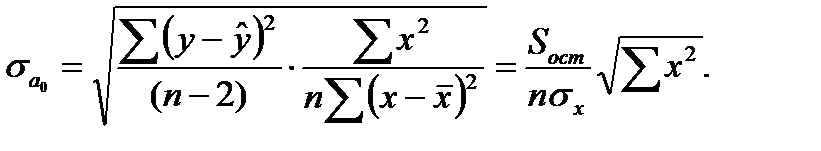(1.29)

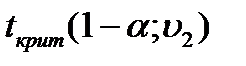– максимально возможное значение критерия Стьюдента под влиянием случайных факторов при данной степени свободы 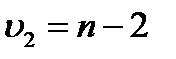и уровне значимости 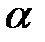находится из таблицы критерия Стьюдента (таблица 2 приложение 1), либо, если для расчетов применяется табличный процессор Excel, то его можно рассчитать, используя функцию CТЬЮДРАСПОБР(1-α;υ₂).

Если 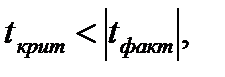то гипотеза о несущественности коэффициента регрессии отклоняется с уровнем значимости 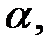т.е. коэффициент ( 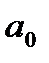или 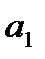)не случайно отличается от нуля и сформировался под влиянием систематически действующего фактора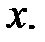

Если 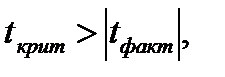то гипотеза не отклоняется и признается случайная природа формирования параметра.

При проверке статистической значимости параметров модели можно использовать следующее приближенное правило[2]:

1) если |t_фак| <1, то данный коэффициент не может быть признан значимым (доверительная вероятность меньше 0,7);

2) если 1< |t_фак| <2, то данный коэффициент может быть признан значимым c доверительной вероятностью в диапазоне между 0,7 – 0,95;

3) 2< |t_фак| <3, то данный коэффициент может быть признан значимым c доверительной вероятностью в диапазоне между 0,95 – 0,99;

4) если |t_фак| >3, то значимость данного коэффициента очевидна (доверительная вероятность находится в диапазоне между 0,99 и выше).

При этом, чем больше объем выборки, тем надежнее вывод о значимости коэффициента.

См. дополнительно литературу: [1, с. 66 – 72], [2, с 302 -315], [3, c. 72 - 117], [5, с. 50-80], [7, с. 34 - 48], [8]; [9] [ ]

Значимость линейного коэффициента корреляции также проверяется с помощью 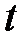-критерия Стьюдента, т.е.

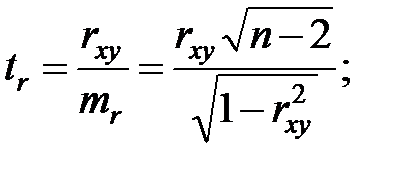
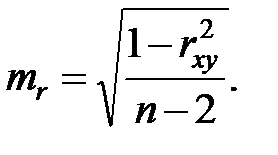(1.30)

Гипотеза о несущественности коэффициента корреляции отклоняется с уровнем значимост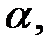и если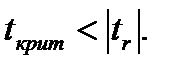

Замечание. Для парной линейной регрессии проверка гипотезы о значимости коэффициента 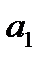и коэффициента корреляции 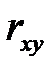равносильна проверке гипотезы о существенности уравнения регрессии в целом, т.е.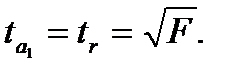

Для каждого полученного параметра парной линейной регрессии сначала рассчитывают предельную ошибку:

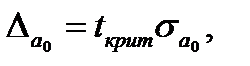
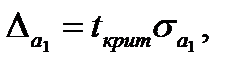(1.31)

а затем рассчитываются доверительные интервалы:

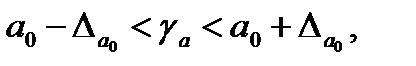(1.32)

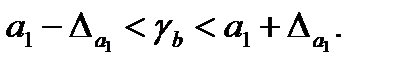
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается равным нулю, так как он одновременно не может принимать и положительное, и отрицательное значения.

См. дополнительно литературу: [1, с. 31 - 62]; [2, с. 302 -316]; [3, c. 72 -117]; [5, с. 60 - 64]; [7, с. 48 - 57]; [8]; [9].

Пример построения и исследования парной линейной эконометрической модели

Задача. Сотрудник муниципального образования должен подготовить обоснованные предложения к проекту плана развития района на 2014 и 2015 гг. по графе «Потребительские расходы в расчете на душу населения» в зависимости от средней заработной платы и выплат социального характера. У сотрудника имеются статистические данные по этим показателям с 1990 г. по 2013 г. (см. табл. 2.1). При этом планом предусмотрено, что в 2014 г рост заработной платы и выплаты социального характера увеличатся на 8% по сравнению со средним значением за последние 5 лет, а в 2015 г – увеличатся на 12%.

Таблица 2.1

№	Год	Потребительские расходы в расчете на душу населения, тыс. руб., у	Средняя заработная плата и выплаты социального характера, тыс. руб., х
		?	8,0%
		?	12,0%

В качестве исследования сначала выбираем вариант парной линейной эконометрической модели вида:

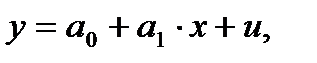
Что же предстоит сделать, чтобы ответить на поставленный в задаче вопрос?

1. Определить форму связи между переменными х и у.

2. Оценить параметры парной линейной регрессии, предполагая, что соблюдаются условия теоремы Гауса-Маркова.

3. Построить график исходной модели и на него «наложить» график полученной парной регрессии.

4. Построить график остатков полученной парной линейной регрессии и по нему определить их характер.

5. Проверить выполнение отдельных условий теоремы Гауса-Маркова: проверить остатки на гомоскедастичность и на автокорреляцию.

6. Оценить тесноту связи между переменными х и у, используя для этого показатели корреляции и детерминации.

7. Оценить силу связи объясняемой переменной с объясняющей с помощью среднего коэффициента эластичности.

8. Оценить с помощью средней ошибки аппроксимации качество полученной регрессии, т.е. отклонение расчетных значений от фактических.

9. Оценить статистическую надежность результатов по полученной регрессии с помощью F – критерия Фишера.

10. Оценить качество полученных параметров парной регрессии.

11. Определить доверительный интервал прогноза для уровня значимости α = 0,5 и проверить полученные параметры регрессии на адекватность.

12. Определить доверительный интервал прогноза для уровня значимости α = 0,5 и проверить полученную регрессию на адекватность.

13. Рассчитать прогнозные значения по графе «Потребительские расходы в расчете на душу населения» в зависимости от средней заработной платы и выплат социального характера на 2014 и 2015 годы.

14. Результаты проведенных исследований следует внести в отчет (см. Приложение 2).

Занятие 1.

1. Коэффициент корреляции r_xy=0.82

2. Форма зависимости между объясняемой y и объясняющей x переменными, если построить график y=f(x) (см. рис. 2.1.), будет нелинейной.

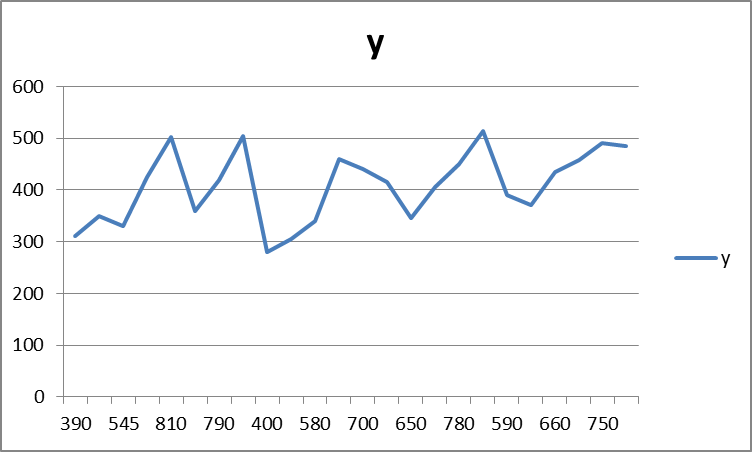
Рисунок 2.1.

3. Расчет параметров парной линейной регрессии.

Для расчета параметров парной линейной регрессии представленной эконометрической модели используем формулы (1.10) и (1.11):

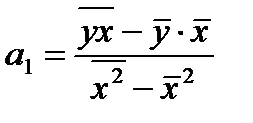
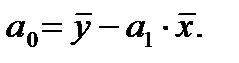
Для этого предварительно рассчитаем следующие значения:

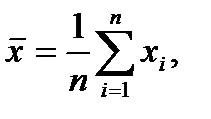
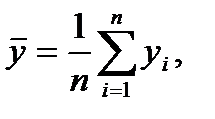
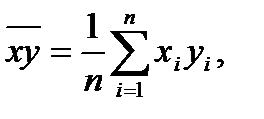
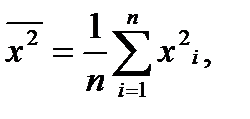
Расчет параметров а₀ и а₁ представлен в таблице 2.2.

В результате расчетов получаем

а₀ = 132,15; а₁ = 0,4186.

Таблица 2.2.

№	Год	y	x	xy	x2
Среднее значение	407,71	658,33	275792,7	451045,8

4. Построим график исходной модели и на него «наложим» график полученной парной линейной регрессии, см. рис. 2.2 (для этого предварительно надо рассчитать оценочные значения 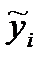, см. табл. 2.3.).

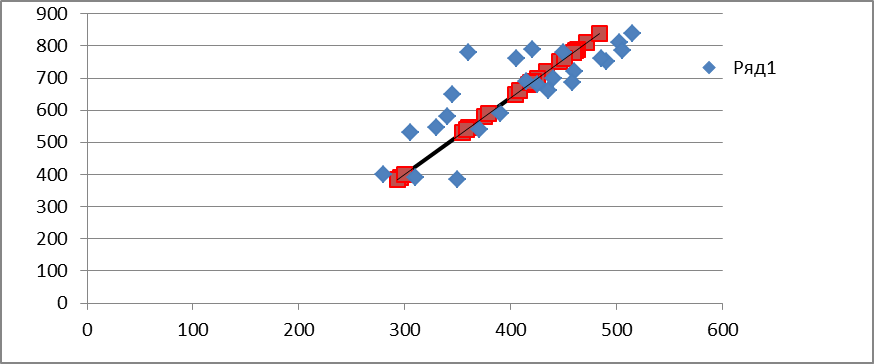
Рисунок 2.2

Таблица 2.3

x	y		E
		295,4	14,6
		293,3	56,7
		360,3	-30,3
		416,8	8,2
		471,2	30,8
		458,6	-98,6
		462,8	-42,8
		460,7	44,3
		299,6	-19,6
		354,0	-49,0
		374,9	-34,9
		433,5	26,5
		425,1	14,9
		421,0	-6,0
		404,2	-59,2
		450,3	-45,3
		458,6	-8,6
		483,7	31,3
		379,1	10,9
		358,2	11,8
		408,4	26,6
		418,9	39,1
		446,1	43,9
		450,3	34,7

5. Построим гистограмму остатков между исходными (статистическими) значениями переменой y и полученными в результате парной линейной регрессии (табл. 2.3, столбец e), см. рис. 2.3.

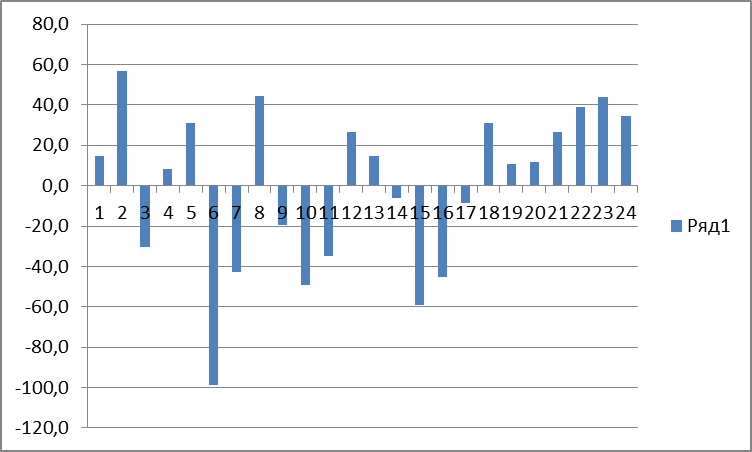
Рисунок 2.3.

По графику остатков можно судить, что они гомоскедастичные.

6. Проведем процедуру оценки параметров регрессионной парной линейной модели. Для этого воспользуемся инструментом Регрессия процедуры Анализ данных табличного процессора Excel, которая будет доступна, если подключить «Пакет анализа». При нажатии в основном меню табличного процессора Excel клавиши Данные становится возможной применение инструментов процедуры Анализ данных.

В высвечиваемом на экране окне Регрессия (см. рис. 2.4) надо внести значения y_i (Входной интервал Y) и значения х_i (Входной интервал Х). Можно также указать параметры вывода или оставить те, какие предлагает программа. После проведенных операций (назначений) нажать на клавишу ОК.

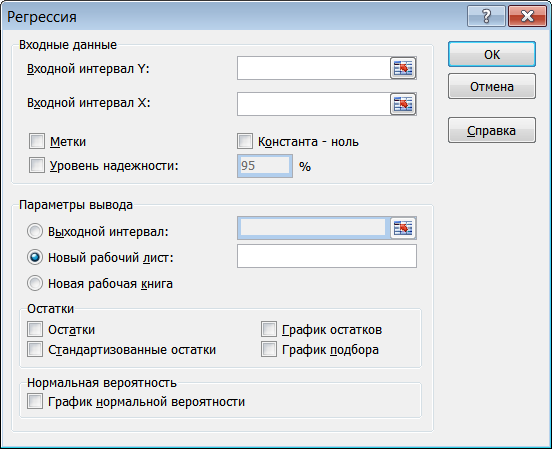
Рисунок 2.4

В результате выполнения инструмента Регрессия на экран дисплея выдается следующая информация, см. рис. 2.5 (результаты приведены для данных рассматриваемой задачи).

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,8202
R-квадрат	0,6728	R2
Нормированный R-квадрат	0,6579
Стандартная ошибка	40,4990	σ
Наблюде-ния
Дисперсионный анализ
	Df	SS	MS	F	Значимо-сть F
Регрессия		74183,235	74183,2359	45,229	9,27E-07
Остаток		36083,723	1640,169
Итого		110266,958
	Коэффициен-ты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересече-ние	132,155	41,799	3,162	0,0045	45,47	218,84
Переменная X1	0,419	0,062	6,725	9,27E-07	0,29	0,5476

Рисунок 2.5

Пояснения к рисунку 2.5[3]:

۰Множественный R – коэффициент корреляции Пирсона, равный корню квадратному из R-квадрат,

۰R-квадрат – коэффициент детерминации, характеризует тесноту связи объясняемой и объясняющих переменных,

۰Наблюдения – количество (n) наблюдений в массиве,

۰ df (Регрессия) – число объясняющих переменных,

۰df (Остаток) – число степеней свободы,

۰df (Итого) – Размер выборки минус 1,

۰SS (Регрессия) – RSS,

۰SS (Остаток) – ESS,

۰SS (Итого) – TSS,

۰F – статистика для оценки связи между объясняемой и объясняющими переменными,

۰Коэффициенты (Y-пересечение) – оценка параметра a₀,

۰Коэффициенты (Переменная X₁) - оценка параметра a₁,

۰Стандартная ошибка (Y-пересечение) – среднеквадратичная ошибка оцененного параметра a₀,

۰Стандартная ошибка (Переменная X₁) - среднеквадратичная ошибка оцененного параметра a₁,

۰t-Статистика (Y-пересечение) – отношение Коэффициент / Стандартная ошибка для параметра a₀,

۰t-Статистика (Переменная X₁) - отношение Коэффициент / Стандартная ошибка для параметра a₁,

۰P-Значение (Y-пересечение) – уровень значимости α для значений t-Статистика для параметра a₀,

۰P-Значение (Переменная X₁) – уровень значимости α для значений t-Статистика для параметра a₁,

۰Верхние и Нижние - границы доверительного интервала для параметров уравнения регрессии, вычисляемые при различных уровнях значимости α.

Сравните полученные значения параметров парной линейной регрессии с рассчитанными ранее по формулам (п.2) данного занятия.

Внимание!

Занятие 2.

Проведем проверку выполнение 2-го и 3-его условия теоремы Гауса-Маркова.

А.Тест Голдфелда-Квандта (тест GQ)

Чтобы проверить 2-е условие теоремы Гауса-Маркова (проверка статистической гипотезы о равенстве дисперсий случайных остатков в наблюдаемых уравнениях Н₀: Var(u₁) = Var(u₂)= …= Var(u_n) = σ_u²) следует провести тест Голдфелда-Квандта, т.е. проверить остатки на гомоскедастичность.

1. Исходные данные для переменных х и у отсортируем по возрастанию значений х, а затем разобьем весь исходный массив из 24 значений на два равных подмассива по 12 значений, см. табл. 2.4.

Таблица 2.4

№	Год	Потребительские расходы в расчете на душу населения, тыс. руб., у	Средняя заработная плата и выплаты социального характера, тыс. руб., х

2. Для первого и второго подмассивов найдем значения ESS (ESS₁ – для первого (верхнего) подмассива из 12 значений, ESS₂ – для второго (нижнего) подмассива из 12 значений). Для этого воспользуемся инструментом Регрессия[4]. Значение ESS₁ берем после проведенных расчетов с первым подмассивом (см. рис. 2.6[5] - выделенная ячейка), а ESS₂ - после проведенных расчетов со вторым подмассивом (см. рис. 2.7 - выделенная ячейка).

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,763172
R-квадрат	0,582431
Нормированный R-квадрат	0,540674
Стандартная ошибка	37,66661
Наблюдения
Дисперсионный анализ
	Df	SS	MS
Регрессия		19789,27	19789,27
Остаток		14187,73	1418,773
Итого

Рисунок 2.6

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,37051
R-квадрат	0,137277
Нормированный R-квадрат	0,051005
Стандартная ошибка	46,48313
Наблюдения
Дисперсионный анализ
	Df	SS	MS
Регрессия		3438,101	3438,101
Остаток		21606,82	2160,682
Итого		25044,92

Рисунок 2.7.

В результате были получены следующие значения:

ESS₁ = 14187,73; ESS₂ = 21606,82,

3. Рассчитаем значения GQ и GQ^-1 по формуле (1.19):

GQ = 0,6566;

GQ^-1 = 1,5229.

4. Для сравнения полученных значений GQ и GQ^-1 с F_крит найдем его значение по таблице 1 Приложения 1 при степени свободы, равной 10, или воспользуемся функцией FРАСПОБР (α; ν₁; ν₂), где ν₁ = ν₂.

FРАСПОБР(0,05;10;10),

F_крит = 2,978

5. Сравним полученные значения GQ и GQ^-1 с значением F_крит по формуле (1.20). Оба значения, т.е. GQ (0,6566) и GQ^-1(1,5229) меньше значения F_крит (2,978). Тем самым подтверждается статистическая гипотеза о равенстве дисперсий случайных остатков в наблюдаемых уравнениях Н₀: Var(u₁) = Var(u₂)= …= Var(u_n) = σ_u²), т.е. остатки обладают гомоскедастичностью.

В. Тест Дарбина – Уотсона (тест DW)

Для проверки 3-его условия теоремы Гауса-Маркова (проверка статистической гипотезы об отсутствии автокорреляции случайных остатков в наблюдаемых уравнениях Н₀: Cov(u_i,u_j) = 0 для всех i ≠ j, следует провести тест Дарбина – Уотсона.

1. Проведем оценку параметров исходной линейной эконометрической модели, используя инструмент Регрессия, см. рис. 2.8. – значения выделены цветом. Получаем следующие оценочные значения параметров линейной парной регрессии:

а₀ = 132,15; а₁ = 0,4186.

2. Для расчета статистики DW по формуле (1.21) проведем расчет числителя, так как знаменатель получается из проведенных расчетов в п.1 подраздела В раздела 2.2. (ESS =36083,723 – выделен цветом на рис. 2.8).

Проведенные расчеты иллюстрируются таблицей 2.5.

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,820
R-квадрат	0,673	R2
Нормированный R-квадрат	0,658
Стандартная ошибка	40,499	Σ
Наблюдения
Дисперсионный анализ
	Df	SS	MS	F
Регрессия		74183,235	74183,235	45,229
Остаток		36083,723	1640,169
Итого		110266,958
	< Наши рекомендации ВВЕДЕНИЕ. Методические указания по выполнению расчетно-графической работы Полонский А.П., Гущин С.В., Введение в профессию. Методические указания по выполнению курсовой работы. € IV. Методические указания студентам по подготовке к занятию. Организационно-методические указания по подготовительной части самостоятельной работы МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ. Методические указания для выполнения контрольной работы по дисциплине «Риторика» для специальностей Введение. Методические указания по выполнению и защите выпускной квалификационной работы бакалавра специальности 050703 – Информационные системы составлены на основании Методические указания по решению задач (в том числе методом «мозгового штурма», методом кейса») И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИХ ИЗУЧЕНИЮ. Методические указания и задания для выполнения контрольной работы по дисциплине «Финансы» для студентов МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ. Введение. На основе результатов выполнения подготовительного этапа курсовой работы и изучения необходимой литературы пишется введение. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ. Методические указания и задания по выполнению домашней контрольной работы для студентов заочного отделения Методические указания по выполнению курсовых работ. Методические указания знакомят студентов с организационной стороной выполнения работы ← Предыдущая страница | Следующая страница →