Задача 2. Расчёт статически определимого ступенчатого бруса

При растяжение (сжатие)

Для статически определимого ступенчатого бруса с жёстко защемлённым концом (см. схемы к задаче 2), нагруженного продольными усилиями Р₁ ,Р₂ , q₁ и q₂ (см. таб. 1.2), необходимо:

1. Построить эпюры продольных сил N, нормальных напряжений s и перемещений .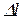

2. Подобрать величину площади поперечных сечений для всех участков бруса из условия прочности по допускаемым нормальным напряжениям при растяжении и сжатии.

Таблица 1.2

№	Р1, кН	Р2, кН	q1, кН/м	q2, кН/м
	10	80	10	70
	20	70	15	80
	30	60	20	90
	40	50	25	60
	50	40	30	50
	60	30	35	40
	70	10	40	30
	80	20	45	20
	10	50	55	50
	20	70	65	20

Принять для всех вариантов следующие соотношения: 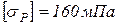, , 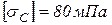Е=10⁵МПа, а=1м.

Схемы к задаче 2

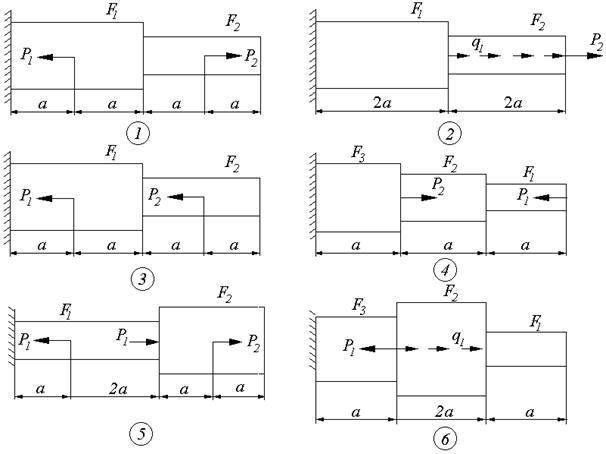
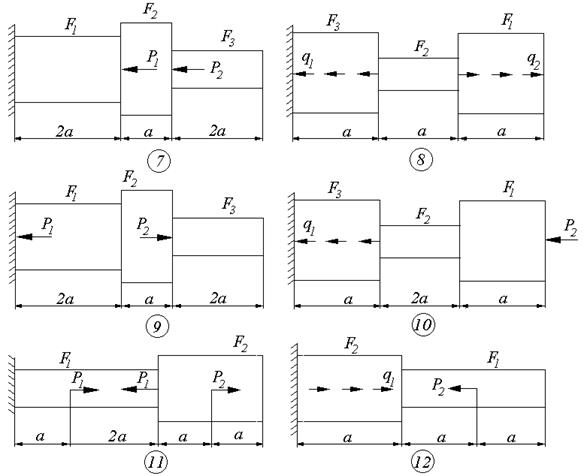
Схемы к задаче 2

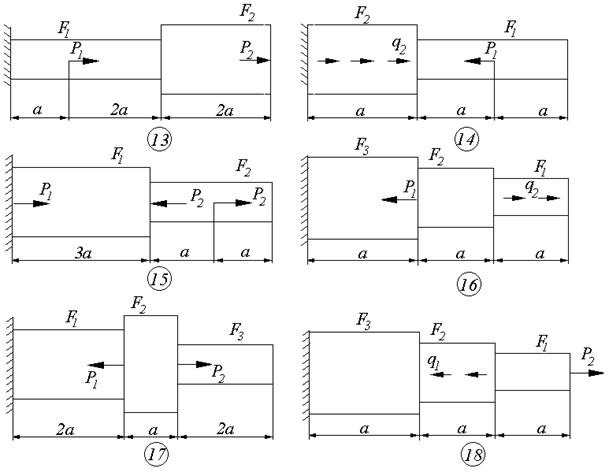
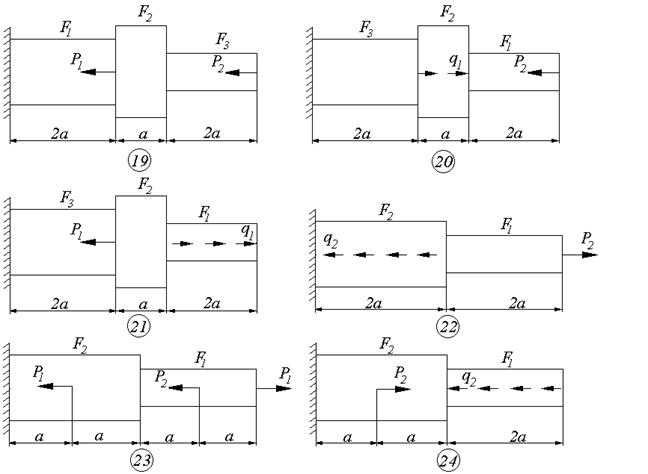
Схемы к задаче 2

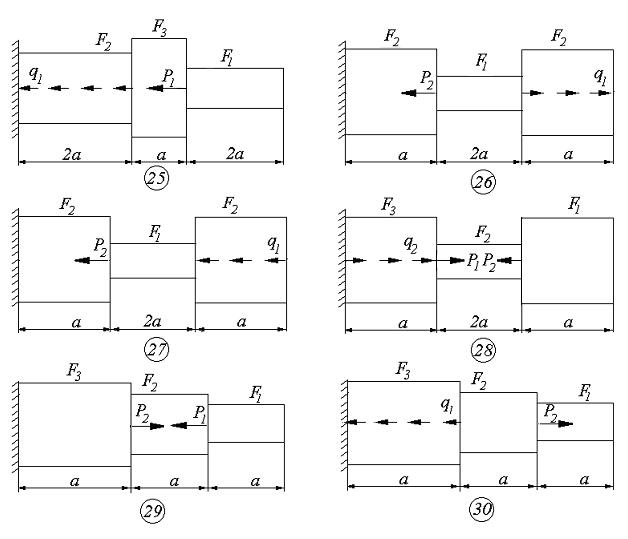
Пример решения задачи 2

Для ступенчатого бруса (см. рис.1.4,а) с жёстко защемлённым концом необходимо:

1. Построить эпюры продольных сил N, нормальных напряжений s и перемещений .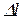

2. Подобрать величину площади поперечных сечений всех участков бруса из условия прочности по нормальным напряжениям, используя следующие числовые значения:

Р₁=30 кН; Р₂=20 кН; q₂=20 кН/м; а=1м; 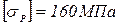; ; 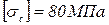Е=1,8×10⁵МПа; F₁=F; F₂=2F; F₃=3F.

Решение

1. Брус состоит из трёх участков. Границами участков являются сечения, к которым приложены внешние силы, или сечения, где изменяются размеры поперечных сечений.

Величину внутренних продольных усилий определим, используя метод сечений. При этом рассматриваем всё время правую отсечённую часть бруса.

Продольную силу N считаем положительной, если нагрузка, её создающая, вызывает растяжение рассматриваемого участка, т.е. направлена от рассматриваемого сечения. Нагрузка, вызывающая сжатие рассматриваемой части бруса, т.е. направленная к сечению, создаёт отрицательную продольную силу. В соответствии с расчётной схемой (рис. 2.1,а) аналитические зависимости для N будут иметь следующий вид:

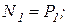
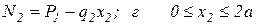тогда

.

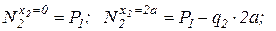
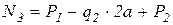После подстановки численных значений, получим:

.

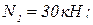
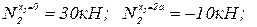
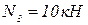На основании полученных значений строим эпюру продольных сил (рис.2.1,б).

Рис. 1.4 Схема нагружения и эпюры N, σ и Δl для ступенчатого

статически определимого бруса

2. Эпюру нормальных напряжений s получим, разделив значения продольной силы N на соответствующие площади поперечных сечений бруса (рис. 1.4,в). Знак продольной силы N определяет и знак соответствующего нормального напряжения s.

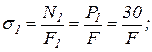
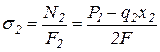, подставляя 2 крайних значения х₂ будем иметь:

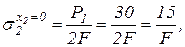
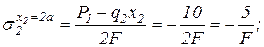
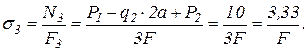
3. Из условия прочности по нормальным наибольшим напряжениям растяжения и сжатия определим параметр F, а затем площади поперечных сечений каждого участка бруса.

Из условия прочности по растягивающим нормальным напряжениям находим:

,

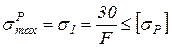отсюда .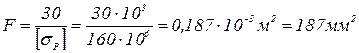

Из условия прочности по сжимающим нормальным напряжениям находим:

,

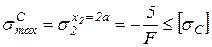отсюда .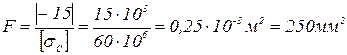

Окончательно выбираем параметр F=250мм².

Определим площади поперечных сечений каждого участка:

F₁=F=250мм², F₂=2F=500мм², F₃=3F=750мм².

3. Зная площади поперечных сечений можно построить эпюру перемещений 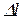(рис.1.4, г). Проще расчёт перемещений вести от заделки, т.е. за точку отсчёта брать сечение, перемещение которого равно 0.

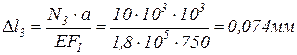
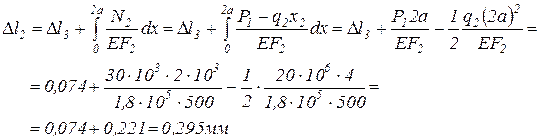
Т.к. уравнение для перемещения на втором участке содержит квадратичную функцию, то графиком функции перемещения на втором участке будет являться парабола, причём в сечении, где 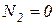парабола будет иметь экстремум. Приравняв уравнение для продольной силы 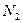к 0, получим расстояние до этого сечения.

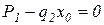
где 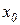- расстояние до сечения, в котором .

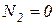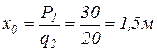
Подставляя, полученное значение для 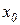, получим значение экстремума на параболе:

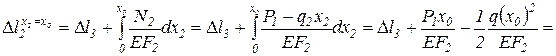
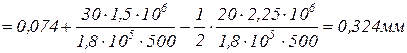
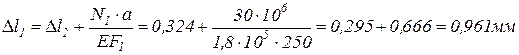
По найденным значениям строим эпюру перемещений (рис.1.4, г).