Учебно-методический комплект

Алгебра 7–9 классы

Учебно-методический комплект

Авторская программа М.Б. Воловича

Пояснительная записка

Курс алгебры 7–9 классов разработан в полном соответствии с ныне действующим образовательным стандартом основного общего образования по математике.

Методическое обеспечение курса представляет собой комплект для 7–9 классов, включающий в себя:

1) учебники для 7, 8 и 9 классов;

2) рабочие тетради к учебникам для 7, 8 и 9 классов;

3) методические рекомендации для учителя «Как обеспечить усвоение алгебры

в 7–9 классах»;

4) дидактические материалы, предназначенные для организации самостоятельных работ в 7, 8 и 9 классах.

Содержание курса представляет собой единое целое с курсом геометрии 7–9 классов: в геометрии широко используются алгебраические методы, в алгебре — сведения, полученные на уроках геометрии.

Курс разработан с позиций внедрения в практику работы школы деятельностного подхода к организации усвоения знаний, умений, навыков, предложенного российскими психологами школы Л.С. Выготского.

Важной особенностью предлагаемой программы является отсутствие в учебнике для 7 класса «повторительного раздела». Повторение, которое эффективно лишь при органичной связи с изучением нового материала, обеспечивается непосредственно в ходе рассмотрения материала того или иного параграфа: предлагаются задания, позволяющие каждому ученику вспомнить ранее изученный материал, необходимый ему для успешного усвоения теории. Поскольку задания в учебнике даны с подробными решениями, они могут быть использованы и для самостоятельной подготовки учащегося.

Еще одной особенностью предлагаемой программы является то, что усвоение обеспечивается только на сознательном уровне. Реализуется принципиально иная, чем в других учебниках схема организации усвоения. В частности, мы полностью отказались от распространенного в учебниках математики «командного» метода изложения доказательств теорем и решения задач, при котором понимание обеспечивается рекомендациями, что и как нужно делать, чтобы получить требуемый результат.

В нашем курсе дается принципиально иной подход к обеспечению понимания: ученики становятся полноправными участниками поиска доказательства теоремы или ответа на вопрос задачи: извлекают информацию из условия, выясняют, какие существуют возможности установить то, что требуется в заключении и т. д.

Предлагаемый комплект реализует не только принципиально иной подход к обеспечению понимания, но и принципиально иную, чем в других учебниках, схему организации усвоения знаний.

Обычно усвоение организуется по следующей схеме:

а) обеспечивается понимание нового материала;

б) понятый материал дети должны выучить;

в) поняв и выучив материал, ученики приступают к решению задач.

Установлено, что гораздо более эффективна другая схема организации усвоения.

а) Обеспечивается проверка готовности учеников к изучению нового материала: проверяется, усвоено ли то из ранее изученного, что является наиболее важным для усвоения новой порции знаний. Выявленные «сбои» немедленно устраняются.

б) Как и при «обычном» обучении, обеспечивается понимание того, что рассказывает учитель. Но это лишь начало процесса, который обозначается у психологов словом «понимание». Во-первых, как уже было сказано, ученики становятся активными участниками поиска ответа на поставленные перед ними вопросы. Во-вторых, непременной составляющей обеспечения понимания является фиксирование самого существенного в новом материале в такой схематической форме, которая позволяет приступить к решению задач, ничего предварительно не заучивая.

в) Очень небольшое число первых заданий (обычно не более трех) выполняется по шагам, с опорой на изучаемую теорию. Правильность выполнения шагов контролируется у каждого ученика.

г) Постепенно пошаговый контроль заменяется самоконтролем.

д) Ученики запоминают новый материал без всякого заучивания, в ходе решения задач.

Предложенная схема может быть реализована в ходе усвоения любой порции материала.

Готовность к изучению нового материала проверяется напоминанием в каждом параграфе учебника ранее изученного, обязательного для предстоящей работы, даются задания с решениями, которые помогают ликвидировать «сбои».

Повторительные упражнения включены в рабочую тетрадь и имеются в методическом пособии. Учитель получает возможность использовать их для эффективного повторение, с учетом специфики каждого класса.

Выполнение нескольких заданий с опорой на изучаемую теорию организуется с помощью рабочей тетради.

Постепенный переход от пошагового контроля к самоконтролю обеспечивается выполнением соответствующих заданий рабочей тетради.

Как правило, в рабочей тетради печатается условие задачи и оставляется место, куда ученик должен вписать решение. Мы разработали принципиально иную рабочую тетрадь: ученики, заполняя пропуски, не могут не проговаривать решение. При этом они не только лучше усваивают материал, но и получают навыки математически грамотной речи. Кроме того, дети приобретают навыки осмысленного чтения. Наконец, в ходе заполнения пропусков с опорой на изучаемые теоретические сведения новый материал запоминается.

Обеспечить «проговаривание» всего хода оперирования с новыми знаниями каждым учеником при обычном обучении просто невозможно. Поэтому мы искали (и нашли!) эквивалент проговаривания всеми учениками в классе при выполнении первых заданий самого главного в изучаемом материале. Заполняя пропуски в рассуждениях, ученики проговаривают эти рассуждения. Все сбои и ошибки могут быть выявлены и исправлены сразу же.

Существенной особенностью представленной авторской программы является то, что осуществляется обучение не только новым знаниям, но и способам работы с ними. Например, организуя поиск доказательства, мы учим не только рассматриваемому конкретному доказательству, но и общим подходам к поиску решения задач и доказательству теорем: «разворачиванию» условия; «разворачиванию» заключения; умению замкнуть цепочку рассуждений.

Кроме того, целенаправленно обеспечивается пропедевтическое знакомство с материалом, который будет изучаться в дальнейшем.

Разрабатывая программу, мы стремились обеспечить развивающее обучение не столько за счет введения новых для 7–9 класса тем, сколько за счет более эффективной методики организации учебного процесса. Курс строится таким образом, чтобы максимально обеспечить развивающее обучение. Эта цель декларируется во многих ныне действующих пособиях. Мы ценим (и реализуем в нашем комплекте) такие компоненты развивающего обучения, как стремление обеспечить самостоятельность детей при знакомстве с новыми знаниями, предъявление большого числа творческих (для учеников) задач. Однако наши подходы к обеспечению развивающего обучения качественно отличаются от имеющихся на сегодняшний день в учебниках математики. Перечислим некоторые наиболее важные отличия.

1) Как и в других развивающих программах, содержание предлагаемого курса существенно обогащено включением нестандартных задач, которые посильны лишь наиболее подготовленным учащимся. Но, предлагая такие задания и рекомендуя учителю всячески поощрять тех, кто с ними справился, мы обязательно включаем в комплект материал, который поможет большинству учеников в классе научиться решать такие задачи. Кроме того, мы подготавливаем учеников к решению многих задач повышенной трудности, выстраивая «цепочки» таких задач, в которых предыдущие готовят учеников к решению следующих. Таким образом, обеспечено систематическое и планомерное обучение решению нестандартных задач. Это удается осуществить за счет того, что на обучение решению задач обязательного минимума в нашем курсе требуется значительно меньше времени, чем при традиционном обучении благодаря принципиально иному, чем в других комплектах, методическому подходу.

2) Обеспечивается обучение общим способам работы с новыми знаниями, что существенно облегчает усвоение материала в следующих классах. Например, общим способам работы с определениями, поиском доказательств теорем и решения задач.

3) Формируется самостоятельность школьников в ходе изучения нового материала и решения задач (в частности, за счет широкого использования заданий «с пропусками»).

4) Максимально обеспечивается реализация принципа сознательности обучения.

5) Максимально обеспечивается уровневая дифференциация в ходе обучения. Во-первых, включенные в учебник задания четко делятся на 4 группы:

задачи обязательного минимума, выполнение которых является достаточным условием удовлетворительного усвоения материала параграфа;

задачи немного более сложные, решение которых обеспечивает хорошие знания;

задачи достаточно трудные, решение которых свидетельствует об отличном усвоении материала;

задачи повышенной сложности, необходимые для того, чтобы учитывались интересы наиболее интересующихся математикой и подготовленных детей.

Во-вторых, самостоятельные работы в дидактических материалах включают 4 задачи обязательного минимума (это дает шанс учиться успешно более слабым ученикам, которые усвоили новый материал, но имеют пробелы в ранее изученном), задачу более трудную (позволяющую ученикам осознать, что материал ими усвоен действительно хорошо) и задачу повышенной трудности. Если ученик справился с шестой задачей, он поощряется дополнительной пятеркой. При этом около половины задач повышенной трудности в действительности не так уж трудны, они лишь необычно для учеников сформулированы. Это позволяет каждому решить хотя бы некоторые из таких задач.

ПРОГРАММА

Класс

(3 ч в неделю,всего102 ч)

Решение системы двух уравнений первой степени с двумя неизвестными графическим способом, методом подстановки и методом алгебраического сложения. Решение задач методом составления систем уравнений — (12 ч).

О с н о в н а я ц е л ь — научить решать системы двух уравнений первой степени с двумя неизвестными и использовать полученные навыки при решении задач.

Знакомство с графическим методом важно, во-первых, для того чтобы повторить и закрепить навыки построения графика линейной функции и «считывания» информации после построения графика, во-вторых, чтобы ученики осознали: решением системы уравнений является не число, к чему они уже привыкли, а упорядоченная пара чисел. Однако основное внимание при обучении решению систем уравнений уделяется способам подстановки и сложения. Важно, чтобы учащиеся осознали: все операции, которые выполняются в ходе решения исходной системы, приводят к рассмотрению новой системы, решения которой такие же, как у исходной. В ходе решения можно лишь переходить от одной системы двух уравнений с двумя неизвестными к новой системе, имеющей те же решения.

Класс

(3 ч в неделю,всего 102 ч)

Числовые неравенства и их свойства. Сложение и умножение числовых неравенств. Двойные неравенства. Числовые промежутки. Неравенства первой степени с одним неизвестным. Решение системы неравенств первой степени с одним неизвестным — (24 ч).

О с н о в н а я ц е л ь — обеспечить усвоение свойств числовых неравенств и умение решать неравенства первой степени с одним неизвестным и системы таких неравенств, сознательно пользуясь этими свойствами.

Изучение темы начинается с повторения геометрического смысла числовых неравенств: возможности сравнивать числа с помощью числовой прямой. Вводится новый способ сравнения с помощью отыскания разности чисел, который является теоретической основой при доказательстве свойств неравенств. Вместе с тем, при доказательстве теорем, решении неравенств и их систем используется в качестве графической иллюстрации сравнение чисел с помощью числовой прямой.

Свойства неравенств используются для обоснования того, что в ходе решения неравенства каждый раз получается неравенство, имеющее те же решения, что и исходное.

Вводятся понятия числового промежутка, двойного неравенства, числового отрезка, луча, интервала, которые важны не только при решении неравенств и их систем, но и для успешного усвоения функциональной линии всего курса алгебры.

В связи с решением систем неравенств, рассматриваются примеры решения простейших неравенств, содержащих модуль неизвестного. Формирование умения решать такие неравенства не предусматривается.

2. Четные и нечетные функции. Функции у = 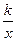и у = kх²,их графики и свойства — (15 ч).

О с н о в н а я ц е л ь — сформировать понятие четной и нечетной функции, познакомить с особенностями графиков таких функций, научить использовать эти особенности при построении графиков функцийу = 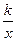и у = kх²; опираясь на графики, сформулировать свойства этих функций.

Изучение темы начинается с того, что вводятся понятия четной и нечетной функций, среди функций, с которыми ученики к этому времени познакомились, выявляются четные и нечетные, формулируется гипотеза о наличии у графиков таких функций центральной или осевой симметрии, доказываются соответствующие теоремы.

Выявленные особенности графиков, а также умение осуществлять их преобразование позволяет осуществить построение графиков, а затем выявить другие свойства рассматриваемых функций.

Осуществляется знакомство с графиками дробно-линейных функций. Формирование умения строить такие графики не предусматривается.

При изучении темы формируются умения определять по графику промежутки возрастания и убывания функции, промежутки знакопостоянства и нули функции. Осуществляется на интуитивно-наглядном уровне знакомство с понятием асимптоты, понятиями наибольшего и наименьшего значения функции.

3. Квадратное уравнение. Графическое решение квадратного уравнения. Квадратичная функция у = ах² + bx +c и ее график — (5 ч).

О с н о в н а я ц е л ь — сформировать понятие квадратного уравнения; познакомить с возможностью находить корни квадратного уравнения, построив параболу и прямую; познакомить с возможностью построить графикфункции у = ах² + bx +c, выполняя геометрические преобразования графикафункции у = х².

Определение квадратного уравнения позволяет сформулировать и доказать теорему о том, что любое квадратное уравнение может быть заменено приведенным квадратным уравнением, имеющим те же корни, что исходное уравнение. Это позволяет свести графическое решение квадратного уравнения к построению параболы у = х² и прямой.

Выделение полного квадрата при построении графикафункции у = ах² + bx +c готовит учеников к отысканию формулы, позволяющей решить любое квадратное уравнение, повторяя при этом многое из ранее изученного.

4. Действительные числа. Функция у = 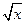и ее график — (8 ч).

О с н о в н а я ц е л ь — систематизировать сведения о рациональных числах; дать представление об иррациональных числах; познакомить с понятием взаимно обратных функций, с особенностями графиков взаимно обратных функций, с функцией у = 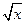и ее графиком.

Сведения о рациональных числах, имеющиеся у учеников, пополнены лишь теоремами, позволяющими утверждать, что число, которое нельзя представить в виде бесконечной периодической десятичной дроби, не является рациональным числом. Выполненное в задании доказательство того, что существуют числа, квадрат которых равен например 7, и что среди рациональных чисел их нет, является теоремой существования не рациональных (иррациональных) чисел. Кроме того, введены обозначения для всех известных ученикам множеств чисел. Эти обозначения не подлежат заучиванию: они запомнятся в ходе работы.

В рассматриваемой теме осуществляется лишь первоначальное знакомство со взаимно обратными функциями и особенностями их графиков. Поэтому главное здесь — обеспечить понимание того, при каком условии для рассматриваемой функции можно получить обратную, умение выполнить замену у на х и х на у в исходной функции, умение перейти от записи х = у² к записи у = 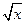и наоборот, умение перейти от записи у = 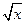к записи х = у² и найти значение у, соответствующее указанному значению х.

5. Арифметический квадратный корень и его свойства. Преобразование выражений, содержащих квадратные корни — (12 ч).

О с н о в н а я ц е л ь — обеспечить усвоение понятия арифметического квадратного корня и свойств арифметического квадратного корня; научить в простейших случаях освобождаться от иррациональности в знаменателе; получить первоначальное представление о преобразовании выражений, содержащих квадратные корни.

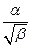Основное внимание следует уделять преобразованиям, связанным с непосредственным применением определения арифметического квадратного корня, теорем о корне из произведения и дроби, использованию тождества = |а|, вынесению множителя из-под знака корня и внесению множителя под знак корня, освобождению от иррациональности в знаменателе выражений вида и .

6. Квадратные уравнения: решение неполных квадратных уравнений; решение квадратных уравнений выделением полного квадрата; формула корней квадратного уравнения вида ах² + bx + c = 0; соотношения между корнями квадратного уравнения и его коэффициентами; равносильные и неравносильные преобразования уравнений; решение задач — (20 ч).

О с н о в н а я ц е л ь — обеспечить понимание вывода формулы корней квадратного уравнения вида ах² + bx + c = 0, умение решать квадратные уравнения, простейшие рациональные уравнения и применять их к решению задач.

Решение неполных квадратных уравнений и решение квадратных уравнений выделением полного квадрата — подготовка к выводу формулы корней квадратного уравнения вида ах² + bx + c = 0. Не следует специально заниматься решением квадратных уравнений, выделением полного квадрата. Основное внимание следует уделять решению квадратных уравнений, пользуясь формулой.

Материал, связанный с теоремой Виета и обратной ей, носит вспомогательный характер. Доказательство этих теорем не относится к обязательному материалу.

При рассмотрении дробных рациональных уравнений особенно важно сделать предметом сознания учеников исключение посторонних корней.

Алгоритм решения задач остается тем же, что и в предыдущих классах. Но аппарат уравнений, используемый для решения текстовых задач, существенно расширяется.

Класс

(3 ч в неделю, всего 102 ч)

Уравнения и системы уравнений второй степени: уравнения, приводимые к квадратным; иррациональные уравнения; уравнения с модулями; решение систем уравнений второй степени; решение задач с помощью систем уравнений второй степени — (20 ч).

О с н о в н а я ц е л ь — познакомить с решением методом разложения на множители и введения вспомогательной переменной уравнений с одним неизвестным, степень которых выше второй; выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными; и текстовые задачи с помощью составления таких систем.

Данная тема завершает изучение рациональных уравнений с одной переменной. Учащиеся знакомятся с решением некоторых уравнений, степень которых больше 2, с помощью разложения на множители и введения вспомогательной переменной.

В данной теме вводится понятие иррационального уравнения и алгоритмы, позволяющие решить простейшие такие уравнения.

Продолжается обучение решению уравнений, содержащих модуль неизвестного. Учащиеся знакомятся с решением систем, включающих уравнения и неравенства. Осуществляется закрепление и углубление знакомства с методом интервалов.

Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Основное внимание уделяется системам, в которых одно уравнение первой степени, а другое — уравнение второй степени. Известный учащимся способ подстановки позволяет свести решение такой системы к решению квадратного уравнения. Решение уравнений второй степени с двумя неизвестными, в которых оба уравнения второй степени, не является обязательным материалом.

3. Арифметическая и геометрическая прогрессии: способы задания последовательностей; формула n-го члена арифметической и геометрической прогрессий; формула суммы первых n членов арифметической и геометрической прогрессий; сумма бесконечной геометрической прогрессии, у которой |q| < 1; задачи на прогрессии — (28 ч).

О с н о в н а я ц е л ь — дать представление о числовых последовательностях и способах их задания; сформировать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида; научить пользоваться формулами для вычисления n-го члена и суммы первых n членов арифметической и геометрической прогрессий.

Последовательность вводится как функция f(n), заданная на любой части множества натуральных чисел. Рассматриваются различные способы задания последовательностей. Особое внимание уделяется рекуррентному способу задания и выработке умения использовать индексные обозначения.

При выводе формул для вычисления n-го члена арифметической и геометрической прогрессий дается первоначальное представление о методе полной математической индукции.

Сведения о бесконечно убывающей геометрической прогрессии не являются обязательными для изучения.

4. Степень с рациональным показателем: степенные функции вида у = хⁿ;график уравнения окружности; графическое решение уравнений и систем уравнений; корни третьей и четвертой степени. Понятие о корне n-ой степени из числа; арифметический корень n-ой степени из числа и его свойства; степени с дробным показателем и их свойства; тождественные преобразования выражений, содержащих корни и степени — (16 ч).

О с н о в н а я ц е л ь — дать представление о степенных функциях и их графиках; о графическом решении уравнений и систем уравнений, степень которых выше первой; познакомить с понятиями корня n-ой степени из числа, степени с дробным показателем и их свойствами.

При знакомстве с графиками степенных функций и их свойствами самое главное — повторить и закрепить уже известные ученикам сведения о свойствах функций и особенностей их графиков. Доказательства теорем о четности или нечетности степенных функций, о возрастании или убывании степенных функций не являются обязательными.

График уравнения окружности дается в рассматриваемой теме потому, что умение строить окружность расширяет возможности графического решения уравнений и систем уравнений.

Знакомство с понятием корня n-ой степени из числа можно ограничить обеспечением понимания той связи, которая существует между функциями у = 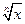и у = хⁿ и между соответствующими графиками обратных функций.

Свойства корней n-ой степени из числа — материал не обязательный.

Усвоению подлежит определение степени с дробным показателем 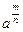. Достаточно, чтобы ученики понимали: свойства любых степеней с рациональными показателями такие же, как свойства степеней с натуральными показателями. Доказательство этого факта — материал не обязательный.

Алгебра 7–9 классы

Авторская программа М.Б. Воловича

Пояснительная записка

Курс алгебры 7–9 классов разработан в полном соответствии с ныне действующим образовательным стандартом основного общего образования по математике.

Содержание курса представляет собой единое целое с курсом геометрии 7–9 классов: в геометрии широко используются алгебраические методы, в алгебре — сведения, полученные на уроках геометрии.

Кроме того, целенаправленно обеспечивается пропедевтическое знакомство с материалом, который будет изучаться в дальнейшем.

Разрабатывая программу, мы стремились обеспечить развивающее обучение не столько за счет введения новых для 7–9 класса тем, сколько за счет более эффективной методики организации учебного процесса. Курс строится таким образом, чтобы максимально обеспечить развивающее обучение. Эта цель декларируется во многих ныне действующих учебниках математики. Однако наши подходы к обеспечению развивающего обучения качественно отличаются от имеющихся.

Как и в других развивающих программах, содержание предлагаемого курса существенно обогащено включением нестандартных задач, которые посильны лишь наиболее подготовленным учащимся. Но, предлагая такие задания, мы обязательно включаем в комплект материал, который поможет большинству учеников в классе научиться решать такие задачи. Это удается осуществить за счет того, что на обучение решению задач обязательного минимума в нашем курсе требуется значительно меньше времени, чем при традиционном обучении благодаря принципиально иному, чем в других комплектах, методическому подходу.

Существенной особенностью представленной авторской программы является то, что осуществляется обучение не только новым знаниям, но и способам работы с ними. Например, организуя поиск доказательства, мы учим не только рассматриваемому конкретному доказательству, но и общим подходам к поиску решения задач и доказательству теорем: «разворачиванию» условия; «разворачиванию» заключения; умению замкнуть цепочку рассуждений.

Таким образом обеспечивается обучение общим способам работы с новыми знаниями, что существенно облегчает усвоение материала в следующих классах.

На изучение алгебры в 7 классе отводится несколько меньше времени, чем обычно: более компактное изложение материала в нашем учебнике 7 класса позволило перераспределить время между курсами алгебры и геометрии.

Программой предусмотрено изучать каждый параграф алгебры в 7–9 классах в течении четырех уроков, что является «средней» величиной. На изучение каких-то параграфов может потребоваться два-три урока. На изучение каких-то может не хватить четырех. В этом случае можно воспользоваться «резервными» уроками.

М.Б. Волович

Алгебра 7–9 классы

Учебно-методический комплект

Авторская программа М.Б. Воловича

Пояснительная записка

Курс алгебры 7–9 классов разработан в полном соответствии с ныне действующим образовательным стандартом основного общего образования по математике.

Методическое обеспечение курса представляет собой комплект для 7–9 классов, включающий в себя:

1) учебники для 7, 8 и 9 классов;

2) рабочие тетради к учебникам для 7, 8 и 9 классов;

3) методические рекомендации для учителя «Как обеспечить усвоение алгебры

в 7–9 классах»;

4) дидактические материалы, предназначенные для организации самостоятельных работ в 7, 8 и 9 классах.

Содержание курса представляет собой единое целое с курсом геометрии 7–9 классов: в геометрии широко используются алгебраические методы, в алгебре — сведения, полученные на уроках геометрии.

Курс разработан с позиций внедрения в практику работы школы деятельностного подхода к организации усвоения знаний, умений, навыков, предложенного российскими психологами школы Л.С. Выготского.

Важной особенностью предлагаемой программы является отсутствие в учебнике для 7 класса «повторительного раздела». Повторение, которое эффективно лишь при органичной связи с изучением нового материала, обеспечивается непосредственно в ходе рассмотрения материала того или иного параграфа: предлагаются задания, позволяющие каждому ученику вспомнить ранее изученный материал, необходимый ему для успешного усвоения теории. Поскольку задания в учебнике даны с подробными решениями, они могут быть использованы и для самостоятельной подготовки учащегося.

Еще одной особенностью предлагаемой программы является то, что усвоение обеспечивается только на сознательном уровне. Реализуется принципиально иная, чем в других учебниках схема организации усвоения. В частности, мы полностью отказались от распространенного в учебниках математики «командного» метода изложения доказательств теорем и решения задач, при котором понимание обеспечивается рекомендациями, что и как нужно делать, чтобы получить требуемый результат.

В нашем курсе дается принципиально иной подход к обеспечению понимания: ученики становятся полноправными участниками поиска доказательства теоремы или ответа на вопрос задачи: извлекают информацию из условия, выясняют, какие существуют возможности установить то, что требуется в заключении и т. д.

Предлагаемый комплект реализует не только принципиально иной подход к обеспечению понимания, но и принципиально иную, чем в других учебниках, схему организации усвоения знаний.

Обычно усвоение организуется по следующей схеме:

а) обеспечивается понимание нового материала;

б) понятый материал дети должны выучить;

в) поняв и выучив материал, ученики приступают к решению задач.

Установлено, что гораздо более эффективна другая схема организации усвоения.

а) Обеспечивается проверка готовности учеников к изучению нового материала: проверяется, усвоено ли то из ранее изученного, что является наиболее важным для усвоения новой порции знаний. Выявленные «сбои» немедленно устраняются.

б) Как и при «обычном» обучении, обеспечивается понимание того, что рассказывает учитель. Но это лишь начало процесса, который обозначается у психологов словом «понимание». Во-первых, как уже было сказано, ученики становятся активными участниками поиска ответа на поставленные перед ними вопросы. Во-вторых, непременной составляющей обеспечения понимания является фиксирование самого существенного в новом материале в такой схематической форме, которая позволяет приступить к решению задач, ничего предварительно не заучивая.

в) Очень небольшое число первых заданий (обычно не более трех) выполняется по шагам, с опорой на изучаемую теорию. Правильность выполнения шагов контролируется у каждого ученика.

г) Постепенно пошаговый контроль заменяется самоконтролем.

д) Ученики запоминают новый материал без всякого заучивания, в ходе решения задач.

Предложенная схема может быть реализована в ходе усвоения любой порции материала.

Готовность к изучению нового материала проверяется напоминанием в каждом параграфе учебника ранее изученного, обязательного для предстоящей работы, даются задания с решениями, которые помогают ликвидировать «сбои».

Повторительные упражнения включены в рабочую тетрадь и имеются в методическом пособии. Учитель получает возможность использовать их для эффективного повторение, с учетом специфики каждого класса.

Выполнение нескольких заданий с опорой на изучаемую теорию организуется с помощью рабочей тетради.

Постепенный переход от пошагового контроля к самоконтролю обеспечивается выполнением соответствующих заданий рабочей тетради.

Как правило, в рабочей тетради печатается условие задачи и оставляется место, куда ученик должен вписать решение. Мы разработали принципиально иную рабочую тетрадь: ученики, заполняя пропуски, не могут не проговаривать решение. При этом они не только лучше усваивают материал, но и получают навыки математически грамотной речи. Кроме того, дети приобретают навыки осмысленного чтения. Наконец, в ходе заполнения пропусков с опорой на изучаемые теоретические сведения новый материал запоминается.

Обеспечить «проговаривание» всего хода оперирования с новыми знаниями каждым учеником при обычном обучении просто невозможно. Поэтому мы искали (и нашли!) эквивалент проговаривания всеми учениками в классе при выполнении первых заданий самого главного в изучаемом материале. Заполняя пропуски в рассуждениях, ученики проговаривают эти рассуждения. Все сбои и ошибки могут быть выявлены и исправлены сразу же.

Существенной особенностью представленной авторской программы является то, что осуществляется обучение не только новым знаниям, но и способам работы с ними. Например, организуя поиск доказательства, мы учим не только рассматриваемому конкретному доказательству, но и общим подходам к поиску решения задач и доказательству теорем: «разворачиванию» условия; «разворачиванию» заключения; умению замкнуть цепочку рассуждений.

Кроме того, целенаправленно обеспечивается пропедевтическое знакомство с материалом, который будет изучаться в дальнейшем.

Разрабатывая программу, мы стремились обеспечить развивающее обучение не столько за счет введения новых для 7–9 класса тем, сколько за счет более эффективной методики организации учебного процесса. Курс строится таким образом, чтобы максимально обеспечить развивающее обучение. Эта цель декларируется во многих ныне действующих пособиях. Мы ценим (и реализуем в нашем комплекте) такие компоненты развивающего обучения, как стремление обеспечить самостоятельность детей при знакомстве с новыми знаниями, предъявление большого числа творческих (для учеников) задач. Однако наши подходы к обеспечению развивающего обучения качественно отличаются от имеющихся на сегодняшний день в учебниках математики. Перечислим некоторые наиболее важные отличия.

1) Как и в других развивающих программах, содержание предлагаемого курса существенно обогащено включением нестандартных задач, которые посильны лишь наиболее подготовленным учащимся. Но, предлагая такие задания и рекомендуя учителю всячески поощрять тех, кто с ними справился, мы обязательно включаем в комплект материал, который поможет большинству учеников в классе научиться решать такие задачи. Кроме того, мы подготавливаем учеников к решению многих задач повышенной трудности, выстраивая «цепочки» таких задач, в которых предыдущие готовят учеников к решению следующих. Таким образом, обеспечено систематическое и планомерное обучение решению нестандартных задач. Это удается осуществить за счет того, что на обучение решению задач обязательного минимума в нашем курсе требуется значительно меньше времени, чем при традиционном обучении благодаря принципиально иному, чем в других комплектах, методическому подходу.

2) Обеспечивается обучение общим способам работы с новыми знаниями, что существенно облегчает усвоение материала в следующих классах. Например, общим способам работы с определениями, поиском доказательств теорем и решения задач.

3) Формируется самостоятельность школьников в ходе изучения нового материала и решения задач (в частности, за счет широкого использования заданий «с пропусками»).

4) Максимально обеспечивается реализация принципа сознательности обучения.

5) Максимально обеспечивается уровневая дифференциация в ходе обучения. Во-первых, включенные в учебник задания четко делятся на 4 группы:

задачи обязательного минимума, выполнение которых является достаточным условием удовлетворительного усвоения материала параграфа;

задачи немного более сложные, решение которых обеспечивает хорошие знания;

задачи достаточно трудные, решение которых свидетельствует об отличном усвоении материала;

задачи повышенной сложности, необходимые для того, чтобы учитыва