Свойства функций (четность, нечетность, периодичность)

9.1.Определите, какой из ниже приведенных графиков соответствует

четной функции (нечетной функции). Выберите ответ и кратко поясните, почему.

9.2.Проверьте, является ли четной или нечетной функция, заданная формулой:

1) g(х) = (sinх)² + 5х⁶

2) f(х) = 2х³ + 8x

3) k(х) = 5х² + 3х + 5

9.3.Проверьте, является ли четной или нечетной функция, заданная формулой:

1) g(х) = cos(3x)

2) f(х) = 2sin2 х

3) k(х) = 0,5х³ + 3х⁵

9.4. Исследуйте функцию на четность.

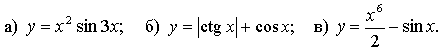
9.5. Исследуйте функцию на четность.

9.6.Определить, периодична ли функция, указать ее наименьший период

а) б) в)

9.7. Определить, периодична ли функция, указать ее наименьший период

6) у = sin2х + tg х/2

в) у = cos х/3 + tg х/5.

а) у = 3sin(х-2)+7cosπх.

9.8. Определить, периодична ли функция, указать ее наименьший период

а) у = 3cos4x; б) у = sin(-2x); в) у = tg2х.

9.9. Определить, периодична ли функция, указать ее наименьший период

а) у = sinx + tgх;

б) у = sin2x + cosх;

в) у = |cosx|.

9.10. Указать график четной периодической функции

9.11. Указать график нечетной периодической функции

9.12. Указать график четной непериодической функции

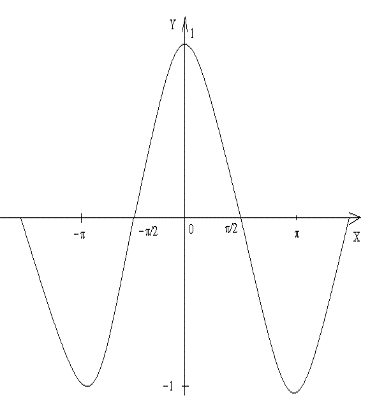
9.13. Указать график нечетной непериодической функции

9. 14. Указать график непериодической функции

9.15. Достроить график так, чтобы функция была бы периодична, указать наименьший период

9.16. Найдите множество значений функции:

9.17. Найдите множество значений функции:

9.18. Найдите множество значений функции:

9.19. Найдите множество значений функции:

9.20. Сколько целых чисел содержится в области определения функции

9.21.Сколько целых чисел содержится в области определения функции

9.22. Сколько целых чисел содержится в области определения функции

9.23. Сколько целых чисел содержит область определения функции

9.24. Найти наибольшее и наименьшее значения функции

на отрезке .

9.25. Функция определена на всей числовой прямой и является четной. На рисунке изображен график этой функции при . Найдите .

9.26. Функция определена на всей числовой прямой и является нечетной. На рисунке изображен график этой функции при . Найдите .

Чтение графика функции

Используя график функции у = f(x) (см. рис. ниже), определите и запишите ответ

10.1. Промежутки возрастания и убывания функции.

11.1. При каких значениях x .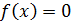

12.1. Наибольшее и наименьшее значения функции.

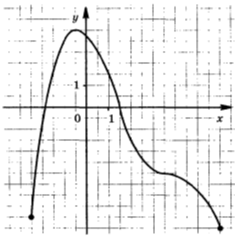
10.2. Промежутки возрастания и убывания функции.

11.2. Наибольшее и наименьшее значения функции.

12.2. При каких значениях x .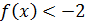

10.3. Промежутки, на которых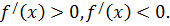

11.3. Точки экстремума функции.

12.3. Наибольшее и наименьшее значения функции.

10.4. Нули функции.

11.4. Промежутки возрастания и убывания функции.

12.4. Наибольшее и наименьшее значения функции.

10.5. При каких значениях x функция y не имеет производной.

11.5. При каких значениях x выполняется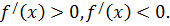

12.5. Наибольшее и наименьшее значения функции.

10.6. При каких значениях x выполняется .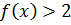

11.6. Промежутки возрастания и убывания функции.

12.6. При каких значениях x .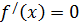

10.7. При каких значениях x выполняется ?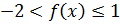

11.7. Промежутки возрастания и убывания функции.

12.7. При каких значениях x .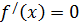

10.8. Область определения функции.

11.8. При каких значениях x выполняется .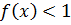

12.8. При каких значениях x выполняется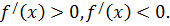

10.9. Область определения функции.

11.9. При каких значениях x выполняется .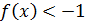

12.9. При каких значениях x выполняется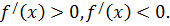

10.10. Область определения функции.

11.10. При каких значениях x выполняется .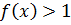

12.10. Промежутки возрастания и убывания функции.

10.11. Область определения функции.

11.11. При каких значениях x выполняется .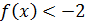

12.11. Промежутки возрастания и убывания функции.

10.12. Область определения функции.

11.12. При каких значениях x выполняется .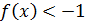

12.12. Промежутки возрастания и убывания функции

.

10.13. Область определения функции.

11.13. При каких значениях x выполняется .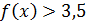

12.13. При каких значениях x выполняется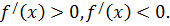

10.14. При каких значениях x выполняется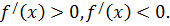

11.14. При каких значениях x выполняется .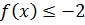

12.14. Наибольшее и наименьшее значения функции.

10.15. Область определения функции.

11.15. При каких значениях x выполняется .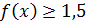

12.15. При каких значениях x выполняется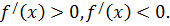

10.16. При каких значениях x выполняется .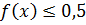

11.16. Промежутки возрастания и убывания функции.

12.16. Наибольшее и наименьшее значения функции.

10.17. При каких значениях x выполняется .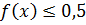

11.17. Точки экстремума функции.

12.17. Промежутки возрастания и убывания функции.

10.18. При каких значениях x выполняется .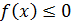

11.18. Промежутки возрастания и убывания функции.

12.18. Наибольшее и наименьшее значения функции.

10.19. Область определения функции.

11.19. При каких значениях x выполняется .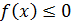

12.19. Точки экстремума функции.

10.20. При каких значениях x выполняется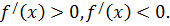

11.20. При каких значениях x выполняется .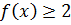

12.20. Наибольшее и наименьшее значения функции.

Призмы

13.1. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 45°. Найдите боковое ребро параллелепипеда.

13.2. Основанием прямого параллелепипеда является ромб с диагоналя­ми 10 см и 24 см, а высота параллелепипеда равна 10 см. Найдите большую диагональ параллелепипеда.

13.3. В правильной треугольной призме сторона основания равна 10 см и высо­та равна 15 см. Вычислите площади боковой и полной поверхности приз­мы.

13.4. В правильной четырехугольной призме сторона основания равна 12 дм и высо­та равна 8 дм. Вычислите площади боковой и полной поверхности приз­мы.

13.5. В правильной шестиугольной призме сторона основания равна 23 см и высо­та равна 5 дм. Вычислите площади боковой и полной поверхности приз­мы.

13.6. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см³ воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см³.

13.7. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 10.

13.8. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 15, а площадь полной поверхности равна 930.

13.9. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы.

13.10. В сосуд, имеющий форму правильной треугольной призмы, налили 1300 см³ воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 28 см. Найдите объем детали. Ответ выразите в см³.

13.11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 18 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого? Ответ выразите в сантиметрах.

13.12. Площадь поверхности правильной треугольной призмы равна 19. Какой будет площадь поверхности призмы, если все ее ребра увеличить в семь раз?

13.13. Площадь поверхности правильной четырехугольной призмы равна 20. Какой будет площадь поверхности призмы, если все ее ребра увеличить в пять раз?

13.14. Классное помещение должно быть таким, чтобы на одного учащегося приходилось не менее 6 м³ воздуха. Можно ли в кабинете с параметрами a=8,5 м, b=6 м, c=3,6 м заниматься с 30 учащимися, не нарушая санитарной нормы?

13.15. Какое количество кирпича сможет перевезти машина, имеющая размеры кузова 3,7м*2,2м*0,8м? Размеры кирпича 25см*12см*8см.