Движение жидкости и газа в пласте и скважине

Движение жидкости и газа в пласте и скважине

Методические указания и задания к курсовой работе

по дисциплине «Гидравлика и нефтегазовая гидромеханика»

Содержание

ВВЕДЕНИЕ.. 4

1 ВЫБОР ВАРИАНТА ЗАДАНИЯ.. 5

1.1 ВЫБОР ФЛЮИДА.. 5

1.2 ВЫБОР ОБЛАСТИ ДВИЖЕНИЯ.. 6

1.3 ВЫБОР РАСПОЛОЖЕНИЯ СКВАЖИНЫ.. 8

1.4 ВЫБОР НЕОДНОРОДНОСТИ ПЛАСТА.. 9

1.5 НЕСОВЕРШЕНСТВО СКВАЖИН.. 11

1.6 ПОСТАНОВКА ЗАДАЧИ.. 12

2 ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ДВИЖЕНИЯ ЖИДКОСТИ И ГАЗА В СКВАЖИНЕ 16

2.1 УРАВНЕНИЕ БЕРНУЛЛИ.. 16

2.2 УРАВНЕНИЕ НЕРАЗРЫВНОСТИ.. 17

2.3 ПОТЕРИ НАПОРА ПО ДЛИНЕ. 18

2.4 ПОТЕРИ НАПОРА НА МЕСТНЫХ СОПРОТИВЛЕНИЯХ.. 19

2.5 ПОТЕРИ НАПОРА В НЕКРУГЛЫХ ТРУБАХ.. 20

2.6 ДВИЖЕНИЕ ГАЗА ПО ТРУБАМ.. 21

2.7 ПОРЯДОК РАСЧЕТА.. 23

3 УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ И ГАЗА В ПОРИСТОЙ СРЕДЕ 25

3.1 ОСНОВНЫЕ ПОНЯТИЯ.. 25

3.2 ЗАКОН ДАРСИ.. 26

3.3 РАСЧЕТ ДЕБИТА СКВАЖИНЫ.. 27

3.4 НЕСОВЕРШЕННЫЕ СКВАЖИНЫ.. 28

3.5 НЕОДНОРОДНЫЙ ПЛАСТ. 29

3.6 ИНТЕРФЕРЕНЦИЯ СКВАЖИН.. 31

3.7 ФИЛЬТРАЦИЯ ГАЗА.. 35

3.8 ПОРЯДОК РАСЧЕТА.. 37

4 ОФОРМЛЕНИЕ КУРСОВОЙ РАБОТЫ... 39

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 43

Введение

Методические указания предназначены для студентов дневной и заочной форм обучения специальности 21.03.01 «Нефтегазовое дело» и ставят своей целью познакомить студента с основами расчета движения жидкости и газа в трубах и пористой среде на примере расчета курсовой работы по дисциплине «Подземная гидромеханика». Методические указания составлены в соответствии с программой и учебными планами.

Для правильного понимания процессов, происходящих при движении нефти и газа, нефтяник должен знать особенности движения нефти и газа в пласте и скважине, а также влияние свойств пласта на продуктивность скважины. Поэтому курсовая работа представляет собой комплексную задачу, рассматривающую совместную работу пласта и скважины. В результате выполнения курсовой работы студент должен найти дебит скважины и предложить способы его увеличения.

1 Выбор варианта задания

Вариант задания курсовой работы и численные данные выбирается по двум последним цифрам зачетной книжки. Подчеркиванием ()выделены значения для варианта задания с двумя последними цифрами зачетной книжки - 16. Величины, взятые из таблиц при расчетах, необходимо перевести в систему единиц СИ.

ВЫбор флюида

Выбор флюида (нефть или газ) осуществляется по последней цифре зачетной книжки.

Если последняя цифра четная, то происходит движение нефти. Свойства нефти и некоторые параметры скважины:

r - плотность нефти, кг/м³;

m - динамическая вязкость нефти, мПа·с;

L - глубина скважины, м;

р_к - пластовое давление на контуре питания, МПа;

p_у - давление на устье, МПа;

D_ш - диаметр отверстия в штуцере, мм.

Эти величины выбираются по предпоследней цифре из таблицы 1.1.

Таблица 1.1 – Исходные данные

Предпоследняя цифра		1
r, кг/м3		715
m, мПа·с		3
L, м		925
pк, МПа		11
pу, МПа	0,1	0,2	0,3	0,4	0,5	0,4	0,3	0,2	0,1	0,2
Dш, мм		15

Если последняя цифра нечетная, то происходит движение газа. Свойства газа и некоторые параметры скважины:

r_ат - плотность газа при атмосферном давлении, кг/м³;

m - динамическая вязкость газа, мПа·с;

L - глубина скважины, м;

p_к - пластовое давление на контуре питания, МПа;

p_у - давление на устье, МПа.

Эти величины выбираются по предпоследней цифре из таблицы 1.2.

Таблица 1.2 – Исходные данные

Предпоследняя цифра
rат, кг/м3	0,72	0,74	0,75	0,77	0,79	0,81	0,82	0,83	0,85	0,86
m, мПа·с	0,006	0,007	0,008	0,011	0,013	0,010	0,018	0,019	0,021	0,025
L, м
pк, МПа
pу, МПа	3,4	8,1	13,1

Пластовую температуру t_п приблизительно можно рассчитать, зная глубину залегания пласта (глубину скважины L) по формуле t_п =ω_п·L, где ω_п - геотермический градиент (принять равным 0,02°С/м).

Выбор области движения

Выбор области движения осуществляется по предпоследней цифре зачетной книжки. Если предпоследняя цифра четная, то движение происходит внутри насосно-компрессорных труб (НКТ).

Геометрические параметры:

D_в - внутренний диаметр НКТ, мм;

L_нкт - длина НКТ, м;

D_зв - внутренний диаметр замка НКТ, мм;

Δ - шероховатость стенок НКТ, мм;

D_ок - внутренний диаметр обсадной колонны, мм;

D_с - диаметр скважины, мм.

Эти величины выбираются по последней цифре из таблицы 1.3.

Таблица 1.3 – Исходные данные

Последняя цифра
Dв, мм	50,3	62,0	59,0	75,9	72,9	88,6	100,3	50,3	62,0	59,0
Lнкт, м			5,5	6,5	7,5	8,5	9,5		5,5	8,5
Dзв, мм	48,3	60,0	57,0	73,9	70,9	86,6	98,3	48,3	60,0	57,0
Δ, мм	0,5	0,1	0,17	0,21	0,32	0,39	0,46	0,27	0,61	0,15
Dок, мм	190,7	193,7	196,3	198,7	201,3	203,7	205,7	190,7	193,7	196,3
Dс, мм	219,1	219,1	219,1	219,1	219,1	219,1	219,1	219,1	219,1	219,1

Если предпоследняя цифра нечетная, то движение происходит между насосно-компрессорных труб (НКТ) и обсадной колонной.

Геометрические параметры:

D_н - наружный диаметр НКТ, мм;

L_нкт - длина НКТ, м;

D_зн - наружный диаметр замка НКТ, мм;

Δ - шероховатость стенок, мм;

D_ок - внутренний диаметр обсадной колонны, мм;

D_с - диаметр скважины, мм.

Эти величины выбираются по последней цифре из таблицы 1.4.

Таблица 1.4 – Исходные данные

Последняя цифра							6
Dн, мм	60,3	73,0	73,0	88,9	88,9	101,6	114,3	60,3	73,0	73,0
Lнкт, м			5,5	6,5	7,5	8,5	9,5		5,5	8,5
Dзн, мм	71,0	84,0	86,0	102,0	104,0	116,0	130,0	71,0	84,0	86,0
Δ, мм	0,75	0,6	0,57	0,41	0,32	0,39	0,36	0,23	0,1	0,15
Dок, мм	190,7	193,7	196,3	198,7	201,3	203,7	205,7	190,7	193,7	196,3
Dс, мм	219,1	219,1	219,1	219,1	219,1	219,1	219,1	219,1	219,1	219,1

Замечание. В случае движения газа наружный и внутренний диаметры замка НКТ не потребуются.

Выбор расположения скважины

Выбор расположения скважины производится по двум последним цифрамзачетной книжки по таблице 1.5.

Таблица 1.5 – Исходные данные

Две последние цифры	Номер рисунка
00, 08, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96	1.1
01, 09, 17, 25, 33, 41, 49, 57, 65, 73, 81, 89, 97	1.2
02, 10, 18, 26, 34, 42, 50, 58, 66, 74, 82, 90, 98	1.3
03, 11, 19, 27, 35, 43, 51, 59, 67, 75, 83, 91, 99	1.4
04, 12, 20, 28, 36, 44, 52, 60, 68, 76, 84, 92	1.5
05, 13, 21, 29, 37, 45, 53, 61, 69, 77, 85, 93	1.6
06, 14, 22, 30, 38, 46, 54, 62, 70, 78, 86, 94	1.7
07, 15, 23, 31, 39, 47, 55, 63, 71, 79, 87, 95	1.8

На рисунках обозначено:

a - расстояние от скважины до прямолинейного контура питания или непроницаемой границы, м (рисунки 1.1 - 1.6);

b - расстояние от скважины до прямолинейного контура питания или непроницаемой границы, м (рисунки 1.3 - 1.6);

R_к - расстояние от скважины до контура питания, м;

R_б - расстояние от угла до скважины, м (рисунки 1.7 - 1.8).

Численные значения выбираются по последней цифре из таблицы 1.6.

Таблица 1.6 – Исходные данные

Последняя цифра							6
a, м							200
b, м							250
Rк, м							650
Rб, м							150

Схемы расположения скважин

Рисунок 1.1 Рисунок 1.2 Рисунок 1.3

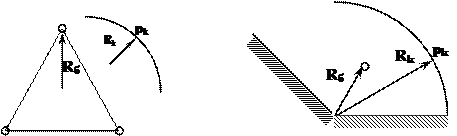Рисунок 1.4 Рисунок 1.5 Рисунок 1.6

Рисунок 1.7 Рисунок 1.8

На рисунке 1.7 скважины расположены по сторонам равностороннего треугольника и одинаковы. На рисунке 1.8 угол между непроницаемыми границами 120˚ и скважина находится в средине этого угла.

Выбор неоднородности пласта

Выбор вида неоднородности пласта осуществляется по предпоследней цифре зачетной книжки. Если предпоследняя цифра 0 ‑ 4, то пласт неоднородный по толщине.

Параметры неоднородности:

N - число пропластков, (пропластки нумеруются сверху вниз);

k_i - проницаемость i - того пропластка, мкм² (1 мкм² = 10^{-12 м2});

h_i - толщина i - того пропластка, м.

Численные значения выбираются по последней цифре из таблицы 1.7.

Таблица 1.7 – Исходные данные

Последняя цифра							6
N							4
ki, мкм2	0,25   0,45	0,37   0,15   0,43	0,27   0,18   0,32   0,20	0,22   0,11   0,08   0,05   0,15	0,37   0,55	0,25   0,08   0,33	0,38 0,29 0,43 0,31	0,31   0,21   0,17   0,11   0,27	0,32   0,45	0,27   0,15   0,43
hi, м	2,0   3,0	1,5   4,0   2,0	4,0   3,2   2,2   1,8	3,5   5,0   6,0   7,0   4,2	5,5   6,5	2,5   5,0   3,8	6,0 6,2 4,2 3,8	6,5   8,0   11,0   17,0   7,2	25,0   30,0	15,5   14,0   12,0

Если предпоследняя цифра 5 ‑ 9, то пласт зонально-неоднородный.

Параметры неоднородности:

N - число зон, (зоны нумеруются от скважины);

k_i - проницаемость i - той зоны, м²;

R_i - внешний радиус i - той зоны, м;

h - толщина пласта, м.

Численные значения выбираются по последней цифре из таблицы 1.8.

Таблица 1.8 – Исходные данные

Последняя цифра
N
ki, мкм2	0,15   0,55	0,07   0,15   0,43	0,70   0,40   0,32   0,20	0,02   0,11   0,18   0,25   0,35	0,5   0,35	0,67   0,55   0,43	0,17   0,28   0,32   0,42	0,48   0,31   0,28   0,22   0,15	0,45   0,14	0,27   0,35   0,48
Ri, м	1,0   Rк	0,5   2,0   Rк	0,4   1,2   2,2   Rк	0,35   0,8   1,3   2,5   Rк	0,5   Rк	1,5   2,7   Rк	0,6   1,2   3,2   Rк	0,3   1,8   2,9   8,0   Rк	1,9   Rк	0,9   4,0   Rк
h, м	5,2	7,8	11,3	13,5	16,8	20,4	22,7	24,1	25,9	31,2

Замечание. Внутренний радиус первой зоны R_o равен радиусу скважины r_c и равен половине диаметра скважины D_c, который задан в разделе 1.2.

Несовершенство скважин

Скважина считается несовершенной по степени и характеру вскрытия. Показатели несовершенства по степени вскрытия:

= b/h - степень вскрытия пласта или пропластка;

h - толщина рассматриваемого пласта или пропластка, м;

b - вскрытая часть рассматриваемого пласта или пропластка, м.

Показатели несовершенства по характеру вскрытия:

l_п - длина перфорационного канала, см;

d_п - диаметром перфорационного канала, см;

n_п - число перфорационных отверстий на один метр скважины, отв./м.

Численные значения выбираются по последней цифре из таблицы 1.9.

Таблица 1.9 – Исходные данные

Последняя цифра							6
, %							70
lп, cм							2
dп, cм	1,0	1,2	1,4	1,6	1,8	2,0	1,0	1,2	1,4	1,6
nп, отв./м							20

Постановка задачи

По выбранным данным рисуем схемы расположения скважины в соответствии с вариантом. При построении схемы масштаб не соблюдается, но проставляются значения всех геометрических параметров. Графическая часть выполняется в виде рисунков и графиков на миллиметровке, кальке или компьютере. Ниже приведен пример задания и схема к нему (вариант №16).

Скважина радиусом r_c = D_c/2 = 219,1/2 = 109,5 мм = 0,109 м пробурена на глубину L = 925 м и вскрывает нефтяной горизонтальный пласт с круговым контуром питания на расстоянии R_k = 650 м от скважины, толщиной h = 6,0 + 6,2 + 4,2 + 3,8 = 20,2 м . В пласте и скважине происходит однофазное установившееся движение. Давление на контуре р_k = 11 МПа, давление на устье р_у = 0,2 МПа. Вязкость и плотность флюида в пластовых условиях равны, соответственно, m = 3 мПа·с = 3 10^-3 Па·с, r = 715 кг/м³, эквивалентная шероховатость стенок скважины и труб Δ = 0,36 мм = 0,36 10^{-3 м.}

В соответствии с вариантом задания необходимо учесть следующие пункты (некоторые из них могут отсутствовать): А, Б, В, Г, Д, Е, Ж, З.

А. В скважину спущена колонна насосно-компрессорных труб (НКТ) с наружным диаметром D_н = 114,3 мм = 0,114 м. Нефть движется по кольцевому пространству между НКТ и стенкой обсадной колонны.

Б. Местными сопротивлениями являются замки в местах соединения труб. Наружный диаметр замка D_зн = 130 мм, длина трубы L_нкт = 9,5 м. Диаметр штуцера D_ш = 15 мм.

В. Пласт является зонально-неоднородным и имеет N = кольцевых зон с различными проницаемостями k_i = и различными радиусами кольцевых зон R_i = . Этого пункта в данном варианте НЕТ.

Г. Пласт является неоднородным по толщине и имеет N = 4 пропластка, изолированных друг от друга с проницаемостями k_i = 0,38; 0,29; 0,43; 0,31 мкм² и толщинами h_i = 6,0; 6,2; 4,2; 3,8 м. Очевидно, что h = h₁ + h₂ + h₃ + h₄ = 20,2 м.

Д. Скважина несовершенна по степени вскрытия и вскрывает нижний, четвертый, пропласток на глубину b/h₄ = 70 % = 0,7.

Е. Скважина несовершенна по характеру вскрытия, т.к. по всей вскрытой толщине пласта имеет n_п = 20 отверстий на один погонный метр толщины пласта диаметром d_п = 1,0 см. Глубина проникновения перфорационного канала в породу l_п = 2 см.

Ж. На расстоянии a = 200 м от скважины находится прямолинейный контур питания.

На рисунке 1.1 показана схема притока и движения флюида в скважине (третий пропласток не показан). На рисунке 1.2 показана схема расположения скважины в пласте. На этих рисунках цифрами обозначены: 1 - стенка скважины; 2 - колонна труб НКТ; 3 - перфорационные отверстия; 4 - первый пропласток; 5 – штуцер; 6 – пакер; 7 - прямолинейный контур питания; 8 - удаленный контур питания.

При составлении схем следует внимательно следить за соответствием схемы заданию на курсовую работу, т.к. ошибки в схемах приведут к дальнейшим ошибкам в расчетах.

1 – стенка скважины;

2 – колонна труб;

3 – перфорационные отверстия;

4 - первый пропласток.

Рисунок 1.1 - Схема притока и движения флюида в скважине

1 – скважина;

7 – прямолинейный контур питания;

8 – удаленный контур питания.

Рисунок 1.2 - Схема расположения скважины в пласте

Уравнение Бернулли

Для применения уравнения Бернулли необходимо выбрать плоскость сравнения (обозначается 0-0). Плоскостью сравнения может служить любая горизонтальная плоскость. Также необходимо выбрать два сечения. Сечения проводятся перпендикулярно вектору скорости. Нумерация сечений производится по направлению движения жидкости. Уравнение Бернулли для установившегося движения реальной несжимаемой жидкости записывается [1]:

(2.1)

где z - расстояние от плоскости сравнения до центра тяжести сечения. Если сечение лежит ниже плоскости сравнения, то z отрицательно;

p - абсолютное или манометрическое давление в сечениях;

r - плотность несжимаемой жидкости;

α - коэффициент кинетической энергии. Обычно принимается равным единице;

v - средняя скорость в сечениях;

g - ускорение свободного падения;

h_1-2 - потери напора между сечениями 1 и 2. Они представляют собой сумму потерь напора по длине и сумму потерь напора на местных сопротивлениях

(2.2)

На схеме (рисунок 1.1) плоскость сравнения удобно выбрать по поверхности земли, сечение 1-1 у кровли пласта, а сечение 2-2 за штуцером. Тогда z₁ = - L, z₂ = 0, т.к. z₂ << z₁, р₁ = р_з, р₂ = р_у. Скоростными напорами α₁v₁²/2g и α₂v₂²/2g пренебрегаем, т.к. они малы по сравнению с потерями напора по длине. Из формулы (2.1) найдем давление у кровли пласта:

р_з = р_y + rg (L + h_1-2). (2.3)

Уравнение неразрывности

Уравнение неразрывности является следствием закона сохранения массы. Если поток ограничен непроницаемыми стенками, то при установившемся движении масса жидкости или газа, прошедшая через любое сечение потока за одно и то же время, будет одинакова. Поэтому массовый расход Q_m постоянен Q_m = const. Массовый расход связан с объемным расходом Q и средней скоростью v с отношениями:

Q_m = r Q = r ω v = const, (2.4)

где r - плотность газа;

ω - площадь поперечного сечения.

В общем случае при движении сжимаемой жидкости и газа плотность и объемный расход меняются по длине потока, т.к. давление по длине потока падает, а соответственно падает плотность газа и увеличивается объемный расход.

Часто вместо массового расхода при движении газа рассматривают приведенный к нормальным условиям объемный расход Q_am.

Q_am = Q_m/r_am = Q r/r_am . (2.5)

При движении несжимаемой жидкости (r = const), уравнение неразрывности (2.4) упрощается:

Q_m/r = Q = v w = const. (2.6)

Поэтому исходя из уравнения неразрывности при известном массовом расходе, плотности и площади поперечного сечения потока, можно найти среднюю скорость движения в поперечном сечении

v = Q_m/r w , (2.7)

а для несжимаемой жидкости

v = Q/w . (2.8)

Потери напора по длине

Потери напора по длине определяются по формуле Дарси-Вейсбаха:

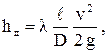(2.9)

где ℓ - длина трубы (или участка трубы) на котором определяются потери напора;

D – диаметр трубы;

v - средняя скорость в трубе;

λ = λ(Re, Δ/D)- коэффициент гидравлического сопротивления трения. Коэффициент гидравлического сопротивления трения зависит от двух безразмерных параметров Re - числа Рейнольдса и Δ/D - относительной шероховатости трубы.

Число Рейнольдса определяется по формуле:

Re = v D r/μ = v D/ν , (2.10)

где μ - динамическая вязкость жидкости, Па с;

ν - кинематическая вязкость жидкости, м²/с.

Для определения коэффициента гидравлического сопротивления трения существует много различных формул. Удобно пользоваться следующими формулами.

Для ламинарного режима движения:

λ = 64/Re, если Re < 2000. (2.11)

Для турбулентного режима движения:

λ = 0,11 (68/Re + Δ/D)^0.25 , если Re > 2000. (2.12)

Движение газа по трубам

Малые перепады давлений. Если перепад давления мал, т.е. (р₁ - р₂)/р₁ = 0,1, то в этом случае с точностью до 10% можно сжимаемостью газа пренебречь и расчет вести как для несжимаемой жидкости. Для расчета необходимо найти среднее давление р_ср в колонне труб, среднюю температуру Т_ср, среднее значение коэффициента сверхсжимаемости z_ср (для идеального газа z_ср = 1). Так как давление на забое скважины неизвестно, то в первом приближении давление на забое скважины можно принять равным пластовому. Считая температуру газа на поверхности равной 20°С (293°К), а пластовую температуру Т_пл, получим:

р_ср = 0,5 (р_у + р_з), Т_ср = 0,5 (293 + Т_пл). (2.20)

Движение газа считается изотермическим, поэтому средняя плотность идеального газа находится как

ρ_ср = ρ_ат р_ср Т_ат/(р_ат Т_ср). (2.21)

где р_ат - атмосферное давление, принимается равным 0,1 МПа;

ρ_ат - плотность газа при стандартных условиях;

Т_ат - стандартных температура (293°К).

Объемный расход, приведенный к среднему значению давления и температуры в скважине, определится по формуле

Q = Q_ат ρ_ат /ρ_ср , (2.22)

а средние скорости движения газа

v = Q/w. (2.23)

Дальнейший расчет ведется аналогично расчету движения несжимаемой жидкости. По окончании расчета будет найдено в первом приближении давление на забое скважины. После этого найдем уточненное значение среднего давления и средней плотности газа по формулам (2.20, 2.21) и в ходе расчета найдем новое значение забойного давления. Таким образом, дальнейшие расчеты продолжать до тех пор, пока значение старого и нового забойного давления будут отличаться не более чем на 1%.

Большие перепады давлений. Если перепад на забое и устье большой, т.е. (р₁ - р₂)/р₁ > 0,1, то в этом случае удобно пользоваться формулой Адамова. Для расчета необходимо найти среднее давление р_ср в колонне труб, среднюю температуру Т_ср, среднее значение коэффициента сверхсжимаемости z_ср (для идеального газа z_ср = 1). Так как давление на забое скважины неизвестно, то в первом приближении давление на забое скважины можно принять равным пластовому. Считая температуру газа на поверхности равной 20°С (293°К), а пластовую температуру Т_пл получим

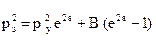, (2.24)

здесь

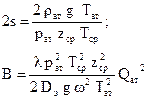(2.25)

Коэффициент гидравлического сопротивления трения рассчитывается по формулам раздела 2.3, только число Рейнольдса удобнее рассчитывать по формуле:

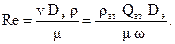(2.26)

Порядок расчета

1). Задаемся максимальными значениями расхода. Расход (дебит) нефтяных и газовых скважин зависит от диаметра труб, перепада давления, вязкости, проницаемости пласта и многих других причин. Поэтому максимально возможные значения расхода (дебита) данной скважины задать, даже ориентировочно, трудно. Например, на Усинском месторождении дебит нефтяных скважин составляет от 10 до 100 м³/сут. Для газовых скважин значение приведенного дебита, например, на Вуктыльском месторождении, порядка 10⁵ м³/сут.

2). При заданном максимальном расходе (дебите) определяют среднюю скорость движения жидкости (газа) (п. 2.2), число Рейнольдса (п. 2.3), коэффициент гидравлического сопротивления трения (п. 2.3), коэффициент местных сопротивлений, потери напора и находят значение давления на забое скважины. При расчете движения газа в скважине, порядок расчета определения забойного давления определяется согласно пункту 2.6.

3). Задаемся значениями расхода (дебита), которые составляют 0,8; 0,6; 0,4; 0,2 и 0 от максимального значения расхода (дебита). Расчет производится аналогично пункту 2).

4). Результаты расчета удобно оформить в виде таблицы (таблица 2.2). В столбце примечаний указываются значения коэффициентов местных сопротивлений, вязкости жидкости, плотности газа при атмосферных условиях.

5). На основании расчетов строится зависимость забойного давления от расхода (рисунок 3.3).

Таблица 2.1 – Результаты расчетов

№№ по п.п.	Расход Q	Плотность ρ (ρат)	Скорость v = Q/ω	Число Рейнольдса Re	Режим движения	Коэффициент гидравлического сопротивления трения λ	Потери напора между сечениями 1 и 2 h1-2	Забойное давление Pз	Примечание
	м3/с	кг/м3	м/с	-	-	-	м	МПа
1.
2.
3.
4.
5.
6.

Замечание. Нулевое значение расхода берется обязательно.

Основные понятия

Пористая среда представляет собой множество твердых частиц пространство между которыми (поры, трещины) заполнено жидкостью или газом [2]. Коэффициентом пористости m называется отношение объема пор в образе W_п к объему образца W:

m = W_п/W . (3.1)

Просветностью n называется отношение площади просветов w_п в поперечном сечении образца к площади поперечного сечения этого образца:

n = w_п/w, (3.2)

Можно доказать, что средняя просветность равна пористости. Жидкость в образце породы движется только по порам, поэтому при известном объемном расходе жидкости (газа) действительная скорость движения частиц жидкости v равна:

v = Q/w_п , (3.3)

Удобно ввести фиктивную скорость, которую назовем скоростью фильтрации u. Эта скорость соответствует движению жидкости, как через поры образца, так и через породу. Поэтому при том же объемном расходе через образец, скорость фильтрации определяется:

u = Q/w . (3.4)

Скорость фильтрации связана с действительной скоростью соотношением

u = m v. (3.5)

Из сравнения формулы для скорости фильтрации (3.4) и формулы для движения жидкости по трубам (2.7) видно, что они имеют один и тот же вид, т.к. закон сохранения массы справедлив и при фильтрации жидкости (газа), то уравнение неразрывности при фильтрации жидкости будет иметь тот же вид, что и при движении жидкости по трубам.

Для жидкости и газа:

Q_m = r w u = const (3.6)

Для несжимаемой жидкости (r = const(p)) это уравнение упрощается:

Q = w u = const (3.7)

Закон Дарси

Движение однородной жидкости пористой среде определяется силами давления и силами тяжести. Основное соотношение теории фильтрации - закон Дарси - устанавливает связь между величиной скорости фильтрации вдоль линии тока и силами, действующими в жидкости, и записывается:

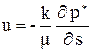, (3.8)

где u - скорость фильтрации вдоль линии тока;

k - коэффициент проницаемости, который характеризует свойства породы;

m - динамический коэффициент вязкости;

¶s - расстояние между двумя бесконечно близкими точками линии тока;

¶p^* - перепад приведенных давлений в этих точках.

Приведенное давление зависит от давления в данной точке, плотности жидкости r, ускорения силы тяжести g, расстояния z от плоскости сравнения до данной точки и определяется:

p^* = p + r g z. (3.9)

При движении жидкости в горизонтальных пластах (z = const), второе слагаемое постоянно и при подстановке в формулу (3.9) обращается в нуль. Поэтому в горизонтальных пластах при движении однородной жидкости приведенное давление можно положить равным давлению в данной точке.

При больших скоростях движения жидкости, особенно часто это касается газа, происходит нарушение закона Дарси. В этом случае необходимо пользоваться нелинейными законами фильтрации.

Расчет дебита скважины

Если скважина вскрывает пласт на всю толщину пласта h и фильтрация происходит по всей боковой поверхности, то скважина называется совершенной. Поперечные сечения представляют собой боковую поверхность цилиндра радиусом r и высотой h. Поэтому площадь поперечного сечения равна:

w = 2 p r h. (3.10)

При движении несжимаемой жидкости удобно пользоваться уравнением неразрывности в виде:

Q = u w = const. (3.11)

Частицы жидкости к скважине движутся от контура питания по радиусам. Поэтому радиусы являются линиями тока и расстояние вдоль линии тока удобно отсчитывать от радиуса контура питания Rk. Оно будет равно:

S = R_k - r, dS = -dr. (3.12)

Тогда закон Дарси (3.8) запишется в виде:

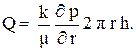(3.13)

Используя соотношения (3.10) и (3.11), последнее уравнение легко интегрируется. Если заданы давления на контуре питания p_k и на скважине p_з, и известен радиус скважины r_c, то дебит (расход), скважины находится по формуле Дюпюи:

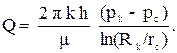(3.14)

Практически давление на скважине совпадает с забойным давлением, которое рассчитывается во второй главе (p_c = p_з).

Несовершенные скважины

Если скважина вскрывает пласт не на всю толщину, а на некоторую глубину b, то скважина называется несовершенной по степени вскрытия. При этом b/h называется относительным вскрытием пласта.

Если скважина сообщается с пластом не по всей боковой поверхности, а только через специальные отверстия, то такую скважину называют несовершенной по характеру вскрытия. Дебит несовершенных скважин определяется по формуле

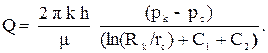(3.15)

где С₁, С₂ - безразмерные коэффициенты.

Эти коэффициенты удобно определять по графикам В.И. Щурова или аналитическим зависимостям, которые приведены в [3, 4].

Коэффициент С₁ учитывающий дополнительное фильтрационное сопротивление в призабойной зоне пласта из-за несовершенства скважины по степени вскрытия зависит только от относительного вскрытия пласта h и отношения толщины пласта к диаметру скважины h/D_с.

Коэффициент С₂ учитывающий дополнительное фильтрационное сопротивление в призабойной зоне пласта из-за несовершенства скважины по характеру вскрытия зависит от диаметра перфорационного канала d_п, числа отверстий на один погонный метр длины скважины n_п и длины перфорационного канала l_п. По следующим безразмерным параметрам определяются:

l_п/D_c – график, по которому находится С₂ ,

d_п/D_c – номер линии на этом графике;

n_п D_c – значение С₂.

В отличие от С₁, С₂ может принимать отрицательные значения, что приводит при прочих равных условиях к увеличению дебита скважины. Удобно ввести понятие о приведенном радиус r’_c, т.е. радиус такой совершенной скважины, дебит которой равен дебиту данной несовершенной скважины:

r’_c = r_c exp(-(С₁ + С₂)). (3.16)

Тогда формула (3.14) запишется в виде:

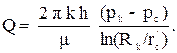(3.17)

Неоднородный пласт

Часто встречаются пласты, значительные области которых сильно отличаются друг от друга по фильтрационным характеристикам. Можно выделить два основных вида неоднородностей такого типа - это слоисто - неоднородные и зонально - неоднородные пласты. Слоисто - неоднородный пласт состоит из пропластков разной толщины h_i и проницаемости k_i. Часто пропластки разделены непроницаемыми границами. В других случаях между ними существуют перетоки. В случае непроницаемых границ между пропластками, каждый пропласток можно считать, как отдельный пласт, со своей проницаемостью, толщиной и дебитом Q_i. Поэтому дебит скважины в таком пропластке будет определяться по формуле Дюпюи:

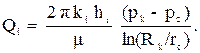(3.18)

А дебит всей скважины будет равен сумме дебитов всех пропластков:

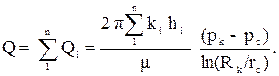(3.19)

Если заменить слоисто - неоднородный пласт однородным с проницаемостью k_ср таким образом, что дебиты слоисто - неоднородного и однородного пласте были равны, тогда среднюю проницаемость можно определить по формуле:

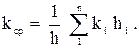(3.20)

Зонально-неоднородный пласт состоит из кольцевых зон. В пределах каждой той зоны (i = 1,2...n) проницаемость постоянна и равна k_i. Наружный и внутренний радиусы зоны равны соответственно R_i, R_i-1. Причем, внутренний радиус первой зоны равен радиусу скважины R_o = r_c, давление жидкости на этой границе равно давлению на скважине p_o = p_c. Наружный радиус последней зоны равен радиусу контура питания R_n = R_k, а давление на нем р_n = p_k.

При движении жидкости к скважине в зонально-неоднородном пласте, дебит в любом поперечном сечении