Выражение отношения в процентах

Методический комментарий

В центре изучения материала данного пункта находится задача: определить, сколько процентов одна величина составляет от другой. Принят подход, в соответствии с которым сначала находим, какую часть одна величина составляет от другой, а затем эту часть выражаем в процентах. Поэтому важно акцентировать внимание на двух моментах: повторить решение задач, рассмотренных в начале года (п. 1.4 учебника, задачи типа 65—67), и отработать умение перейти от десятичной и обыкновенной дроби к процентам (упражнения 533—536).

Решение задач 537—543 целесообразно проводить в два этапа: выразить часть (долю) величины дробью и выразить дробь в процентах.

При решении задач 544 и 545, а также задач 550 и 551 рекомендуется сделать проверку ответа составлением и решением обратной задачи. Например, решив задачу 551 «а», получим ответ: цена акции снизилась на 20%. Теперь можно составить и решить такую задачу: «В сентябре акция стоила 250 р., а в октябре её цена снизилась на 20%. Какой стала цена акции в октябре?»

Значительное внимание уделяется заданиям на прикидку, нацеленным на выработку «ощущения» процента как определённой доли величины (упражнения 546—549).

Комментарий к упражнениям

536. В данном примере перейти от обыкновенной дроби к десятичной целесообразно, используя основное свойство дроби.

537. Для ответа на вопрос задачи следует сначала ответить на вопрос: «Какую часть ...?»

544, 545. Первый вопрос: «На какую часть ...?»; второй: «На сколько процентов ...?».

548. Рассуждать можно так: а) заштрихованная часть чуть больше четверти круга и значительно меньше его половины, т. е. ответом может быть Б — 27%; г) заштрихована треть фигуры, т. е. примерно 33%, — ответ Б;
е) заштриховано менее 50% круга, т. е. надо выбрать ответ В — 45%.

551. Требует внимания выбор величины, по отношению к которой вычисляется, сколько процентов составляет повышение или понижение цены.

554. Можно организовать работу по группам, а затем объединить полученные результаты.

Глава 7. Симметрия (8 уроков)

Примерное поурочное планирование учебного материала

Пункт учебника	Число уроков	Рабочая тетрадь	Характеристика основных видов деятельности учащихся
7.1. Осевая симметрия		47—50 (с. 74—76)	Распознаватьплоские фигуры, симметричные относительно прямой. Вырезать из бумаги две фигуры, симметричные относительно прямой. Строитьс помощью инструментов фигуру (отрезок, ломаную, треугольник, прямоугольник, окружность), симметричную данной относительно прямой, изображатьот руки. Проводитьпрямую, относительно которой две фигуры симметричны.Конструироватьорнаменты и паркеты, используя свойство симметрии. Формулировать свойства двух фигур, симметричных относительно прямой. Исследоватьсвойства фигур, симметричных относительно плоскости, используя эксперимент, наблюдение, моделирование. Описыватьих свойства
7.2. Ось симметрии фигуры		51—56 (с. 77—78), 79, 80 (с. 87), 94 (с. 96)	Находитьв окружающем мире плоские и пространственные симметричные фигуры. Распознаватьфигуры, имеющие ось симметрии. Вырезать их из бумаги,изображатьот руки и с помощью инструментов. Проводитьось симметрии фигуры. Формулироватьсвойства равнобедренного и равностороннего треугольников, прямоугольника, квадрата, круга, связанные с осевой симметрией. Формулироватьсвойства параллелепипеда, куба, конуса, цилиндра, шара, связанные с симметрией относительно плоскости. Конструироватьфигуры, используя свойство симметрии, в том числе с помощью компьютерных программ
7.3. Центральная симметрия		57—65 (с. 79—81)	Распознаватьплоские фигуры, симметричные относительно точки. Строитьфигуру, симметричную данной относительно точки, с помощью инструментов, достраивать, изображатьот руки. Находить центр симметрии фигуры, конфигурации. Конструироватьорнаменты и паркеты, используя свойство симметрии, в том числе с помощью компьютерных программ.Формулировать свойства фигур, симметричных относительно точки.Исследоватьсвойства фигур, имеющих ось и центр симметрии, используя эксперимент, наблюдение, измерение, моделирование. Выдвигатьгипотезы, формулировать, обосновывать, опровергать с помощью контрпримеров утверждения об осевой и центральной симметрии фигур
Обзор и контроль

Основные цели: дать представление о симметрии в окружающем мире; познакомить с основными видами симметрии на плоскости и в пространстве; приобрести опыт построения симметричных фигур; расширить представления об известных фигурах, познакомив со свойствами, связанными с симметрией; показать возможности использования симметрии при решении различных задач и построениях.

Обзор главы.В главе рассматриваются осевая и центральная симметрия, а также примеры симметрии в пространстве.

Изучение осевой и центральной симметрии строится по одной и той же схеме: в ходе физического действия вводится понятие точек, симметричных относительно прямой (центра); анализируются особенности их расположения относительно оси (центра) симметрии и на основе этого формулируется способ построения симметричных точек; рассматриваются фигуры, симметричные относительно прямой (точки), и фиксируется факт их равенства; вводится понятие оси (центра) симметрии фигуры; устанавливается наличие у известных фигур осей (центра) симметрии.

Изучение видов симметрии и её свойств опирается на фактические действия и физический эксперимент. Для осевой симметрии — это перегибание по оси симметрии, для центральной — поворот на 180°.

Являясь основным средством формирования представлений о симметрии, эти действия должны быть постоянной составляющей всех уроков.

Так, введение понятия точек, симметричных относительно прямой (точки), должно сопровождаться практическими действиями, описанными в учебнике (с. 145, 149). Точно так же с помощью реально выполненного наложения учащиеся должны убедиться в равенстве симметричных фигур. (Для этого удобно перенести рисунок на кальку и выполнить перегибание или поворот на 180°.) К опытной проверке целесообразно прибегать и для того, чтобы подтвердить или опровергнуть вывод, к которому пришёл ученик в результате мысленных действий. Так, например, чтобы убедиться, что треугольники в задаче560 несимметричны, можно перенести рисунок на кальку и выполнить перегибание по заданной прямой.

Одно из основных умений, которым должны овладеть учащиеся, — это построение фигуры (точки, отрезка, треугольника и др.), симметричной данной. Заметим, что наряду с обучением построению симметричных фигур по точкам с помощью инструментов следует стремиться к тому, чтобы учащиеся могли представить симметричный образ целиком, нарисовать его от руки. Подчеркнём, что при построении симметричных точек учащиеся имеют право пользоваться любыми инструментами. Что же касается построений циркулем и линейкой, то их надо рассматривать как дополнительный материал, с которым целесообразно ознакомить сильных учащихся.

Обращаем внимание учителя на то, что из двух видов симметрии — осевой и центральной — бо2льшую сложность для усвоения представляет центральная симметрия. В связи с этим к обязательным результатам обучения не отнесено умение построить фигуру, симметричную данной относительно центра. Основная цель изучения данного материала — сформировать представление о центральной симметрии как о повороте на 180°. В связи с этим необходимо убедиться, что учащиеся понимают оборот речи «поворот на 180°» и могут этот поворот выполнить. При повороте на 180° точка занимает положение, противоположное относительно центра, т. е. она оказывается на той же прямой (проходящей через неё и через центр), но по другую сторону от центра.

Полезно, чтобы учащиеся поэкспериментировали с различными центрально-симметричными фигурами. Например, можно начертить в тетради прямоугольник, провести его диагонали и убедиться, что точки их пересечения — центр симметрии прямоугольника. Для этого надо перевести рисунок на кальку, закрепить его в точке пересечения диагоналей и повернуть прямоугольник на кальке вокруг этой точки на 180°. Оба прямоугольника опять совместятся. Далее следует обсудить, какие вершины при этом повороте совместились, какие стороны, углы и т. д.

Среди фигур, с которыми экспериментируют учащиеся, должен быть и равносторонний треугольник. Путём перегибаний учащиеся могут убедиться, что у него три оси симметрии. Если перегибания будут выполнены аккуратно, то учащиеся получат точку пересечения осей симметрии. Здесь же можно убедиться, что эта точка не является его центром симметрии.

Материалы для контроля.

Пособие «Контрольные работы». Проверочные работы: 5. Осевая симметрия; 6. Центр и ось симметрии фигуры.

Осевая симметрия

Комментарий к упражнениям

560. Можно перенести рисунок на кальку и выполнить перегибание.

562. Напоминаем, что на клетчатой бумаге построения выполняются с использованием её свойств.

567. При выполнении задания можно воспользоваться зеркалом.

569. Попросите учащихся сначала объяснить, как должна проходить ось симметрии относительно двух симметричных точек.

570. Наиболее быстрым будет то окрашивание, при котором после первого перегибания получатся 2 окрашенных квадрата, после второго — 4, после третьего — 8, а четвёртое будет последним — окажутся окрашенными все 16 квадратов. Один из возможных вариантов окраски изображён на рисунке 8. (Число внутри квадрата показывает, в результате какого перегибания квадрат оказался окрашенным.)

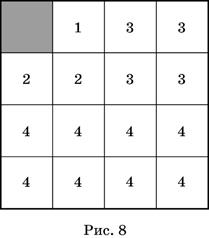
При желании ответ можно получить с помощью эксперимента. Для этого на отдельном листе бумаги нужно воспроизвести рисунок и закрасить чёрный квадрат очень мягким карандашом.

Ось симметрии фигуры

Комментарий к упражнениям

581. Ответ целесообразно проиллюстрировать перегибанием вырезанного из бумаги равностороннего треугольника.

584.У треугольника — 3, у четырёхугольника — 4, у пятиугольника — 5,
у шестиугольника — 6 и т. д.

586, 587.При выполнении заданий учащиеся могут воспользоваться зеркалом.

588. Начать решение надо с рассмотрения рисунка 7.14 учебника. Из рисунка видно, что вершина, не принадлежащая основанию, лежит на оси симметрии треугольника.

Последовательность построений будет такой: строится отрезок, равный
6 см; через его середину проводится прямая, перпендикулярная этому отрезку; на этой прямой выбирается любая точка и соединяется с концами отрезка. Построение может быть выполнено с помощью любых инструментов, а также на клетчатой бумаге с использованием её свойств.

589. Сначала с помощью двух перегибаний получаем две перпендикулярные прямые. Третьим перегибанием нужно загнуть образовавшийся прямой угол. Развернув лист бумаги, мы увидим четыре равнобедренных треугольника, один из которых надо обвести карандашом. Полезно отметить его равные стороны и равные углы.

591.У первого тела две плоскости симметрии, у второго — одна, у третьего — ни одной, у четвёртого — одна.

Центральная симметрия

Комментарий к упражнениям

598. Если в каких-то случаях учащимся проще построить точку, симметричную относительно заданной точки, не по клеткам, а с помощью линейки, они могут это сделать.

601. Учащимся, возможно, будет проще выполнять построения, если они обозначат вершины фигуры буквами.

607. Можно воспользоваться рисунками из этой главы учебника.

Глава 8. Выражения, формулы, уравнения (15 уроков)

Примерное поурочное планирование учебного материала

Пункт учебника	Число уроков	Дидактические материалы	Характеристика основных видов деятельности учащихся
8.1. О математическом языке		О-44, П-34	Обсуждать особенности математического языка. Записывать математические выражения с учётом правил синтаксиса математического языка, составлять выражения по условиям задач с буквенными данными. Использовать буквы для записи математических предложений, общих утверждений; осуществлятьперевод с математического языка на естественный язык и наоборот. Иллюстрировать общие утверждения, записанные в буквенном виде, числовыми примерами
8.2. Буквенные выражения и числовые подстановки		—	Строить речевые конструкции с использованием новой терминологии (буквенное выражение, числовая подстановка, значение буквенного выражения, допустимые значения букв). Вычислятьчисловые значения буквенных выражений при данных значениях букв. Находить допустимые значения букв в выражении. Отвечать на вопросы задач с буквенными данными, составляя соответствующие выражения
8.3. Формулы. Вычисления по формулам		О-45, П-35, П-36	Составлятьформулы, выражающие зависимости между величинами, в том числе по условиям, заданным рисунком. Вычислять по формулам, выражать из формулы одну величину через другие
8.4. Формулы длины окружности, площади круга и объёма шара			Находить экспериментальным путёмотношение длины окружности к диаметру. Обсуждатьособенности числа π; находитьдополнительнуюинформацию об этом числе. Знакомитьсяс формулами длины окружности, площади круга, объёма шара; вычислять по этим формулам. Вычислять размеры фигур, ограниченных окружностями и их дугами. Округлятьрезультаты вычислений по формулам
8.5. Что такое уравнение		О-46, «Проверь себя», П-37	Строить речевые конструкции с использованием слов «уравнение», «корень уравнения». Проверять, является ли указанное число корнем рассматриваемого уравнения. Решатьуравнения на основе зависимостей между компонентами действий. Составлятьматематические модели (уравнения) по условиям текстовых задач
Обзор и контроль

Основные цели: развить представления учащихся об использовании буквенной символики, сформировать элементарные навыки составления буквенных выражений и вычисления их значений, а также работы с формулами, дать первоначальное представление об уравнении с одной переменной.

Обзор главы. Глава включает материал, относящийся к алгебраическому блоку содержания курса математики 5—6 классов. Он группируется вокруг трёх фундаментальных алгебраических понятий: выражение, формула, уравнение. Изложение материала ведётся на основе знакомства с математическим языком, перевода с естественного языка на математический, использования математического языка для описания реальной действительности.

Вначале обсуждается вопрос об использовании букв для обозначения чисел, вводится понятие буквенного выражения и такие связанные с ним понятия, как «числовая подстановка», «значение буквенного выражения», «допустимые значения букв». На элементарном уровне отрабатываются соответствующие практические умения.

Опыт работы с буквенными выражениями является основой для изучения следующего фрагмента, в котором рассматривается вопрос о формулах. Формула для учащихся — это буквенное равенство, которое на символическом языке описывает некоторое правило. Учащиеся записывают в виде формул известные им правила вычисления некоторых величин (периметра и площади прямоугольника и квадрата, объёма прямоугольного параллелепипеда и т. д.) и знакомятся с новыми геометрическими понятиями и соответствующими формулами (длины окружности, площади круга, объёма шара).

Завершается глава обсуждением вопроса об уравнениях. Уравнение появляется как результат перевода условия текстовой задачи на математический язык. Решаются уравнения на этом этапе изучения курса известным из начальной школы приёмом — на основе зависимости между компонентами действий. Подчеркнём, что этот фрагмент по своей дидактической роли служит вводным этапом в тему «Уравнения», изучение которой будет начато в курсе алгебры 7 класса.

Материалы для контроля.

Пособие «Контрольные работы». Зачёт 7. Буквы и формулы.

Пособие «Тематические тесты». Тест 14. Буквы и формулы.

О математическом языке

Методический комментарий

Учащиеся уже имеют опыт использования букв для записи простейших выражений, свойств арифметических действий, для обозначения неизвестного числа. Они также умеют пользоваться такими математическими символами, как знаки арифметических действий, знаки сравнения, скобки. Теперь эти знания и умения служат основой для разговора о математическом языке как специальном языке науки, который создавался и совершенствовался вместе с развитием математики.

Упражнения в пункте направлены на формирование навыков чтения и записи буквенных выражений и буквенных равенств. Вся работа осуществляется как деятельность по переводу с естественного языка на математический и наоборот. К системе упражнений учебника целесообразно добавить задания на содержательную интерпретацию буквенных выражений, например: «Килограмм шоколадных конфет стоит а рублей, килограмм карамели стоит b рублей. Что могло быть куплено, если стоимость покупки (в рублях) равна a + b? 3b? 2a? 2a + b? Каков смысл выражения a – b?»

Комментарий к упражнениям

618. Выражения следует записывать с учётом правил, изложенных в
теоретической части пункта.

619. а) Ученики могут дать ответ в виде а · 2. После этого надо перейти к принятой форме записи: а · 2 = 2а.

б) Возможны разные варианты ответа: 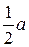, а : 2, .

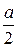г) Типичная ученическая ошибка: ответ записывается в виде 10% а. Ученики должны осознать необходимость выражения процентов числом: 10% — это 0,1. Тогда задание сводится к вариантам «а»—«в».

622. В заданиях «а»—«г» достаточно подобрать какое-то число, при котором записанное буквенное неравенство обращается в верное числовое неравенство. В случае «д» такое число единственное: х + 15 = 31, если х = 16. Учащиеся просто должны дать ответ, говорить о решении уравнения здесь не надо. В сильном классе подобное задание можно предложить для случаев «е» и «ж».

625. Каждое следующее натуральное число на 1 больше предыдущего. Если произвольное натуральное число обозначить буквой n, то следующее число нужно записать как n + 1.

а) n(n + 1); б) n + (n + 1).