Округление натуральных чисел

Методический комментарий

Данный вопрос, как и любой другой, связанный с приближёнными вычислениями, относится к темам, которые наиболее трудны для восприятия учащимися. Основной целью данного этапа является создание первоначальных представлений, необходимых для формирования оценочных умений, выполнения заданий на прикидку и оценку результата.

Термин «округление» отождествляется с заменой первоначального числа круглым, т. е. числом с нулями на конце. Округление вначале осуществляется на содержательном уровне, по смыслу: из двух круглых чисел, между которыми заключено данное число, выбирается то, к которому оно ближе. Например, 560 < 564 < 570, и число 564 ближе к 560, чем к 570. Поэтому 564 ≈ 560 (здесь мы округлили число 564 до десятков).

После того как будет выполнено несколько заданий на округление чисел по смыслу, следует предложить учащимся правило округления, которое позволяет действовать формально, без реального или мысленного обращения к координатной прямой, без предварительной оценки заданной величины снизу и сверху круглыми числами.

Учащимся легче будет запомнить и применять правило округления натуральных чисел, если их убедить в его естественности и разумности. Это можно сделать, обратившись сначала к рассмотренным выше примерам округления до десятков чисел 564, 565, 568 (см. с. 38 учебника):

564 ≈ 560, 565 ≈ 570, 568 ≈ 570.

Беседа может быть такой. Посмотрите: при округлении до десятков цифра в разряде десятков либо не менялась, либо увеличилась на 1. В каком случае она не менялась? А какие ещё числа вместо 564 можно было бы взять, чтобы эта цифра также осталась неизменной? А в каких случаях в разряде десятков вместо цифры 6 оказалась цифра 7? А если бы мы округляли до десятков число 566, какой стала бы цифра в разряде десятков? После этого можно обратиться к первому пункту правила округления.

Познакомив учащихся с правилом округления, можно предложить в дальнейшем действовать так, как им удобнее. При этом всё же следует подчеркнуть, что с помощью правила числа округлять легче.

В заключение заметим, что на этом этапе не стоит значительно увеличивать число упражнений на округление чисел, включать трудные случаи. К этому вопросу можно будет вернуться при изучении десятичных дробей в 6 классе.

Комментарий к упражнениям

121. Аналогичные задания:

1) Масса искусственного спутника Земли 1327 кг. Сколько это примерно тонн?

2) Длина реки Лены 4400 км. Если выразить эту величину в тыс. км, то получим 4 тыс. км. Выразите в тыс. км длину реки Енисея – 3487 км, реки Оби – 3650 км.

124. Дополнительный вопрос: какие ещё употребляют слова при изложении подобного рода информации? Приведите свои примеры.

130. В школе от 600 до 800 учащихся. Если в школе 758 учеников, то число 800; если 626, то число 600.

131. Нужно рассмотреть два случая: 1) при округлении цифра в разряде десятков не менялась; 2) цифра в разряде десятков в результате округления увеличивалась на 1.

Решение комбинаторных задач

Методический комментарий

В пункте представлены комбинаторные задачи на размещения, сочетания, перестановки с повторением и без повторения элементов. Однако ни сами эти термины, ни соответствующие формулы не рассматриваются. Используется естественный, доступным детям этого возраста метод решения комбинаторных задач с помощью непосредственного перебора возможных вариантов (комбинаций). Этот метод целесообразен в тех случаях, когда число вариантов невелико.

На первоначальном этапе освоения решить комбинаторную задачу — это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и т. д., отвечающих условию задачи. Цель пункта состоит в том, чтобы в процессе решения системы задач учащиеся встретились с необходимостью перебора различных по своей сути и составу комбинаций.

При решении каждой задачи ставится один и тот же вопрос: как организовать перебор вариантов, чтобы не пропустить ни один из них и в то же время избежать повтора?

Среди других способов перебора в теоретической части пункта предлагается осуществление перебора с помощью специальной схемы — дерева возможных вариантов. Желательно, чтобы построение дерева выполнялось без использования линейки.

Решение комбинаторных задач считается правильным и полным, если учащийся предъявил все возможные варианты, каким бы способом решения он при этом ни воспользовался.

Упражнения группы А по сути являются аналогами задач, рассмотренных в тексте, в них применяются те же схемы рассуждений. Так, упражнения 137и 138 — это вариации на тему задачи 1; упражнения 139—142 решаются с помощью такого же приёма, что и задача 2; упражнения 143 и 144 — это задания на перестановки, как и задача 3 из текста учебника; наконец, упражнения 145—147 выполняются с помощью построения дерева возможных вариантов (см. конец теоретической части пункта). Что касается упражнений группы Б, то все они разные, в них представлены некоторые новые идеи.

Комментарий к упражнениям

137. Всего получается 16 чисел:

33, 35, 37, 39,

53, 55, 57, 59,

73, 75, 77, 79,

93, 95, 97, 99.

Если использовать каждую цифру только один раз, то из приведённого списка надо вычеркнуть числа 33, 55, 77, 99. Останется 12 чисел.

138. Прежде всего, заметим, что число не может начинаться с цифры 0. Далее возможны два варианта решения задачи.

Можно выписать числа 10, 12, 20, 21, сразу отбросив не устраивающие нас числа 11 и 22.

А можно записать все возможные двузначные числа, состоящие из данных цифр в порядке возрастания: 10, 11, 12, 20, 21, 22, и потом вычеркнуть числа 11 и 22, состоящие из одинаковых цифр. После чего получим 4 числа: 10, 12, 20, 21.

Соответственно, если каждую цифру можно использовать не один раз, то получится 6 чисел.

139. Обозначим полицейских первыми буквами их фамилий: Б, С, У, Д. Далее рассуждаем по той же схеме, что и в задаче об отрезках на прямой (см. задачу 2). Сначала выпишем все пары, в которые входит буква Б; получим БС, БУ, БД. Теперь запишем пары, в которые входит буква С. Пару СБ отбрасываем, так как в неё входят те же два полицейских, что и в пару БС. Получаем СУ, СД. Рассуждая так же, находим ещё пару УД. Всего получаем 6 способов составления пар полицейских.

140. Ввести обозначения: Ш, Л, К, Э. Далее рассуждать так же, как в задаче 2. Всего 6 способов.

141. Каждой из книг присвоим номер от 1 до 5; получим 1, 2, 3, 4, 5. Далее рассуждаем, как в задачах выше.

143. Можно рассуждать так: два возможных шифра начинаются с цифры 1, два шифра — с цифры 2 и два шифра — с цифры 3. Итого 6 шифров: 123, 132, 213, 231, 312, 321.

145. Обозначим возможные виды транспорта соответствующими буквами (например, теплоход — буквой Т). Дерево возможных вариантов имеет следующий вид:

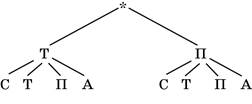
Всего 8 способов.

148. 1-й способ. Можно записать числа в порядке возрастания:

444, 445, 454, 455,

544, 545, 554, 555.

Получим 8 чисел.

2-й способ. Можно нарисовать дерево возможных вариантов:

Всего получается 8 чисел.

149. Запишем все такие числа в порядке возрастания: I, II, III, IV, V, VI, VII, VIII. Для следующих чисел уже нужны другие цифры. Всего получим 8 чисел.

150. Понятно, что эти числа должны начинаться с цифры 4. Цифру 4 на первом месте «фиксируем», а цифры в остальных трёх разрядах получаются всеми возможными перестановками цифр 1, 2 и 3 (см. упражнение 143). Получаем 6 чисел: 4123, 4132, 4213, 4231, 4312, 4321.

151. Рассуждаем по той же схеме, что и в задаче 2. Сначала вычёркиваем все возможные пары цифр, в которые входит цифра 4. Вычеркнули 4 и 8, получили 5203; вычеркнули 4 и 5, получили 8203; вычеркнули 4 и 2, получили 8503; вычеркнули 4 и 0, получили 8523; вычеркнули 4 и 3, получили 8520.

Далее вычёркиваем все возможные пары, в которые входит цифра 8. Пара из цифр 8 и 4 уже рассматривалась. Вычёркиваем пары 8 и 5, 8 и 2, 8 и 0,
8 и 3; получаем ещё четыре числа: 4203, 4503, 4523, 4520. Рассуждая так же, получаем числа: 4803, 4823, 4820; 4853, 4850; 4852. Всего 15 чисел.

Самое большое число – это 8523.

152. Искомые двузначные числа могут начинаться с любой цифры,
кроме 0. С цифры 1 начинается одно такое число – это 10; с цифры 2 начинаются два таких числа – это 20 и 21; с цифры 3 начинаются три таких числа – это 30, 31, 32, и т. д.

Всего имеем 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 чисел.

153.Комбинации можно описать с помощью наборов из пяти цифр, причём на первом месте всегда стоит 1, а на последнем — цифра 5. Фактически нужно определить число всех возможных троек, которые можно составить из цифр 2, 3 и 4. Всего имеется 6 вариантов передачи шайбы (включая изображённую на рисунке): 12345, 12435, 13245, 13425, 14235, 14325.

154. Введём краткие обозначения для предметов: Р, Б, З, А. Выпишем все возможные пары, составленные из двух разных предметов: РБ, РЗ, РА, БЗ, БА, ЗА. Всего имеется 6 таких пар. Значит, 10 различных выигрышей составить нельзя.